解题思路
一:题目
4用电压V=10v的电池给电容充电,电容上t时刻的电压为v(t)= ,其中V0是电容的初始电压,
,其中V0是电容的初始电压,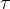 是充电常数,是由下列数据确定V0和
是充电常数,是由下列数据确定V0和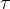 。
。
| t/s | 0.5 | 1 | 2 | 3 | 4 | 5 | 7 | 9 |
| v/V | 6.36 | 6.48 | 7.26 | 8.22 | 8.66 | 8.99 | 9.43 | 9.63 |
二:思路
根据所给的数据,使用分析函数的特征使用插值与拟合方法来,获得函数图像与函数表达式,并评估模型的接近程度,从而带入参数获得V0和
开发环境
vscode python
代码及效果
一:代码
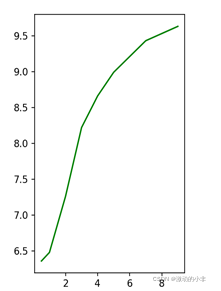 从图分析可知,函数为非线性函数,从表达式佐证v一阶导数,不为常数,为多项式,故在此使用非线性最小二乘法拟合数据,得到局部最优解。
从图分析可知,函数为非线性函数,从表达式佐证v一阶导数,不为常数,为多项式,故在此使用非线性最小二乘法拟合数据,得到局部最优解。
代码示例:
from tkinter.font import families
import numpy as np
from scipy.optimize import curve_fit
import pylab as plt
#变量的范围
t=np.array([0.5,1,2,3,4,5,7,9])
v=np.array([6.36,6.48,7.26,8.22,8.66,8.99,9.43,9.63])
#函数表达式
def fun(t,v0,a):#t传入的变量,v0,a拟合参数。
return 10-(10-v0)*np.exp(-t/a)
popt,pcov=curve_fit(fun,t,v)#最小二乘法拟合
print('v0,a充电常数字',popt)
yh2=fun(t,*popt)#计算已经知道数据的预测值
plt.rc('font',family='SimHei')
plt.rc('font',size=16)
plt.plot(t,v,'o')#画出拟合函数
plt.plot(t,yh2)#画出数据点
plt.legend(['data','fun'])
plt.show()
二:效果
效果
v0,
充电常数字 [5.55766614 , 3.50019433]
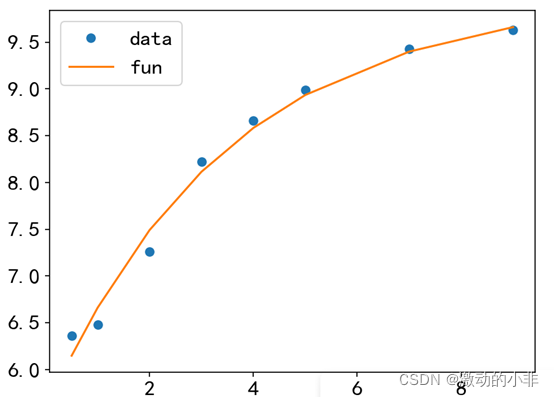









 该博客通过分析给定的电容充电电压数据,运用非线性最小二乘法进行曲线拟合。利用Python的`scipy.optimize.curve_fit`函数,博主成功地拟合了数据并得到了电容初始电压V0和充电常数a的值。代码展示了一个从数据到模型建立的过程,最终得出V0约为5.56V,a约为3.50的时间常数。博客中还展示了拟合后的图表,显示了实际数据点与拟合曲线的良好吻合。
该博客通过分析给定的电容充电电压数据,运用非线性最小二乘法进行曲线拟合。利用Python的`scipy.optimize.curve_fit`函数,博主成功地拟合了数据并得到了电容初始电压V0和充电常数a的值。代码展示了一个从数据到模型建立的过程,最终得出V0约为5.56V,a约为3.50的时间常数。博客中还展示了拟合后的图表,显示了实际数据点与拟合曲线的良好吻合。
















 4727
4727

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








