离散时间系统
1 定义
- 离散系统将一个序列转换、映射成另一个序列。
- 系统三要素:
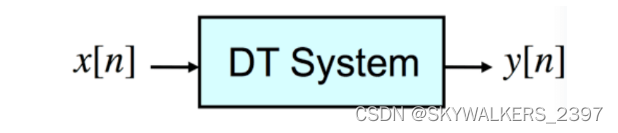
- 输入: x [ n ] x[n] x[n]
- 输出: y [ n ] y[n] y[n]
- 输入与输出关系: y [ n ] = f ( x [ n ] ) , ∀ n y[n] = f(x[n]),\forall n y[n]=f(x[n]),∀n
2 基本离散时间系统
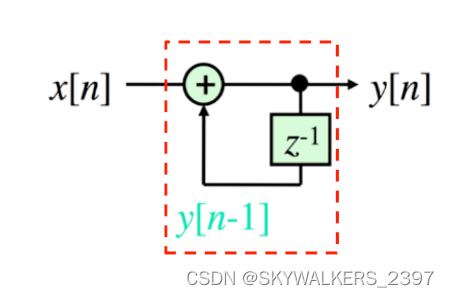
(1) 累加器:输出是当前时刻之前所有输入之和
y
[
n
]
=
∑
l
=
−
∞
n
x
[
j
]
=
∑
l
=
−
∞
n
−
1
x
[
j
]
+
x
[
n
]
=
y
[
n
−
1
]
+
x
[
n
]
y[n] = \sum_{l=-\infty}^n x[j] = \sum_{l=-\infty}^{n-1} x[j] + x[n] = y[n-1] + x[n]
y[n]=l=−∞∑nx[j]=l=−∞∑n−1x[j]+x[n]=y[n−1]+x[n]
(2) 滑动平均滤波器

y [ n ] = 1 M ∑ l = 0 M − 1 x [ n − l ] y[n] = \frac 1 M \sum_{l = 0}^{M - 1}x[n-l] y[n]=M1l=0∑M−1x[n−l]
- 滑动平均滤波器可消除信号的急剧变化,如噪声:
x [ n ] = s [ n ] + d [ n ] x[n] = s[n] + d[n] x[n]=s[n]+d[n]
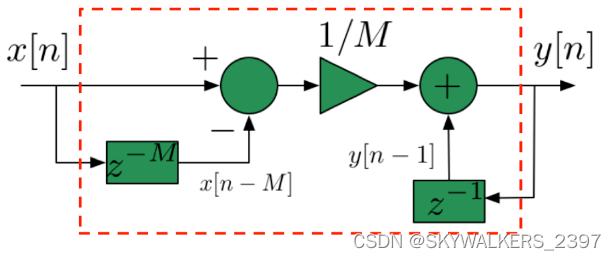
y [ n ] = 1 5 ∑ k = 0 4 x [ n − k ] y[n] = \frac 1 5 \sum_{k=0}^4 x[n-k] y[n]=51k=0∑4x[n−k] - 快速形式
 y
[
n
]
=
1
M
∑
l
=
0
M
−
1
x
[
n
−
l
]
=
1
M
(
∑
l
=
0
M
−
1
x
[
n
−
l
]
+
x
[
n
−
M
]
−
x
[
n
−
M
]
)
=
1
M
(
∑
l
=
1
M
x
[
n
−
l
]
+
x
[
n
]
−
x
[
n
−
M
]
)
=
y
[
n
−
1
]
+
1
M
(
x
[
n
]
−
x
[
n
−
M
]
)
y[n] = \frac 1M \sum_{l = 0}^{M - 1}x[n-l] = \frac 1M (\sum_{l = 0}^{M - 1}x[n-l] + x[n-M] - x[n-M]) \\ = \frac 1M (\sum_{l = 1}^{M}x[n-l] + x[n] - x[n-M]) = y[n-1] + \frac1M (x[n] - x[n-M])
y[n]=M1l=0∑M−1x[n−l]=M1(l=0∑M−1x[n−l]+x[n−M]−x[n−M])=M1(l=1∑Mx[n−l]+x[n]−x[n−M])=y[n−1]+M1(x[n]−x[n−M])
y
[
n
]
=
1
M
∑
l
=
0
M
−
1
x
[
n
−
l
]
=
1
M
(
∑
l
=
0
M
−
1
x
[
n
−
l
]
+
x
[
n
−
M
]
−
x
[
n
−
M
]
)
=
1
M
(
∑
l
=
1
M
x
[
n
−
l
]
+
x
[
n
]
−
x
[
n
−
M
]
)
=
y
[
n
−
1
]
+
1
M
(
x
[
n
]
−
x
[
n
−
M
]
)
y[n] = \frac 1M \sum_{l = 0}^{M - 1}x[n-l] = \frac 1M (\sum_{l = 0}^{M - 1}x[n-l] + x[n-M] - x[n-M]) \\ = \frac 1M (\sum_{l = 1}^{M}x[n-l] + x[n] - x[n-M]) = y[n-1] + \frac1M (x[n] - x[n-M])
y[n]=M1l=0∑M−1x[n−l]=M1(l=0∑M−1x[n−l]+x[n−M]−x[n−M])=M1(l=1∑Mx[n−l]+x[n]−x[n−M])=y[n−1]+M1(x[n]−x[n−M])
3 分类
(1) 线性系统
线性系统遵循叠加原理:定义输入
x
1
[
n
]
→
x_1[n] \rightarrow
x1[n]→输出
y
1
[
n
]
y_1[n]
y1[n],
x
2
[
n
]
→
y
2
[
n
]
.
.
.
x_2[n] \rightarrow y_2[n] ...
x2[n]→y2[n]...,若系统输入为以上信号的线性组合:
x
[
n
]
=
α
x
1
[
n
]
+
β
x
2
[
n
]
x[n] = \alpha x_1[n] + \beta x_2[n]
x[n]=αx1[n]+βx2[n],则输出一定满足:
y
[
n
]
=
α
y
1
[
n
]
+
β
y
2
[
n
]
y[n] = \alpha y_1[n] + \beta y_2[n]
y[n]=αy1[n]+βy2[n]。
(2) 时不变系统
时不变系统输入的偏移将导致输出也有同样的偏移:即如果 x 1 [ n ] → y 1 [ n ] x_1[n] \rightarrow y_1[n] x1[n]→y1[n],则一定满足 x [ n ] = x 1 [ n − n 0 ] ⇉ y [ n ] = y 1 [ n − n 0 ] x[n] = x_1[n - n_0] \rightrightarrows y[n] = y_1[n - n_0] x[n]=x1[n−n0]⇉y[n]=y1[n−n0]
时不变系统的以上特性不依赖与n的取值(与输入施加到系统的时刻无关)
线性时不变系统
- 这类系统既满足线性又满足时不变
- 很容易从数学上分析和处理,被广泛使用且非常有用的一类系统
- 线性移不变系统:如果索引为时间,则称为线性时不变系统,反之,则称为线性移不变系统。
(3) 因果系统
如果系统输出仅依赖与过去和现在时刻的输入(与将来的输入无关),在满足这种条件的系统称为因果系统。
即若存在输入输出关系对: x 1 [ n ] → y 1 [ n ] x_1[n]\rightarrow y_1[n] x1[n]→y1[n]且 x 2 [ n ] → y 2 [ n ] x_2[n]\rightarrow y_2[n] x2[n]→y2[n],则因果系统满足: x 1 [ n ] = x 2 [ n ] ∀ n < N ⇔ y 1 [ n ] = y 2 [ n ] ∀ n < N x_1[n] = x_2[n] \forall n<N \Leftrightarrow y_1[n] = y_2[n] \forall n<N x1[n]=x2[n]∀n<N⇔y1[n]=y2[n]∀n<N
(4) 稳定系统
BIBO系统:若x[n]的系统响应是y[n],且对于所有的n值:
∣
x
[
n
]
∣
<
B
x
|x[n]|<B_x
∣x[n]∣<Bx
即输入为有界序列,则对于所有的n值,输出也为有界序列:
∣
y
[
n
]
∣
<
B
y
|y[n]|<B_y
∣y[n]∣<By
线性时不变系统(时域)
冲激响应
(1)定义:
给定一个系统,当输入为冲激函数 δ [ n ] \delta[n] δ[n]时,系统输出为冲激响应h[n]
线性时不变系统完全由冲激响应h[n]确定
(2)输入输出关系:
任意一个序列可表示为基础序列与其延迟或超前版本的加权和:
x
[
n
]
=
∑
k
=
−
∞
∞
x
[
k
]
δ
[
n
−
k
]
x[n] = \sum_{k = -\infty}^{\infty}x[k]\delta[n - k]
x[n]=k=−∞∑∞x[k]δ[n−k]
换一种表示,上式可理解为任意序列x[n]可看作本省与
δ
[
n
]
\delta[n]
δ[n]的卷积
因此对于LTI系统,由y[n] = x[n] * h[n]
(3)系统级联:
若两个系统分别具有冲激响应 h 1 [ n ] h_1[n] h1[n]和 h 2 [ n ] h_2[n] h2[n],则两者级联的冲激响应h[n]为 h [ n ] = h 1 [ n ] ∗ h 2 h[n] = h_1[n]*h_2 h[n]=h1[n]∗h2
(4)逆系统:
考虑:
z
[
n
]
=
h
2
[
n
]
∗
y
[
n
]
=
h
2
[
n
]
∗
h
1
[
n
]
∗
x
[
n
]
z[n] = h_2[n]*y[n] = h_2[n]*h_1[n]*x[n]
z[n]=h2[n]∗y[n]=h2[n]∗h1[n]∗x[n]
如果:
h
2
[
n
]
=
δ
[
n
]
h_2[n] = \delta [n]
h2[n]=δ[n],则称
h
2
[
n
]
h_2[n]
h2[n]是
h
1
[
n
]
h_1[n]
h1[n]的逆系统
(5)系统并联:
两个系统的冲激响应相加就是其并联系统的冲激响应:
h
[
n
]
=
h
1
[
n
]
+
h
2
[
n
]
h[n] = h_1[n] + h_2[n]
h[n]=h1[n]+h2[n]
因果稳定
对于LTI系统:
- 稳定性:冲激响应h[n]满足绝对可和
- 因果性:冲激响应h[n]为因果序列
(1)稳定性条件
- BIBO稳定性:有界输入 ∣ x [ n ] ∣ ⩽ B x < ∞ |x[n]| \leqslant B_x < \infty ∣x[n]∣⩽Bx<∞产生有界输出。
- 充分性:若h[n]满足绝对可和:
∣ y [ n ] ∣ ⩽ ∑ k = − ∞ ∞ ∣ x [ n − k ] ∣ ∣ h [ k ] ⩽ B x ∑ k = − ∞ ∞ ∣ h [ k ] ∣ < ∞ |y[n]| \leqslant \sum_{k = -\infty}^\infty |x[n-k]||h[k]\leqslant B_x \sum_{k = -\infty}^\infty|h[k]|<\infty ∣y[n]∣⩽k=−∞∑∞∣x[n−k]∣∣h[k]⩽Bxk=−∞∑∞∣h[k]∣<∞ - 必要性:反之,若h[n]不满足绝对可和,假设输入 x [ n ] = s i g n ( h [ − n ] ) : x[n] = sign(h[-n]): x[n]=sign(h[−n]):
y
[
0
]
=
∑
k
=
−
∞
∞
∣
x
[
−
k
]
∣
∣
h
[
k
]
∣
=
∑
k
=
−
∞
∞
∣
h
[
k
]
∣
=
∞
y[0] = \sum_{k = -\infty}^\infty |x[-k]||h[k]| = \sum_{k = -\infty}^\infty |h[k]| = \infty
y[0]=k=−∞∑∞∣x[−k]∣∣h[k]∣=k=−∞∑∞∣h[k]∣=∞
其不满足BIBO稳定性条件
(2) 因果性条件
- 假设输入
x
1
[
n
]
,
x
2
[
n
]
x_1[n],x_2[n]
x1[n],x2[n]满足:
x 1 [ n ] = x 2 [ n ] , ∀ n ⩽ n 0 x_1[n] = x_2[n] , \forall n \leqslant n_0 x1[n]=x2[n],∀n⩽n0
x 1 [ n ] ≠ x 2 [ n ] , ∀ n > n 0 x_1[n] \not ={} x_2[n] , \forall n > n_0 x1[n]=x2[n],∀n>n0 - 考虑当
n
=
n
0
n = n_0
n=n0时的输出:
y 1 [ n 0 ] = ∑ k = 0 ∞ h [ k ] x 1 [ n 0 − k ] + ∑ k = − ∞ − 1 h [ k ] x 1 [ n 0 − k ] y_1[n_0] = \sum_{k = 0}^\infty h[k]x_1[n_0-k]+\sum_{k = -\infty}^{-1} h[k]x_1[n_0-k] y1[n0]=k=0∑∞h[k]x1[n0−k]+k=−∞∑−1h[k]x1[n0−k]
y 2 [ n 0 ] = ∑ k = 0 ∞ h [ k ] x 2 [ n 0 − k ] + ∑ k = − ∞ − 1 h [ k ] x 2 [ n 0 − k ] y_2[n_0] = \sum_{k = 0}^\infty h[k]x_2[n_0-k]+\sum_{k = -\infty}^{-1} h[k]x_2[n_0-k] y2[n0]=k=0∑∞h[k]x2[n0−k]+k=−∞∑−1h[k]x2[n0−k] - 因此,可确定冲激响应的因果性:
h [ k ] = 0 , k < 0 h[k] = 0,k<0 h[k]=0,k<0
系统分类
- 基于冲激响应长度
- 有限冲激响应(FIR)
- 无限冲激响应(IIR)
- 基于冲激响应系统
- 实离散时间系统
- 复离散时间系统
- 基于输出计算过程
- 非递归离散时间系统
- 递归离散时间系统
线性时不变系统(频域)
频率响应
(1)定义
一个线性时不变系统对复指数信号的响应也是同样一个复指数信号,不同的只是幅度上的变化。
当输入为复指数时,即
x
[
n
]
=
e
j
ω
0
n
x[n] = e^{j\omega_0n}
x[n]=ejω0n
其输出
y
[
n
]
=
∑
m
h
[
m
]
e
j
ω
0
(
n
−
m
)
=
∑
m
h
[
m
]
e
−
j
ω
0
m
e
j
ω
0
n
=
H
(
e
j
ω
0
)
x
[
n
]
=
∣
H
(
e
j
ω
0
)
∣
e
j
(
ω
0
n
+
θ
(
ω
0
)
)
y[n] = \sum_m h[m]e^{j\omega_0(n-m)} = \sum_m h[m]e^{-j\omega_0m}e^{j\omega_0n} = H(e^{j\omega_0})x[n] = |H(e^{j\omega_0})|e^{j(\omega_0n + \theta(\omega_0))}
y[n]=∑mh[m]ejω0(n−m)=∑mh[m]e−jω0mejω0n=H(ejω0)x[n]=∣H(ejω0)∣ej(ω0n+θ(ω0))
其中 H ( e j ω 0 ) H(e^{j\omega_0}) H(ejω0)被称作LTI离散时间系统的频率响应
(2)实正弦
一个频率为
ω
0
\omega_0
ω0的实正弦信号通过一个具有实冲激函数h[n]的LSI系统,具有增益放缩
∣
H
(
e
j
ω
0
)
∣
|H(e^{j\omega_0})|
∣H(ejω0)∣向往平移
θ
(
ω
0
)
\theta(\omega_0)
θ(ω0)
A
c
o
s
(
ω
0
n
+
ϕ
)
∗
h
[
n
]
=
A
∣
H
(
e
j
ω
0
)
∣
c
o
s
(
ω
0
n
+
ϕ
+
θ
(
ω
0
)
)
Acos(\omega_0n+\phi) * h[n] = A|H(e^{j\omega_0})|cos(\omega_0n+\phi+\theta(\omega_0))
Acos(ω0n+ϕ)∗h[n]=A∣H(ejω0)∣cos(ω0n+ϕ+θ(ω0))
(3)因果指数序列的暂态响应与稳态响应
y
[
n
]
=
x
[
n
]
∗
h
[
n
]
=
∑
m
=
−
∞
n
h
[
m
]
e
j
ω
0
(
n
−
m
)
−
∑
m
=
n
+
1
∞
h
[
m
]
e
j
ω
0
(
n
−
m
)
=
H
(
e
j
ω
0
)
e
j
ω
0
n
−
(
∑
m
=
n
+
1
∞
h
[
m
]
e
−
j
ω
0
m
)
e
j
ω
0
n
y[n] = x[n] * h[n] = \sum_{m = -\infty}^n h[m]e^{j\omega_0(n-m)} - \sum_{m = n + 1}^\infty h[m]e^{j\omega_0(n-m)} = H(e^{j\omega_0})e^{j\omega_0n} - (\sum_{m = n + 1}^\infty h[m]e^{-j\omega_0m})e^{j\omega_0n}
y[n]=x[n]∗h[n]=m=−∞∑nh[m]ejω0(n−m)−m=n+1∑∞h[m]ejω0(n−m)=H(ejω0)ejω0n−(m=n+1∑∞h[m]e−jω0m)ejω0n
暂态响应:
H
(
e
j
ω
0
)
e
j
ω
0
n
H(e^{j\omega_0})e^{j\omega_0n}
H(ejω0)ejω0n,与纯正弦输入相同
稳态响应:
(
∑
m
=
n
+
1
∞
h
[
m
]
e
−
j
ω
0
m
)
e
j
ω
0
n
(\sum_{m = n + 1}^\infty h[m]e^{-j\omega_0m})e^{j\omega_0n}
(∑m=n+1∞h[m]e−jω0m)ejω0n,门控的结果
简单滤波器
- 核心思想:用设计的
H
(
e
j
ω
0
)
H(e^{j\omega_0})
H(ejω0)分离频率信息
如: x [ n ] = A c o s ( ω 1 n ) + B c o s ( ω 2 n ) x[n] = Acos(\omega_1n)+Bcos(\omega_2n) x[n]=Acos(ω1n)+Bcos(ω2n) - 构建一个滤波器
∣
H
(
e
j
ω
1
)
∣
≈
1
|H(e^{j\omega_1})| \approx 1
∣H(ejω1)∣≈1
∣
H
(
e
j
ω
2
)
∣
≈
0
|H(e^{j\omega_2})| \approx 0
∣H(ejω2)∣≈0
则 y [ n ] = h [ n ] ∗ x [ n ] ≈ A c o s ( ω 1 n + θ ( ω 1 ) ) y[n] = h[n] * x[n] \approx Acos(\omega_1n+\theta(\omega_1)) y[n]=h[n]∗x[n]≈Acos(ω1n+θ(ω1))
三点滤波器:
h
[
n
]
=
α
β
α
h[n] = {\alpha ~~~ \beta ~~~ \alpha}
h[n]=α β α
频率响应:
∣
H
(
e
j
ω
0
)
∣
=
∣
β
+
2
α
c
o
s
(
ω
0
)
∣
|H(e^{j\omega_0})| = |\beta+2\alpha cos(\omega_0)|
∣H(ejω0)∣=∣β+2αcos(ω0)∣






















 810
810











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








