通信原理——信道

1 信道的数学模型

一般来说，对于信道有两种不同的定义，调制信道和编码信道，如下图所示：

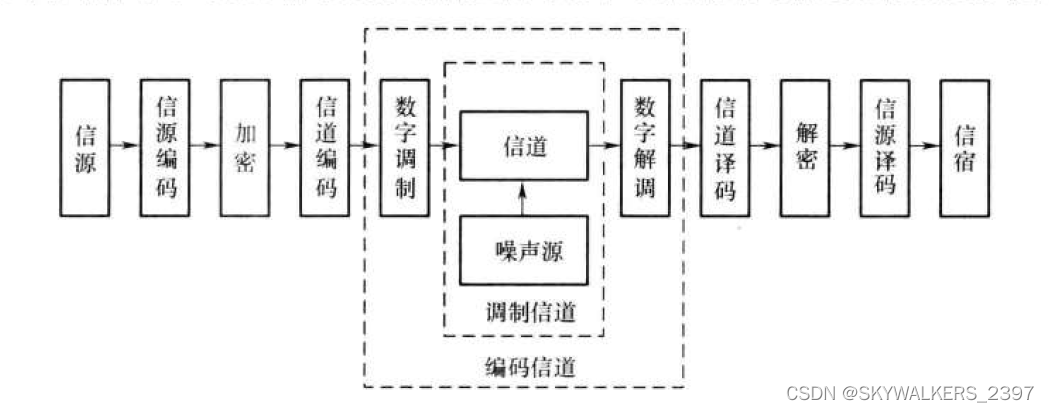
通常，信道一词在研究调制系统时均指调制信道；只有在讨论信道编码时，信道表示编码信道。

1.1 调制信道模型

最基本的调制信道有一对输入端和一对输出端，其输入端信道电压$e_i(t)$和输出端电压$e_o(t)$间的关系可以用下式表示：
$$e_o(t)=f[e_i(t)]+n(t)$$
式中：$n(t)$为噪声电压
由于信道中的噪声是叠加在信号上的，而且无论有无信号，噪声始终存在，因此通常称为加性噪声或加性干扰。$f[e_i(t)]$表示信道输入和输出电压之间的函数关系，通常假设$f[e_i(t)]=k(t)e_i(t)$，即信道的作用相当于对输入信号乘一个系数，即：
$$e_o(t)=k(t)e_i(t)+n(t)$$
上式就是调制信道的一般数学模型，图形表示如下：

一般来说，$k(t)$是时间t的函数，随时间变换的信道称为时变信道。$k(t)$也可以看作是对信号的一种干扰，称为乘性干扰。作为一种干扰，会使信号产生各种失真。这些失真都可能随时间做随机变换。这种特性随机变化的信道称为随机参量信道，简称随参信道。另外，也有些信道的特性基本不随时间变换，这种信道称为恒定参量信道，简称恒参信道。

1.2 编码信道模型

由于编码信道对信号的输入输出是数字序列，故编码信道对信号的影响是使传输的熟悉序列发生变化，即序列中的数字发生错误。所以，可以用转移概率来描述编码信道的特性。一个二进制编码信道的简单模型如下：

图中$P(0/0)和P(1/1)$是正确转移概率。$P(1/0)$是发送“0”而接收“1”的概率；$P(0/1)$是发送“1”而接收“0”的概率。后面两个概率为错误传输概率。

2 信道特性对信号传输的影响

恒参信道的主要传输特性通常可以用其振幅——频率特性和相位——频率特性来描述。若信道的振幅——频率特性不理想，则信号发生的失真称为频率失真。信号的频率失真会使信号的波形产生畸变。在传输数字信号时，会引起码间串扰。若信道的相位——频率特性不理想将使信号产生相位失真。
除此之外，恒参信道还存在其他使信号产生失真的因素，例如非线性失真、频率偏移和相位抖动等。非线性特性将使信号产生新的谐波分量，造成谐波失真，主要是由于信道中的元器件特性不理想造成的。频率偏移是指信道输入信号的频谱经过信道传输后产生了平移。主要是因为发送端和接收端中用于调制解调或频率变换的振荡器的频率误差引起的。相位抖动也是由于这些振荡器的频率不稳定产生的。

3 信道中噪声

信道中的噪声可分为：

• 加性噪声、乘性噪声
• 白(色)噪声、有色噪声

信道中加性噪声的来源的不同，—般分为：

• 无线电噪声：它来源于别的无线电发射机。
• 工业噪声：来源于各种电气设备。
• 自然噪声（天电噪声），指自然界存在的各种电磁波源。
• 内部噪声。内部噪声是系统设备本身产生的各种噪声。

按随机噪声的性质进行分类，可分为：

• 单频噪声：是一种连续波的干扰(如外台信号)，主要特点是占有极窄的频带，但在频率轴上的位置可以实测。
• 脉冲噪声：是在时间上无规则地突发的短促噪声，但持续时间短。从频谱上看，脉冲噪声通常有较宽的频谱(从甚低频到高频)，但频率越高，其频谱强度就越小。
• 起伏噪声：以热噪声、散弹噪声及宇宙噪声为代表的噪声。特点是，无论在时域内还是在频域内它们总是普遍存在和不可避免的。

热噪声：导体中，自由电子的布朗运动引起的噪声。服从高斯分布，可以证明，自由电子电流的功率密度谱为：
$$Pi(\omega )=\frac{2kTG}{1+{(\omega /a)}^2}$$

4 信道容量

信息容量：单位时间内信道上所能传输的最大信息量。

4.1 离散信道容量

离散信道容量有两种不同的度量单位，一种是用每个符号能够传输的平均信息量最大值表示信道容量C:
C = max ⁡ { p ( x ) } [ H ( x ) − H ( x / y ) ] C = \mathop {\max }\limits_{\left\{ {p(x)} \right\}} \left[ {H(x) - H(x/y)} \right] C={p(x)}max​[H(x)−H(x/y)]
另一种是用单位时间（秒）内能够传输的平均信息量最大值表示信道容量C。
C = max ⁡ R { p ( x ) } = max ⁡ { p ( x ) } r [ H ( x ) − H ( x / y ) ] C = \mathop {\max R}\limits_{\left\{ {p(x)} \right\}} = \mathop {\max }\limits_{\left\{ {p(x)} \right\}} r\left[ {H(x) - H(x/y)} \right] C={p(x)}maxR​={p(x)}max​r[H(x)−H(x/y)]

4.2 连续信道容量

连续信道容量也有两种不同的计量单位，只介绍按单位时间计算的容量。
假设输入信道的加性高斯白噪声功率为N(瓦W)，信道的带宽为B(Hz)，信号功率为S(瓦W)，则可以证明，该信道的信道容量为：
$$C_t=B{\log }_2(1+\frac{S}{N})$$
设噪声单边功率谱密度为$n_0$则$N=n_{0}B$,故上式可改写为：
$$C_t=B{\log }_2(1+\frac{S}{n_{0}B})$$