Sutherland–Hodgman 算法介绍(简单易懂)

Curz酥

已于 2023-01-01 18:03:26 修改

阅读量8.7k

点赞数 19

分类专栏：计算机图形学文章标签： c++ 算法图形渲染图像处理

于 2023-01-01 17:35:35 首次发布

本文链接：https://blog.csdn.net/m0_56494923/article/details/128512626

版权

计算机图形学专栏收录该内容

12 篇文章

订阅专栏

文章介绍了Sutherland-Hodgman算法，一种用于裁剪凸多边形的算法，详细描述了算法步骤和计算细节，包括判断点在裁剪线的哪一侧以及求线段交点的方法。该算法不适用于凹多边形，对于凹多边形的裁剪会存在多余线条，推荐使用Weiler-Atherton算法解决这一问题。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

一、算法介绍

我们使用Sutherland–Hodgman算法来裁剪多边形的边，一般是给你一个多边形顶点序列(P1,P2,P3,P4,…Pn)让你裁剪，最终裁剪掉裁剪多边形的外部部分(下图黑框就是裁剪多边形)。像这样：

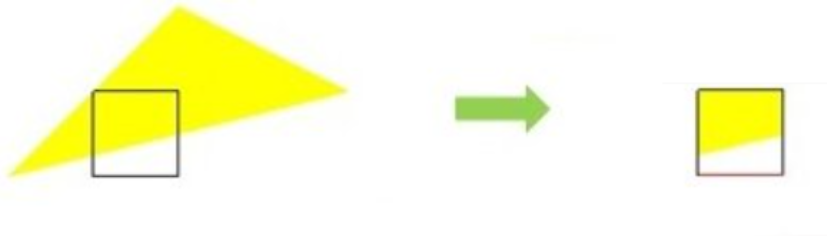
二、算法描述

首先，我们需要了解多边形的各条边与裁剪线的位置关系，一共只有四种：

① 仅输出顶点Pk

② 输出为空

③ 输出交点和Pk

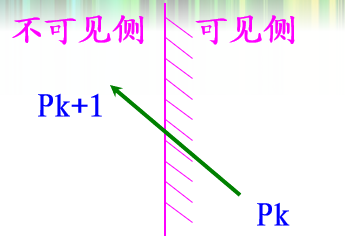
④ 仅输出交点

每次裁剪完，输出一个顶点序列，作为下一次裁剪的输入。于是我们便可以按照如下顺序，对多边形进行裁剪：

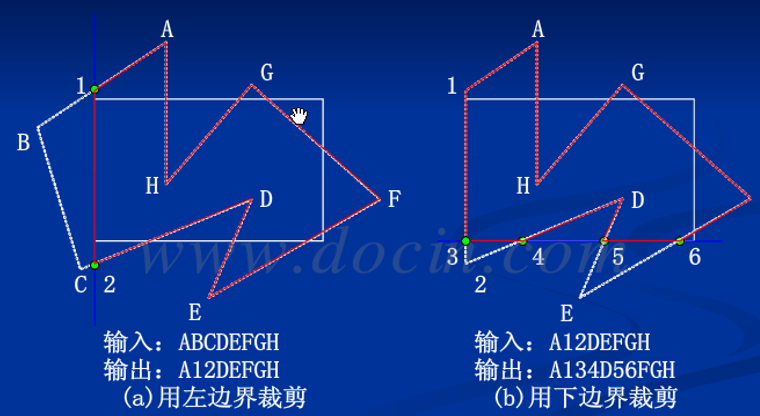
综上，即可完成对多边形的裁剪。

三、计算细节补充

1、如何判断一个点，在裁剪多边形其中一条线的内部还是外部(可见侧还是不可见侧)

解：设你要拿来判断的裁剪多边形的其中一条线段，它的两个端点坐标分别是(x1,y1)，(x2,y2)，你要拿来判断的点的坐标为(x,y)，则可以通过下列公式判断：

如果 P < 0，则这个点位于线的右边

如果 P = 0，则这个点位于线上

如果 P > 0，则这个点位于线的左边

这个公式的使用前提是，题目给你提供的裁剪多边形的顶点序列是顺时针的，这样的话右边就是内部(可见侧)，左边就是外部(不可见侧)。

2、如何求得线段与裁剪多边形其中一条线段的交点

解：设线段两个端点为(x1,y1)，(x2,y2)，裁剪多边形其中一点线段两端点为(x3,y3)，(x4,y4)，则可以通过以下公式求解：

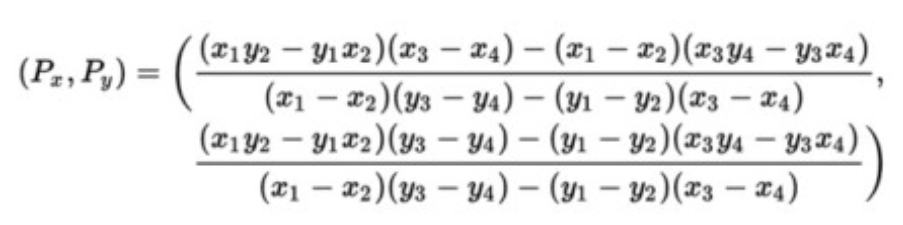
四、算法总结

代码如下，来源(Polygon Clipping | Sutherland–Hodgman Algorithm - GeeksforGeeks)

// C++ program for implementing Sutherland–Hodgman
// algorithm for polygon clipping
#include<iostream>
using namespace std;

const int MAX_POINTS = 20;

// Returns x-value of point of intersection of two
// lines
int x_intersect(int x1, int y1, int x2, int y2,
				int x3, int y3, int x4, int y4)
{
	int num = (x1*y2 - y1*x2) * (x3-x4) -
			(x1-x2) * (x3*y4 - y3*x4);
	int den = (x1-x2) * (y3-y4) - (y1-y2) * (x3-x4);
	return num/den;
}

// Returns y-value of point of intersection of
// two lines
int y_intersect(int x1, int y1, int x2, int y2,
				int x3, int y3, int x4, int y4)
{
	int num = (x1*y2 - y1*x2) * (y3-y4) -
			(y1-y2) * (x3*y4 - y3*x4);
	int den = (x1-x2) * (y3-y4) - (y1-y2) * (x3-x4);
	return num/den;
}

// This functions clips all the edges w.r.t one clip
// edge of clipping area
void clip(int poly_points[][2], int &poly_size,
		int x1, int y1, int x2, int y2)
{
	int new_points[MAX_POINTS][2], new_poly_size = 0;

	// (ix,iy),(kx,ky) are the co-ordinate values of
	// the points
	for (int i = 0; i < poly_size; i++)
	{
		// i and k form a line in polygon
		int k = (i+1) % poly_size;
		int ix = poly_points[i][0], iy = poly_points[i][1];
		int kx = poly_points[k][0], ky = poly_points[k][1];

		// Calculating position of first point
		// w.r.t. clipper line
		int i_pos = (x2-x1) * (iy-y1) - (y2-y1) * (ix-x1);

		// Calculating position of second point
		// w.r.t. clipper line
		int k_pos = (x2-x1) * (ky-y1) - (y2-y1) * (kx-x1);

		// Case 1 : When both points are inside
		if (i_pos < 0 && k_pos < 0)
		{
			//Only second point is added
			new_points[new_poly_size][0] = kx;
			new_points[new_poly_size][1] = ky;
			new_poly_size++;
		}

		// Case 2: When only first point is outside
		else if (i_pos >= 0 && k_pos < 0)
		{
			// Point of intersection with edge
			// and the second point is added
			new_points[new_poly_size][0] = x_intersect(x1,
							y1, x2, y2, ix, iy, kx, ky);
			new_points[new_poly_size][1] = y_intersect(x1,
							y1, x2, y2, ix, iy, kx, ky);
			new_poly_size++;

			new_points[new_poly_size][0] = kx;
			new_points[new_poly_size][1] = ky;
			new_poly_size++;
		}

		// Case 3: When only second point is outside
		else if (i_pos < 0 && k_pos >= 0)
		{
			//Only point of intersection with edge is added
			new_points[new_poly_size][0] = x_intersect(x1,
							y1, x2, y2, ix, iy, kx, ky);
			new_points[new_poly_size][1] = y_intersect(x1,
							y1, x2, y2, ix, iy, kx, ky);
			new_poly_size++;
		}

		// Case 4: When both points are outside
		else
		{
			//No points are added
		}
	}

	// Copying new points into original array
	// and changing the no. of vertices
	poly_size = new_poly_size;
	for (int i = 0; i < poly_size; i++)
	{
		poly_points[i][0] = new_points[i][0];
		poly_points[i][1] = new_points[i][1];
	}
}

// Implements Sutherland–Hodgman algorithm
void suthHodgClip(int poly_points[][2], int poly_size,
				int clipper_points[][2], int clipper_size)
{
	//i and k are two consecutive indexes
	for (int i=0; i<clipper_size; i++)
	{
		int k = (i+1) % clipper_size;

		// We pass the current array of vertices, it's size
		// and the end points of the selected clipper line
		clip(poly_points, poly_size, clipper_points[i][0],
			clipper_points[i][1], clipper_points[k][0],
			clipper_points[k][1]);
	}

	// Printing vertices of clipped polygon
	for (int i=0; i < poly_size; i++)
		cout << '(' << poly_points[i][0] <<
				", " << poly_points[i][1] << ") ";
}

//Driver code
int main()
{
	// Defining polygon vertices in clockwise order
	int poly_size = 3;
	int poly_points[20][2] = {{100,150}, {200,250},
							{300,200}};

	// Defining clipper polygon vertices in clockwise order
	// 1st Example with square clipper
	int clipper_size = 4;
	int clipper_points[][2] = {{150,150}, {150,200},
							{200,200}, {200,150} };

	// 2nd Example with triangle clipper
	/*int clipper_size = 3;
	int clipper_points[][2] = {{100,300}, {300,300},
								{200,100}};*/

	//Calling the clipping function
	suthHodgClip(poly_points, poly_size, clipper_points,
				clipper_size);

	return 0;
}

Sutherland–Hodgman算法的缺点：仅适用于凸多边形，对于凹多边形的裁剪将如图所示显示出一条多余的直线。