BPR:贝叶斯个性化排序推荐

一、问题导入

在很多推荐场景中，我们都是基于现有的用户和商品之间的一些数据，得到用户对所有商品的评分，选择高分的商品推荐给用户，这是矩阵分解之类算法的做法，使用起来也很有效。但是在有些推荐场景中，我们是为了在千万级别的商品中推荐个位数的商品给用户，此时，我们更关心的是用户来说，哪些极少数商品在用户心中有更高的优先级，也就是排序更靠前。也就是说，我们需要一个排序算法，这个算法可以把每个用户对应的所有商品按喜好排序。BPR就是这样的一个我们需要的排序算法。

二、显示反馈与隐式反馈

2.1 显式反馈与隐式反馈基本概念

显式反馈是指:用户明确喜欢和不喜欢的物品。例如：用户对物品的评分，如电影评分。

隐式反馈是指：用户对于浏览过的物品没有明确表示喜欢或厌恶。这种类型数据只能认为全部是正反馈也即喜欢的物品。例如：用户对物品的交互行为，如浏览，购买等，现实中绝大部分数据属于隐式反馈，可以从日志中获取。

2.2 显式反馈与隐式反馈的比较

					表 2-1 显示与隐式反馈的特征

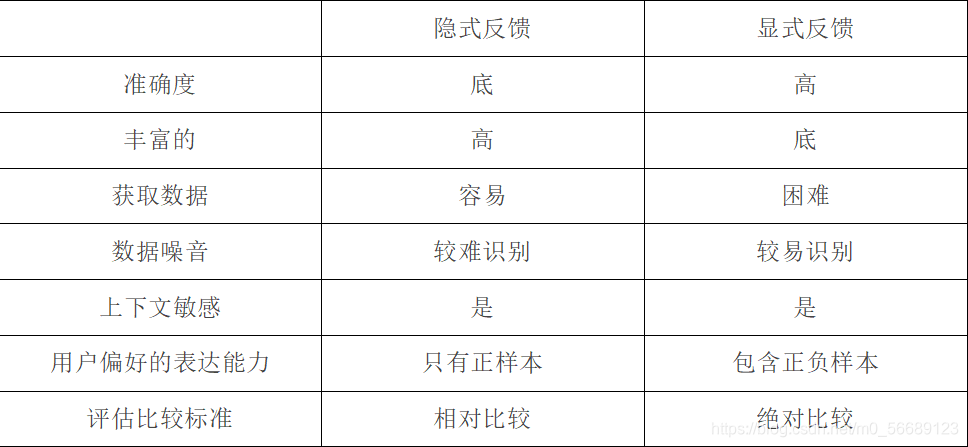
2.3 隐式反馈数据介绍

2.3.1 隐式反馈数据的特点

隐性反馈数据有诸多弊端，例如不明确，具有噪点数据，但是由于他广泛存在，我们有时甚至只能利用它，所以还是要详细研究一下，通过对隐式反馈的合理降噪以及数据修剪来提升物品推荐的可行度。

显性反馈数据可以看出用户对某一物品的偏好值，例如评分机制，8分和10分的区别，而隐性反馈数据没办法衡量偏好值，只能认为用户浏览同一内容越多，越有可能喜好这个内容，也即置信度越大。

2.3.2 隐式反馈数据的处理方式

在使用隐式反馈的情况下，我们会发现观察到的数据均为正例（因为用户对物品交互过才会被观察到），而那些没有被观察到的数据（即用户还没有产生行为的物品），分为两种情况，一种是用户对该物品确实没有星期（负类），另一种是缺失值（即用户以后可能会产生行为的物品），而在传统的个性化推荐中通常是计算用户u对物品i的个性化分数，然后根据个性化分数进行排序。而其处理数据的方式为把所有观察到的隐式反馈作为正类，而其余数据作为负类。

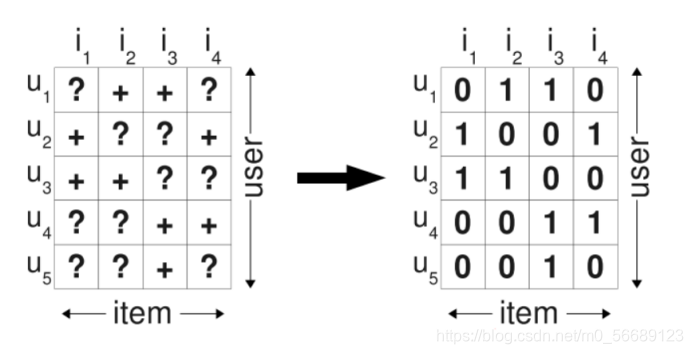
在负类被填零的情况下，我们优化目标变成了希望在预测时观测到的数据预测为1，其余的均为0，于是产生的问题是，我们希望模型在以后预测的缺失值，在训练时却都被认为时负类数据。因此这个模型训练的足够好，那么最总都得到的结果就是这些未观察的样本最后预测值都是0.

而针对与BPR算法是根据隐式反馈数据来进行比较的，通过对问题进行贝叶斯分析得到的最大后验概率来对item进行排序，进而产生推荐。

三、BPR算法概述

3.1 BPR算法基本概念

BPR（Bayesian Personalized Ranking），中文名称为贝叶斯个性化排序，是当下推荐系统中常用的一种推荐算法。与其他的基于用户评分矩阵的方法不同的是BPR主要采用用户的隐式反馈（如点击、收藏、加入购物车等），通过对问题进行贝叶斯分析得到的最大后验概率来对item进行排序，进而产生推荐。

不了解贝叶斯算法的朋友可以先看一下另一篇文章：
https://blog.csdn.net/qq_41529692/article/details/84105315
最开始我没学习贝叶斯时候干撸BPR发掘了这篇文章，通俗易懂

3.2 BPR算法相关定义

既然是基于贝叶斯，那么我们也就有假设，这里的假设有两个：
一是每个用户之间的偏好行为相互独立，即用户u在商品i和j之间的偏好和其他用户无关。
二是同一用户对不同物品的偏序相互独立，也就是用户u在商品i和j之间的偏好和其他的商品无关。
为了便于表述，我们用>u符号表示用户u的偏好，上面的<u,i,j>可以表示为：i>uj。
在BPR中，这个排序关系符号 满足完全性，反对称性和传递性，即对于用户集U和物品集I：
完整性：

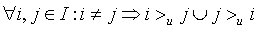
反对称性：

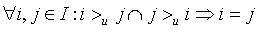
传递性：

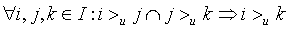
3.3 BPR建模思路

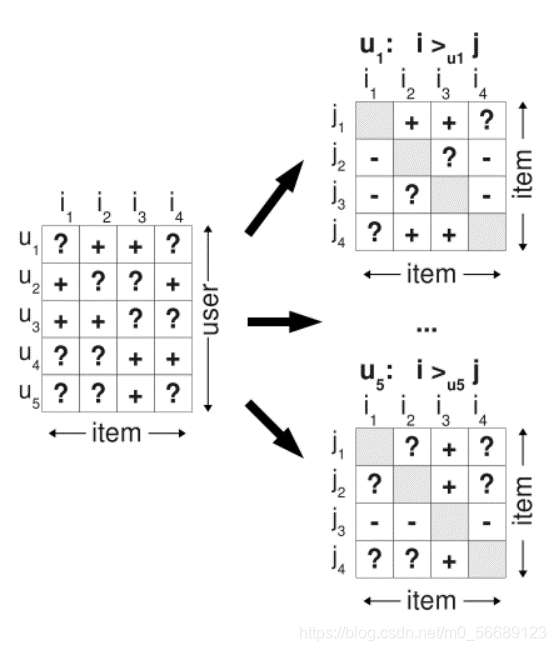
在BPR算法中，我们将任意用户u对应的物品进行标记，如果用户u在同时有物品i和j的时候对i产生了行为，那么我们就得到了一个三元组<u,i,j>，它表示对用户u来说，i的排序要比j靠前。但是如果一个用户对两个物品同时产生过行为，或者同时没有产生行为，则无法构成偏好对。如果对于用户u来说我们有m组这样的反馈，那么我们就可以得到m组用户u对应的训练样本。可以看到BPR采用了pairwise的方式。

那么如下图所示，基于观察到的数据S构建数据集$D_s$，通过对每个用户，可以构建$I\ast I$的偏好矩阵。所有用户的偏好对构成了训练集$D_s=U\ast I\ast I$。

BPR推荐系统会考虑positive value 和negative value,也就说所有item都会被个性化ranking,即使用户对某个item缺失值这个item也能够被ranking，而不是仅仅用negative value代替缺失值。

同时，BPR也用了和funkSVD类似的矩阵分解模型，这里BPR对于用户集U和物品集I的对应的$U\times I$的预测排序矩阵$\overline{X}$，我们期望得到两个分解后的用户矩阵$W(|U|\times k)$和物品矩阵$H(|I|\times k)$，满足$$\overline{X}=W{H}^T$$
这里的k和funkSVD类似，也是自己定义的，一般远远小于$|U|,|I|$。
由于BPR是基于用户维度的，所以对于任意一个用户u，对应的任意一个物品i我们期望有：$${\overline{x}}_{ui}=w_u\ast h_i=\sum _{f=1}^k{w}_{uf}\ast h_{if}$$
最终我们的目标，是希望寻找合适的矩阵$W,H$，让$\overline{X}$和$X$最相似。读到这里，也许你会说，这和funkSVD之类的矩阵分解模型没有什么区别啊？ 的确，现在还看不出，下面我们来看看BPR的算法优化思路，就会慢慢理解和funkSVD有什么不同了。

四、BPR算法优化

BPR 基于最大后验估计$P(W,H|>u)$来求解模型参数$W,H$,这里我们用θ来表示参数$W$和$H$, >u代表用户u对应的所有商品的全序关系,即I-I矩阵,则优化目标是$P(\theta |>u)$。根据贝叶斯公式，我们有：$$P(\theta |>u)=\frac{P(>u|\theta )P(\theta )}{P(>u)}$$
注意我们现在明确了算法思路，下一步就是化简公式的右半部分，让我们能简单地求解。

由于我们求解假设了用户的排序和其他用户无关，那么对于任意一个用户u来说，$P(>u)$对所有的物品一样，所以有：$$P(\theta |>u)\propto P(>u|\theta )P(\theta )$$后验概率正比于似然概率乘上先验概率。

这个优化目标转化为两部分。似然概率$P(>u|\theta )$第一部分和样本数据集D有关，先验概率$P(\theta )$第二部分和样本数据集D无关。

现在我们简化第一部分。
对于第一部分，
独立性假设：
1.每个用户之间的偏好行为相互独立。
2.同一用户对不同物品的偏序相互独立。
所以有：$$\prod _{u\in U}P(>u|\theta )=\prod _{(u,i,j)\in (U\times I\times I)}P(i{>}_{u}j|\theta {)}^{\delta ((u,i,j)\in D)}(1-P(i{>}_{u}j|\theta ){)}^{\delta ((u,j,i)\notin D)}$$其中 δ ( b ) = { 0   e l s e 1   i f   b   i s   t u r e δ(b)=\{^{1\ if\ b\ is\ ture}_{0\ else} δ(b)={0 else1 if b is ture​
上面的式子类似于极大似然估计，若用户u相比于j来说更偏向i，那么我们就希望$P(i{>}_{u}j|\theta )$出现的概率越大越好。

根据上面讲到的完整性和反对称性，优化目标的第一部分可以简化为：$$\prod _{u\in U}P(>u|\theta )=\prod _{(u,i,j)\in D}P(i{>}_{u}j|\theta )$$
而对于$P(i{>}_{u}j|\theta )$这个概率，我们可以使用下面这个式子来代替:$$P(i{>}_{u}j|\theta )=\sigma ({\overline{x}}_{uij}(\theta ))$$
其中，σ(x)是sigmoid函数。$\sigma (x)=\frac{1}{1+e^{-x}}$
σ里面的项我们可以理解为用户u对i和j偏好程度的差异，我们当然希望i和j的差异越大越好，这种差异如何体现，最简单的就是差值：$${\overline{x}}_{uij}(\theta )={\overline{x}}_{ui}(\theta )-{\overline{x}}_{uj}(\theta )$$，${\overline{x}}_{ui}(\theta ),{\overline{x}}_{uj}(\theta )$就是我们的矩阵$\overline{X}$对应位置的值。这里为了方便，我们不写θ,这样上式可以表示为:$${\overline{x}}_{uij}={\overline{x}}_{ui}-{\overline{x}}_{uj}$$
最终，我们的第一部分优化目标转化为：$$\prod _{u\in U}P(>u|\theta )=\prod _{(u,i,j)\in D}\sigma ({\overline{x}}_{ui}-{\overline{x}}_{uj})$$

对于第二部分$P(\theta )$，原作者大胆使用了贝叶斯假设，即这个概率分布符合正太分布，且对应的均值是0，协方差矩阵是$\lambda \theta I$,即$$P(\theta )\sim N(0,\lambda \theta I)$$原作者为什么这么假设呢？个人觉得还是为了优化方便，因为后面我们做优化时，需要计算$lnP(\theta )$，而对于上面假设的这个多维正态分布，其对数和$||\theta |{|}^2$成正比。即：$$lnP(\theta )=\lambda ||\theta |{|}^2$$
下面是式子手写推导

最终对于我们的最大对数后验估计函数$$lnP(\theta |>u)\propto lnP(>u|\theta )P(\theta )=ln\prod _{(u,i,j)\in D}\sigma ({\overline{x}}_{ui}-{\overline{x}}_{uj})+lnP(\theta )=\sum _{(u,i,j)\in D}ln\sigma ({\overline{x}}_{ui}-{\overline{x}}_{uj})+\lambda ||\theta ||2$$这个式子可以用梯度上升法或者牛顿法等方法来优化求解模型参数。如果用梯度上升法，对θ求导，我们有：$$\frac{\partial lnP(\theta |>u)}{\partial \theta }\propto \sum _{(u,i,j)\in D}\frac{1}{1+e^{{\overline{x}}_{ui}-{\overline{x}}_{uj}}}\frac{\partial ({\overline{x}}_{ui}-{\overline{x}}_{uj})}{\partial \theta }+\lambda \theta$$

由于$${\overline{x}}_{ui}-{\overline{x}}_{uj}=\sum _{f=1}^k{w}_{uf}{h}_{if}-\sum _{f=1}^k{w}_{uf}{h}_{jf}$$这样我们可以求出：

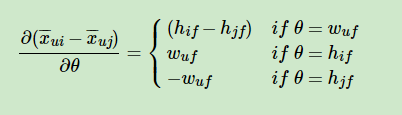
　有了梯度迭代式子，用梯度上升法求解模型参数就容易了。下面我们归纳下BPR的算法流程。

五. BPR算法流程

面简要总结下BPR的算法训练流程：　　
输入：训练集D三元组，梯度步长α， 正则化参数λ,分解矩阵维度k。

输出：模型参数，矩阵$W,H$

1. 随机初始化矩阵W,H
2. 迭代更新模型参数：
   
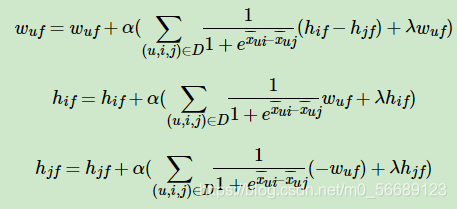
   3.如果$W,H$收敛，则算法结束，输出$W,H$，否则回到步骤2.

当我们拿到$W,H$后，就可以计算出每一个用户u对应的任意一个商品的排序分：${\overline{x}}_{ui}=w_u\bullet h_i$，最终选择排序分最高的若干商品输出。

六.BPR小结

BPR是基于矩阵分解的一种排序算法，但是和funkSVD之类的算法比，它不是做全局的评分优化，而是针对每一个用户自己的商品喜好分贝做排序优化。因此在迭代优化的思路上完全不同。同时对于训练集的要求也是不一样的，funkSVD只需要用户物品对应评分数据二元组做训练集，而BPR则需要用户对商品的喜好排序三元组做训练集。

参考文献

https://www.cnblogs.com/pinard/p/9128682.html
https://www.jianshu.com/p/ba1936ee0b69
原论文：
http://yun.baidu.com/share/link?shareid=2431171172&uk=1009675359