土体本构关系

土体本构关系

应力应变分析

柯西应力

可以表示为以下矩阵形式

$\sigma =\left[\begin{array}{ccc}{\sigma }_{xx}& {\sigma }_{xy}& {\sigma }_{xz}\\ {\sigma }_{yx}& {\sigma }_{yy}& {\sigma }_{yz}\\ {\sigma }_{zx}& {\sigma }_{zy}& {\sigma }_{zz}\end{array}\right]$

在任意方向上的应力可以通过柯西应力张量与该方向的单位法向量 $\vec{n}$ 相乘来求解：

$\vec{n}=\left[\begin{array}{c}{n}_x\\ n_y\\ n_z\end{array}\right]$

$\vec{n}$表示该方向上的单位法向量

向量 $\vec{t}=[t_x,t_y,t_z{]}^T$ 表示在法向量 $\vec{n}$ 指定方向上的应力分量

法向应力：沿法向量 $\vec{n}$ 方向的分量，表示为 ${\sigma }_n=\vec{t}\cdot \vec{n}$ 。

剪应力：垂直于法向应力方向的分量，大小为 $\tau =\sqrt{|\vec{t}{|}^2-{\sigma }_n^2}$ 。

八面体应力

在主应力的空间中有四面体等倾面所以根据上文可知其中 $\vec{n}=\begin{bmatrix} \frac{1}{\sqrt{3}}\ \frac{1}{\sqrt{3}} \ \frac{1}{\sqrt{3}} \end{bmatrix} $ 可以得到 ${\sigma }_8=(\frac{1}{\sqrt{3}}{\sigma }_1,\frac{1}{\sqrt{3}}{\sigma }_2,\frac{1}{\sqrt{3}}{\sigma }_3)$

${\tau }_{oct}=\frac{1}{3}\sqrt{({\sigma }_1-{\sigma }_2{)}^2+({\sigma }_2-{\sigma }_3{)}^2+({\sigma }_3-{\sigma }_1{)}^2}$

${\tau }_{oct}=\sqrt{\frac{2J_2}{3}}$

• 土体材料存在剪胀性，体积变形不仅与应力球张量相关，还会由剪应力产生。

$\pi$平面

基本概念 由三个主应力${\sigma }_1$${\sigma }_2$${\sigma }_3$作为坐标轴构成三维空间，对于某一个点P（${\sigma }_1$${\sigma }_2$${\sigma }_3$）能描述土中一点的应力状态，满足某些特征的面或者线为研究土力学提供了方便，如$\pi$平面

所以把垂直于空间对角线的平面称之为偏平面
这里注意一下$\pi$平面上应力和八面体应力之间的关系在数值上差一个八面体面的方向余弦

注意相应的条件是${\sigma }_1$+${\sigma }_2$+${\sigma }_3$=k其中k为一常数

应力罗德角

（Lode angle）是用来描述应力状态的方向性，尤其是在三轴应力状态下的中间主应力（${\sigma }_2$）的影响。应力罗德角是一个衡量应力状态偏离纯剪切或纯拉压的参数。它通常用于一些屈服准则（如Drucker-Prager准则）中，以描述不同方向上的屈服行为。

$K_0$固结

K₀固结指的是土体在侧向约束条件下的固结状态，即土样在保持水平应力不变的情况下，竖向承受荷载，从而发生竖向变形。此过程通常用于模拟地基土体在自重作用下的自然应力状态。

土体强度准则

土体是松散的颗粒集合体，比起颗粒自身压碎更容易产生滑移破坏，所以土体的强度就是指抗剪强度。基本不能抗拉，所以认为一般不能承受拉应力。

这里思考一下抗剪和抗拉的区别

土是一种摩擦类型材料，抗剪强度与正应力有关系。正应力越大能承受的剪应力越大，这种特性被称为压硬性。

通常土体强度准则的数学描述是$F({\sigma }_{ij},k_f)$​，其中$k_f$表示土体特征参数是一个试验参数

屈瑞斯卡准则

在饱和不排水的条件下，剪切强度与静水压力无关对于$k_f$表示不排水试验中的剪切强度$c_u$

摩尔-库伦准则

在$\pi$平面上绘制出的摩尔库伦强度包线中能很清楚的发现，三轴压缩强度大于三轴伸长强度。

其中当$\theta$为0时表示三轴压缩状态，当其为60度时表示三轴伸长状态。

在$\pi$平面（即主应力空间的横截面）中，摩尔-库仑准则产生了一个六边形破坏包络。这个包络在三轴压缩和三轴伸长的应力路径上不对称，这意味着材料在这两种加载路径上的强度表现不同。具体而言：

在三轴压缩中，由于最大主应力 ${\sigma }_1$较大，材料更容易沿该方向产生剪切破坏，因此表现出较高的抗剪强度。

在三轴伸长中，最小主应力 ${\sigma }_3$较小，容易在拉应力作用下发生破坏，因此抗剪强度相对较低。

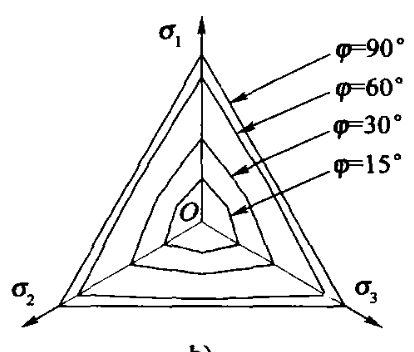
上图显示了随着摩擦角增大，$\pi$平面的强度不断增大，当摩擦角增大到90度是在 $\pi$平面的摩尔库伦强度包线为正三角形。