直方图均衡化(HE)和限制对比度自适应直方图均衡化(CLAHE)学习和理解

星云一桶

于 2025-03-08 19:22:47 发布

阅读量902

点赞数 8

文章标签：学习

本文链接：https://blog.csdn.net/m0_58581666/article/details/146117930

版权

1、直方图均衡化（HE）

英文：Histogram Equalization
原因：灰度直方图不够舒展，集中在了一个小区域.
方法：找到一个函数映射，使直方图均衡，能在显示范围内均衡显示。而累加直方图正好满足这个映射条件。
在这里插入图片描述

原图及其直方图、累加直方图：

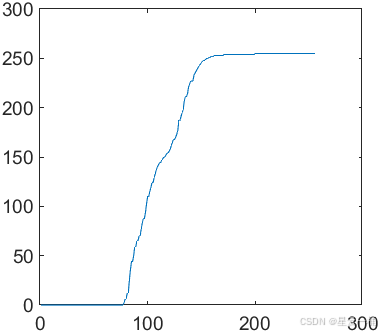
在这里插入图片描述
直方图均衡化后的图像及其直方图、累加直方图

在这里插入图片描述

2、限制对比度自适应直方图均衡化(CLAHE)

英文：Contrast Limited Adaptive Histogram Equalization
原因:
如果一个图片中有大块的暗区或者亮区的话，普通直方图算法(HE)效果非常不好。
1、对于灰度非常集中的区域，直方图会被拉的非常稀疏，从而导致对比度增强过大，成为噪音；
2、整体直方图后,一些小色块区域被压缩合并到一块，调整后丢失细节。
下面是一个例子，发现经过HE之后的图片出现了大量噪点：
在这里插入图片描述
方法:
1、针对第一个问题，提出了CLHE，加入对比度限制，其实原理很简单，设置直方图分布的阈值，将超过该阈值的分布“均匀”分散至概率密度分布上，由此来限制转换函数（累计直方图）的增幅。

2、对于第二个问题，自适应直方图均衡化(Adaptive HE)的基本思想是将原始图片划分成子区域，然后对每个子区域进行直方图变换。当然，这样做的问题应该是显而易见的：每一块区域之间都会有非常大的不连续。如下:
在这里插入图片描述
因此为了解决这个问题，提出了优化方案双线性插值的AHE，

PS:
双线性插值是一种用于二维空间的插值方法，它通过对四个相邻像素点的加权平均来计算目标点的值，从而实现平滑的过渡。
在这里插入图片描述

3、综合以上两点，分块+截断，就变成了我们现在的CLAHE算法。
这样的话，直方图就不会出现概率密度函数过大的区域，从而避免了某些集中区域被拉得过于系数，也能保留一些小色块细节。
在这里插入图片描述

我这里配合 GPT简单写了代码，但这个代码没有考虑边缘和角落的情况，但用来理解原理是没什么问题的。

function output = myCLAHE_optimized(img, tileSize, clipLimit, numBins)
    % 转换为灰度图像并转为单精度
    if size(img, 3) == 3
        img = rgb2gray(img);
    end
    img = single(img); % 使用单精度节省内存
    [imgHeight, imgWidth] = size(img);
    
    % 计算分块数量（不扩展图像）
    numTilesX = ceil(imgWidth / tileSize(2));
    numTilesY = ceil(imgHeight / tileSize(1));
    
    % 预分配三维矩阵存储映射表
    maps = zeros(numTilesY, numTilesX, numBins, 'single');
    
    % 处理每个tile的直方图
    for i = 1:numTilesY
        for j = 1:numTilesX
            % 计算 tile 边界
            xStart = max(1, (j-1)*tileSize(2) + 1);
            xEnd = min(imgWidth, j*tileSize(2));
            yStart = max(1, (i-1)*tileSize(1) + 1);
            yEnd = min(imgHeight, i*tileSize(1));
            tile = img(yStart:yEnd, xStart:xEnd);
            
            % 计算直方图并应用 CLAHE
            h = imhist(uint8(tile), numBins); % imhist 需要 uint8 输入
            avg = numel(tile) / numBins;
            clipVal = avg * clipLimit;
            
            % 直方图裁剪
            excess = sum(max(h - clipVal, 0));
            hClipped = min(h, clipVal) + excess / numBins;
            
            % 计算 CDF 并生成映射
            cdf = cumsum(hClipped);
            if cdf(end) == 0
                map = single(0:numBins-1)';
            else
                map = single(round((cdf / cdf(end)) * (numBins - 1)));
            end
            maps(i,j,:) = map;
        end
    end
    
    % 预计算 x 和 y 方向的 tile 索引及插值权重
    xCoords = (1:imgWidth);
    yCoords = (1:imgHeight);
    
    tx = (xCoords - 1) / tileSize(2);
    ty = (yCoords - 1) / tileSize(1);
    
    x1 = floor(tx);
    y1 = floor(ty);
    x1 = max(0, min(numTilesX-1, x1));
    y1 = max(0, min(numTilesY-1, y1));
    x2 = min(x1 + 1, numTilesX-1);
    y2 = min(y1 + 1, numTilesY-1);
    
    dx = tx - x1;
    dy = ty - y1;
    
    % 转换为1-based索引
    x1 = uint32(x1 + 1); 
    y1 = uint32(y1 + 1);
    x2 = uint32(x2 + 1);
    y2 = uint32(y2 + 1);
    
    % 将灰度值映射到 bin 索引（1~numBins）
    binIdx = uint8(floor(img / 255 * (numBins-1)) + 1); % uint8 索引
    
    % 预分配输出
    output = single(zeros(imgHeight, imgWidth));
    
    % 遍历图像并应用插值
    for i = 1:imgHeight
        yi1 = y1(i);
        yi2 = y2(i);
        dy1 = 1 - dy(i);
        dy2 = dy(i);
        
        for j = 1:imgWidth
            xi1 = x1(j);
            xi2 = x2(j);
            dx1 = 1 - dx(j);
            dx2 = dx(j);
            
            % 提取四个相邻 tile 的映射值
            map11 = maps(yi1, xi1, binIdx(i,j));
            map12 = maps(yi1, xi2, binIdx(i,j));
            map21 = maps(yi2, xi1, binIdx(i,j));
            map22 = maps(yi2, xi2, binIdx(i,j));
            
            % 插值计算
            output(i,j) = dy1 * (dx1 * map11 + dx2 * map12) + ...
                          dy2 * (dx1 * map21 + dx2 * map22);
        end
    end
    
    % 转换为 uint8 输出
    output = uint8(output);
end

% 读取图像
img = imread('pout.tif');

% 设置参数
tileSize = [60 60];   % Tile尺寸
clipLimit =200;   % 对比度限制参数
numBins = 256;      % 直方图bin数量

% 应用CLAHE
enhancedImg = myCLAHE_optimized(img, tileSize, clipLimit, numBins);

% 显示结果
imshowpair(img, enhancedImg, 'montage');
title('原图 (左) vs CLAHE增强后 (右)');