P3768 简单的数学题杜教筛*

Strezia

已于 2022-07-07 23:56:29 修改

阅读量186

点赞数 1

分类专栏：数学文章标签：算法

于 2022-07-07 22:53:14 首次发布

本文链接：https://blog.csdn.net/m0_59273843/article/details/125667004

版权

数学专栏收录该内容

37 篇文章

订阅专栏

P3768
杜教筛+狄利克雷卷积

题意

给出 $p,(n\leq10^{10})$ ，求 $(\sum_{i=1}^n\sum_{j=1}^nijgcd(i,j)) \mod p$

思路

利用重要卷积 $\phi*1$ 替换 $g c d (i, j)$ 。
$\sum_{i=1}^n\sum_{j=1}^nijgcd(i,j) = \sum_{i=1}^n\sum_{j=1}^nij\sum_{d|i,d|j}\phi(d)=\sum_{d=1}^n \phi(d)d^2\sum_{i=1}^\frac ndi\sum_{j=1}^{\frac nd}j$ $=\sum_{d=1}^n\phi(d)d^2(\sum_{i=1}^{\frac nd}i)^2$

上式后半部分可以 $O (1)$ 求，考虑用杜教筛优化前半部分。
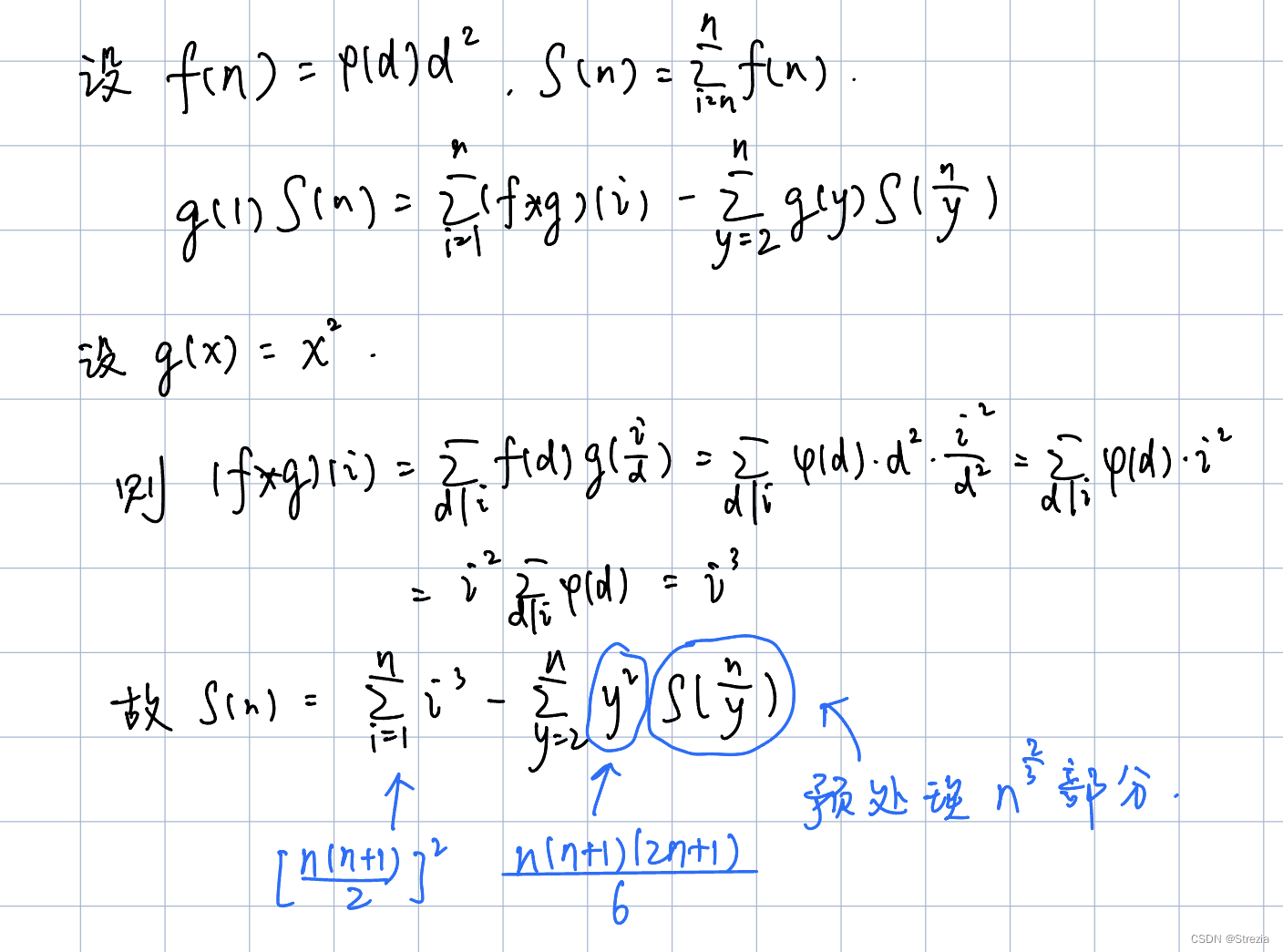
在这里插入图片描述
$S(n)=\sum_{d=1}^n\phi(d)d^2=(\frac {n(n+1)}2)^2-\sum_{y=2}^ny^2S(\frac ny)$

附莫反做法
在这里插入图片描述

代码

int n, P;
ll power(ll a, ll b) {
    ll ans = 1;
    a = a % P;
    for(; b; b >>= 1) {
        if(b & 1) ans = ans * a % P;
        a = a * a % P;
    }
    return ans;
}
bool isnp[maxn];//maxn大小为n^(2/3)
vector<int> primes;
ll phi[maxn], sphi[maxn];//分别记录欧拉函数值及前缀和
map<ll, ll> umsphi;//存大于n^(2/3)的值
void init(int n) // 筛欧拉函数 n为n^(2/3)
{
    phi[1] = 1;
    for (int i = 2; i <= n; i++)
    {
        if (!isnp[i])
            primes.push_back(i), phi[i] = i - 1;
        for (int p : primes)
        {
            if (p * i > n)
                break;
            isnp[p * i] = 1;
            if (i % p == 0)
            {
                phi[p * i] = phi[i] * p;
                break;
            }
            else
                phi[p * i] = phi[p] * phi[i];
        }
    }
    for(int i = 1; i <= n; ++i)
        sphi[i] = (sphi[i - 1] + i * i % P * phi[i] % P) % P;
}
int inv2, inv6;
int s2(int x) {
    x %= P;
    return x * (x+1) % P * (2 * x + 1) % P * inv6 % P;
}
int s3(int x){
    x%=P;
    return (x*(x+1)/2)%P*((x*(x+1)/2)%P)%P;
}
int s4(int x){
    x%=P;
    return (x*(x+1)/2)%P;
}
ll sum_phi(ll n)
{
    if (n < maxn)
        return sphi[n];
    if (umsphi.count(n))
        return umsphi[n];
    ll ans = s3(n);
    for (ll l = 2, r; l <= n; l = r + 1)
    {
        r = n / (n / l);
        ans = (ans - (s2(r)-s2(l-1)+P)%P * sum_phi(n / l) % P + P) % P;
    }
    umsphi[n] = ans;
    return ans;
}
void solve() {
    cin >> P >> n;
    inv2 = power(2, P - 2);
    inv6 = power(6, P - 2);
    init(5e6);
    int ans = 0;
    for(int l = 1, r; l <= n; l = r + 1) {
        r = n / (n / l);
        ans = (ans + (sum_phi(r)-sum_phi(l-1)+P)%P * s3(n/l) % P) % P;
    }
    cout << ans << endl;
}