【最优传输论文十五】Normalized Wasserstein for Mixture Distributions with Applications in Adversarial Learning

羊驼不驼a

已于 2023-07-19 22:30:40 修改

阅读量127

点赞数

分类专栏：最优传输文章标签：人工智能深度学习

于 2023-07-19 11:42:34 首次发布

本文链接：https://blog.csdn.net/m0_60231311/article/details/131737796

版权

对于混合分布，建立的距离度量，如Wasserstein距离，没有考虑不平衡的混合比例。因此，即使两个混合分布具有相同的混合成分，但混合比例不同，它们之间的Wasserstein距离也会很大。这通常会导致基于远程的混合分布学习方法产生不期望的结果。在本文中，通过引入归一化Wasserstein度量来解决这个问题。关键思想是引入混合比例作为优化变量，有效地规范化Wasserstein公式中的混合比例。与普通的Wasserstein距离相比，使用所提出的归一化Wasserstein度量可以显著提高混合比例不平

摘要由CSDN通过智能技术生成

论文：2019 ICCV - Normalized Wasserstein for Mixture Distributions with Applications in
Adversarial Learning and Domain Adaptation

1.motivation

对于混合分布，建立的距离度量，如Wasserstein距离，没有考虑不平衡的混合比例。因此，即使两个混合分布具有相同的混合成分，但混合比例不同，它们之间的Wasserstein距离也会很大。这通常会导致基于远程的混合分布学习方法产生不期望的结果。

在本文中，通过引入归一化Wasserstein度量来解决这个问题。关键思想是引入混合比例作为优化变量，有效地规范化Wasserstein公式中的混合比例。与普通的Wasserstein距离相比，使用所提出的归一化Wasserstein度量可以显著提高混合比例不平衡的混合分布的性能。作者在几个基准数据集上证明了该方法在gan、领域自适应和对抗聚类中的有效性。

2.introduce

混合分布是随机变量 X 的概率分布，其中 X = Xi，概率为πi ，其中1 ≤ i ≤ k。K为混合成分的数量， $\pi =\left [ \pi _{1},...,\pi _{k} \right ]^{T}$ 是混合(或模式)比例的向量。每个Xi的概率分布被称为一种混合成分（或模式）。混合分布自然出现在数据包含两个或多个子种群的不同应用程序中。例如，具有不同标签的图像数据集可以被视为混合(或多模式)分布，其中具有相同标签的样本表示一个特定的混合成分。

如果两个混合分布具有完全相同的混合成分（即相同的Xi）和不同的混合比例（即不同的π），则两者之间的经典距离度量将很大。这可能会在几种基于距离的机器学习方法中导致不期望的结果。

两个分布PX和PY之间的Wasserstein距离，定义为

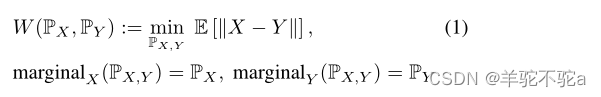
其中 $\mathbb{P}_{X,Y}$ 是其边际分布等于 $\mathbb{P}_{X}$ 和 $\mathbb{P}_{Y}$ 的联合分布（或耦合）。当没有混淆的时候，为了简化表示法，在一些方程中，本文使用W（X，Y）表示法而不是W（PX，PY）。

Wasserstein距离优化适用于所有联合分布（耦合） $\mathbb{P}_{X,Y}$ 。当 $\mathbb{P}_{X}$ 和 $\mathbb{P}_{Y}$ 是具有不同混合物比例的混合物分布时，非常不同的混合物组分的样品必须在 $\mathbb{P}_{X,Y}$ 中耦合在一起（例如图1（a）），使用这种距离度量可能会导致诸如领域适应之类的问题的不期望的结果。

在本文中提出了一种新的距离测度，该测度解决了多模式分布中混合比例不平衡的问题。本文主要对Wasserstein距离方程（1）进行优化。然而，本文的想法也可以自然地扩展到其他距离度量（例如对抗性距离）。

设G是具有k个分量的生成函数的数组，定义为G:=[G1，…，Gk]。设 $\mathbb{P}_{G,\pi }$ 是随机变量X的混合概率分布，其中 $X=G_{i}(Z)$ ，概率为πi，其中1≤i≤k。在本文中，假设Z具有正态分布。

通过放松经典Wasserstein距离（1）的边缘约束，本文引入归一化Wasserstein测度（NW测度）如下：

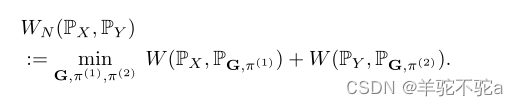
这个定义中有两个关键思想，有助于解决混合分布的模式不平衡问题。

首先，没有直接测量 $\mathbb{P}_{X}$ 和 $\mathbb{P}_{Y}$ 之间的Wasserstein距离，而是构建了两个中间（潜在的混合）分布，即 $\mathbb{P}_{G,\pi^{(1)}}$ 和 $\mathbb{P}_{G,\pi^{(2)}}$ 。这两种分布具有相同的混合物成分（即相同的G），但可以具有不同的混合物比例（即 $\pi ^{(1)}$ 和 $\pi ^{(2)}$ 可以不同）。其次，混合比例 $\pi ^{(1)}$ 和 $\pi ^{(2)}$ 被认为是优化变量。这在Wasserstein距离计算之前有效地规范了混合物比例。参见图1（b，c）中的示例，了解 $\mathbb{P}_{G,\pi^{(1)}}$ 和 $\mathbb{P}_{G,\pi^{(2)}}$ 的可视化以及重新归一化步骤。

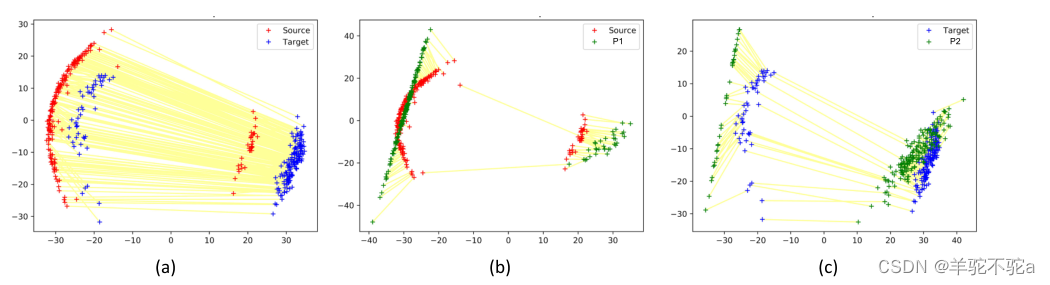
图1。源域（红色）和目标域（蓝色）具有两种模式比例不同的模式。（a）通过估计源和目标分布之间的Wasserstein距离（如黄线所示）计算的耦合与来自不同类和遥远模式分量的几个样本相匹配。（b，c）本文提出的归一化Wasserstein测度（3）构建了中间混合物分布P1和P2（以绿色显示），其混合物成分分别与源分布和目标分布相似，但具有优化的混合物比例。与基线相比，这显著减少了来自错误模式的样本之间的耦合数量，并导致域自适应中的目标损失减少42%。

2. Normalized Wasserstein Measure

G是定义为G:=[G1，…，Gk]的生成函数的数组，其中Gi:Rr→Rd 设G是所有可能的G函数数组的集合。设π是一个具有k个元素的离散概率质量函数，即π=[π1，π2，··，πk]，其中 $\pi _{i}\geq 0$ ， $\sum _{i}\pi _{i}=1$ 。设 $\Pi$ 是所有可能π的集合。

设 $\mathbb{P}_{G,\pi }$ 是混合分布，即它是随机变量X的概率分布，使得 $X=G_{i}(Z)$ ，概率πi为1≤i≤k。假设Z具有正态密度，即Z～N（0，i）。将G和π分别称为混合物组分和比例。

所有这些混合物分布的集合定义为：

其中k是混合物组分的数量。给定属于混合分布 $P_{G,k}$ 族的两个分布 $\mathbb{P}_{X}$ 和 $\mathbb{P}_{Y}$ ，本文感兴趣的是定义一个距离测度，该距离测度与模式比例的差异无关，但对模式分量的变化敏感，即，只有当PX和PY的模式分量不同时，距离函数才应具有高值。如果PX和PY具有相同的模式分量，但仅在模式比例上不同，则距离应该较低。

主要思想是在Wasserstein距离公式（1）中引入混合比例作为优化变量。称之为归一化Wasserstein测度（NW测度）， $W_{N}(\mathbb{P}_{X},\mathbb{P}_{Y})$ ，定义为：

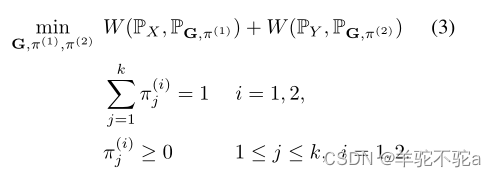
由于归一化的Wasserstein优化（3）包括混合比例 $\pi ^{(1)}$ 和 $\pi ^{(2)}$ 作为优化变量，如果两个混合分布具有相似的混合成分，但混合比例不同，尽管两者之间的Wasserstein距离可能很大，但引入的两者之间的归一化Wasserstein测度将为零。注意，WN是关于一组生成函数G=[G1，…，Gk]定义的。NW测度是半距离测度（而不是距离)。

为了计算NW测度，本文使用了一种交替梯度下降方法，类似于Wasserstein距离的对偶计算。此外，使用softmax函数来施加π约束。

通过估计两个分布之间的Wasserstein距离产生的耦合如图1-a中的黄线所示。来自不相同混合物成分的样品之间存在许多耦合。另一方面，归一化Wasserstein测度构建了中间模式归一化分布P1和P2，它们分别耦合到源分布和目标分布的正确模式（见图1中的（b）和（c））。

3. Theoretical Results

为了使NW测量有效地工作，必须适当地选择NW公式（等式（3））中的模式数k。例如，给定两个分别具有k个分量的混合分布，具有2k个模式的归一化Wasserstein测度将始终给出0值。首先对希望计算其NW距离的两个混合分布X和Y进行以下假设：

（A1）如果分布X中的模i和分布Y中的模j属于同一混合物组分，则它们的Wasserstein距离≤ $\epsilon$ 即，如果Xi和Yj对应于相同的成分，则 $W(\mathbb{P}_{X_{i}},\mathbb{P}_{Y_{j}})< \epsilon$ 。

（A2）一种混合物分布的任何两种模式之间的最小Wasserstein距离至少为δ，即 $W(\mathbb{P}_{X_{i}},\mathbb{P}_{X_{j}})>\delta$ 和

最低0.47元/天解锁文章

羊驼不驼a

关注

0
点赞
踩
0

收藏

觉得还不错? 一键收藏
0
评论
【最优传输论文十五】Normalized Wasserstein for Mixture Distributions with Applications in Adversarial Learning

对于混合分布，建立的距离度量，如Wasserstein距离，没有考虑不平衡的混合比例。因此，即使两个混合分布具有相同的混合成分，但混合比例不同，它们之间的Wasserstein距离也会很大。这通常会导致基于远程的混合分布学习方法产生不期望的结果。在本文中，通过引入归一化Wasserstein度量来解决这个问题。关键思想是引入混合比例作为优化变量，有效地规范化Wasserstein公式中的混合比例。与普通的Wasserstein距离相比，使用所提出的归一化Wasserstein度量可以显著提高混合比例不平
复制链接

扫一扫