图匹配的定义与形式化
什么是图匹配?
图匹配就是将两个图中的各个节点一一对应起来,不仅要求匹配的节点相似度高,而且要求节点之间的连线,也就是边的相似度也要高。

图匹配问题可以分成两个类别:
①精确图匹配(Exact Graph Matching):要求每个节点和对应的边都准确的与另一个图匹配对应,且相似度达到最高。该约束严格,求解难度大,而且在实际应用中也很少存在这种情况。
②非精确图匹配(Inexact Graph Matching):将图匹配问题转化为寻找能够使节点相似度和边相似度之和最大化的一个优化问题;其允许两个图有差别,甚至允许一定程度的错误匹配,但要求能让节点和边的相似度尽可能的大。
图的描述方式
将图定义为一个四元组
:表示节点的特征,
表示特征维度,
表示节点个数
:表示边的特征,
表示特征维度,
表示节点个数
:描述了节点和边的对应关系,也就是这个图的结构;
表示边的起点,
表示边的终点,如下图表示


表示边的起点,
表示边的终点,如图(b)中G1中点1为“1”,H1中点2为“1”,则代表一条边从1指向2,图中所有的边都如此表示
图匹配的定义
给定两个图和
并定义两个关联矩阵
:表示两幅图节点和节点之间的相似度
如左图中的节点2和右图中的节点a相似,在下图中对应2行a列数值为“10”

:表示两幅图边和边之间的相似度
如图,行代表左图的边,列代表右图的边,比较两个边的相似度

:表示图
中的第
个节点和图
的第
个节点之间的相似程度
:表示图
中的第
个边和图
的第
个边之间的相似程度
图匹配问题就变成寻找两幅图之间最优的匹配关系,使节点间相似度和边之间相似度之和最大

式(1)中第一项表示匹配节点之间的相似度之和

式(1)中第二项表示匹配边之间的相似度之和

其中表示了两幅图节点之间的匹配关系,
表示图
中的第
个节点和图
的第
个节点匹配
节点之间的匹配关系要满足一一对应的约束,即为一个置换矩阵:

其中表示长度为
且元素均为1的列向量
允许图和图
的尺寸不相同(即节点数目不相同),为不失一般性,我们约定
;式(2)约束图
中的每个点都与
中的点有唯一对应的匹配关系。
图匹配的两种形式化方式
为了更加清晰地描述和表达图匹配的目标,将节点和边的关联矩阵统一为一个关联矩阵,如下图所示


中的对角线元素表示了节点之间的相似度,也就是原来的
;

非对角线元素表示边之间的相似度,也就是,例如非对角线元素
就表示了图
中
和
节点之间的边与图
中
和
节点之间的边的相似程度。

有了关联矩阵就很容易的将图匹配问题形式化为一个二次分配问题(QAP)
式(3)即为被广泛采用的Lawler’s QAP范式:
![]()
除此之外还有另一种形式化方式,Koopmans-Beckmann’s QAP:

式(4)中的第一项表示节点之间的相似度,第二项表示边之间的线性相似度。
加权邻接矩阵,
分别表示图
与图
各个节点间的软连接关系
注意:加权邻接矩阵的元素是从之间的权重值,表示两个节点之间的连接强度
第二项是线性相似度:只能通过边的权重值之间的内积大小来描述边和边的相似性,而Lawler’s QAP中的
可以采用包括高斯核函数在内的非线性相似性度量方式。
当时,Lawler’s QAP退化为Koopmans-Beckmann’s QAP

图匹配的松弛与求解算法
尽管非精确图匹配相对于精确图匹配已经做了一定的松弛,但其仍然是一个NP-hard问题。
因此需要继续对置换矩阵约束(公式(2))进行松弛,以近似求解图匹配问题。

常用的松弛策略包含以下几种:
①谱松弛(Spectral Relaxation):
(1)Umeyama等人将置换矩阵松弛为正交矩阵,即
,则图匹配问题可以通过计算特征值的方式求得闭式解,但这类方法只能用于Koopmans-Beckmann’s QAP形式的图匹配问题。(2)Leordeanu等人将
松弛为单位长度,即
,则最优的匹配关系
即为
的主特征向量。但这种松弛方式,忽略一对一对应的约束条件,并且只计算主特征向量是对
做了秩为1的近似,但实际上
通常是满秩的。因此该方法计算的准确性较差。
②半正定规划松弛(Semidefinite-programming (SDP) Relaxation):
半正定规划(SDP)是一类标准的凸优化问题。
通过引入一个新的变量,将图匹配问题的非凸约束松弛为
的半正定凸约束。
利用SDP算法求解,然后再采用随机算法或赢家通吃策略近似求解得到
这类方法的优势在于理论上能够保证在多项式时间内找到近似解。然而在实际应用中,由于的尺寸是
尺寸的平方,使得求解SDP问题的成本十分高昂。
③双随机松弛(Doubly-stochastic Relaxation):
将松弛为一个双随机矩阵(矩阵的每行之和与每列之和均为1),
,其为置换矩阵的一个凸包
![]()
和
的区别:
的取值范围从
变为了
,这一改变使得图匹配问题松弛为非凸的二次规划问题(Quadratic Programming,QP),有许多方法可以找到局部最优解。
(1)Zaslavskiy等人采用路径跟随算法来求解该非凸的二次规划问题
(2)Gold and Rangarajan提出毕业分配算法利用泰勒展开式将目标函数分解为一系列线性近似,再通过迭代的方式求解
因式分解的图匹配:
图匹配问题的定义和现有方法存在的问题:
关联矩阵是图匹配问题中的关键,它编码了两幅图之间的一阶和二阶关系。
的两个特性:满秩性(Full-rankness)和不定性(Indefinitenes)给许多传统方法(如谱方法和基于梯度的方法)带来了困难。

上图中的第一行分别展示了三个数据集中矩阵的秩
和行数
之间的比值,可以看到比值全为1;说明
通常是满秩的,这使得将
近似为秩为1的矩阵的谱方法不可避免地失去准确性。
第二行展示了的最大特征值
和最小特征值
之间的比值,可以看到比值均小于-0.4,即特征值异号,说明
是不定矩阵;这说明最大化
的过程是非凸(像山地一样有很多起伏)的,使得基于梯度的方法容易陷入局部最优。
FGM:
关联矩阵是由对角线元素(节点关联矩阵
)和非对角线元素(边关联矩阵
)构成的,如上图所示。
除掉对角线元素,是一个稀疏的块矩阵且具备以下三个结构特点:

①由
个更小的块
构成

②有些块是零矩阵,这说明图
中第
个和第
个节点之间没有边连接,这些零矩阵可以通过
来检索,即如果
,则对应的块
③对于非零的块有封闭形式的解
,其中
是图
第
个和第
个节点之间的下标
基于上述结构特点,关联矩阵可以被分解为:

利用上式大矩阵被分解为6个小矩阵的组合,使算法复杂度下降
将公式(6)带入公式(3)中可得等价的图匹配目标函数公式(7)
![]()
![]()
其中

图匹配的统一框架:
FGM基于因式分解的方法提出一种统一的图匹配框架。
边关联矩阵可以通过SVD方法分解为
,利用
本身的低秩结构特点
![]()
公式(7)可以重写为:

,
:两个图对应的邻接矩阵
而公式(7)原本是由公式(3)(Lawler’s QAP)推导而来
![]()
经过上面的转化却可以写成类似Koopmans-Beckmann’s QAP的形式
当时,公式(9)就退化为公式(4)也就是Koopmans-Beckmann’s QAP

当时,求解Lawler’s QAP可以看作是
个Koopmans-Beckmann’s QAP的组合优化问题
路径跟随算法(Path-Following Algorithm)求解FGM
定义:图匹配的优化过程中,沿着某条优化路径前进,以逐步逼近最优解。
传统的求解图匹配问题通常分成两个步骤:
①将GM进行连续性松弛,求解松弛后的问题得到一个近似的解
②将近似解取整得到一个二元解
但这类方法有两个限制:
①虽然经过了连续性松弛,但由于问题是非凸的因此容易陷入局部最优
②圆整的步骤不可避免地会导致精度损失。
圆整:在优化和数学计算中通常指的是将连续变量的解转换为离散解
为了解决上述问题,作者提出一种基于路径跟随算法地迭代优化策略,这一策略有三个理论优势:
①优化的效果与初始化条件无关
②最终解确保可以收敛到一个整数解,因此无需额外的圆整步骤
③迭代更新的步骤可以利用一些数值型连续求解方法的思想,这些方法已经广泛用于求解
凸松弛和凹松弛
定义:
匹配矩阵本来是一个排列矩阵,但离散优化问题难解,把
的取值范围扩展到实数域,就能用连续优化方法求解。
凸松弛:用一个凸优化问题来近似原始的匹配问题,使优化更容易
凹松弛:用一个凹优化问题来逼近匹配问题,让解更接近整数匹配
方法:
为了应用路径跟随算法,我们首先要找到的一个凸松弛和凹松弛,为了实现这个要求,我们引入了一个辅助函数:

由于置换矩阵也是一个正交矩阵,因此
,所以
是一个常数

将代入到
中可以构造得到两个等价的目标函数:

对于包含任意置换矩阵和正交矩阵的,优化过程中上述两个函数都将达到相同的结果,且差值为一个常数
;由于
和
的Hessian矩阵(二阶导数矩阵)分别为:

是半负定和半正定的,因此最大化和
分别是凸优化和凹优化问题。
路径跟随策略
作者通过迭代优化如下一系列的凸-凹问题来求解非凸的图匹配问题

:用于平衡凸松弛和凹松弛之间的平衡系数,在迭代过程中从0逐步增长到1
路径跟随策略的优势体现在三个方面:
①,该问题是一个纯粹的凸优化问题,数值型的优化器可得到与初始化无关的全局最优解
②(迭代的终点),该问题是一个凹优化问题,局部的最优点通常在约束集合的极值点上。根据Birkhoff-von Neumann定理,所有的形成Birkhoff多面体的双随机矩阵,其顶点都是置换矩阵。也就是说局部最优点会收敛为置换矩阵,也就保证收敛的解为二元解,而无需进行圆整操作
③平滑的从0增长到1过程,与基于梯度方法相比,路径跟随算法更有可能找到更好的局部最优解

如图所示, 和
时,
分别为
和
;当
从0到1的增长过程中,
是单调递减而
单调递增的,表明
部分对于
的影响不断增强;当
时,
和
曲线相交;当
时,
与
和
两个松弛项之间的差值为一个常数
子问题优化
采用的是Frank-Wolfe’s algorithm (FW)算法解决在特定的下优化求解
首先给定一个初始的,FW算法不断更新
,直至收敛。
在每次迭代过程中,需要计算两个内容:优化的方向和优化步长
。通过求解一下线性规划问题来计算
:

上述目标函数是在
处的一阶近似,
可以采用矩阵操作计算:

上述线性规划问题(公式(17))可采用Hungarian算法求解。

得到梯度后,最优的是下述抛物线的最大值点:
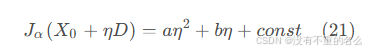
根据抛物线的特点,最大值点可能为
点配准
点配准与图匹配
与图匹配问题类似,点配准问题是指给定两组点集和
,点配准的目标就是寻找两个点集中点和点之间的对应匹配关系,并获得两个点集之间的几何变换关系。该目标是通过最小化两个点集中点和点之间的距离之和来实现的:

: 表示点和点之间的对应关系;在点配准问题中,点和点之间可以是一对一,也可以是多对一,本文只关注一对一的情况。
:是一个用参数
描述的几何变换
:是一个用于约束变换参数
的惩罚函数
与图匹配对比:
共同点:优化目标需要寻找点和点之间的对应关系
不同点:点配准中两组点之间存在某种特定的几何变换关系,图匹配中没有这种约束条件;但图匹配除了关注点和点之间的匹配关系,还会关注边和边之间的匹配关系
点配准联系图匹配:
定义节点关联矩阵,其中的每一个元素为
,表示节点之间欧氏距离的负值,则原目标函数(公式(21))可以改写为
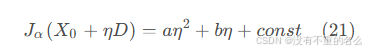

给定变换参数,最小化上述目标函数就等价于最大化公式(7)中的节点相似度,这个优化问题可以看作是线性匹配问题。
![]()
如果是一对一的匹配,可用匈牙利算法求解,如果
是多对一的匹配,可采用赢家通吃策略求解。通常
和
都是未知的,需要进行联合优化,该问题是一个非凸问题,无法求得闭式解。通常采用迭代的交替最小化算法进行求解,如EM算法。简单来说,就是固定
,优化
;然后再固定
,优化
,交替进行直至两者都收敛。
几何变换
①相似变换(Similarity Transformation)
给定一个点或一个点集
,相似变换的计算过程为:
或
:表示放缩系数
:表示旋转矩阵
:平移向量
对旋转矩阵有一个约束条件
必须是单位正交阵,即
②仿射变换(Affine Transformation)
给定一个点或一个点集
,仿射变换的计算过程为:
或
:表示仿射矩阵
:表示平移向量
③RBF非刚性变换(RBF Non-rigid Transformation)
RBF非刚性变换的参数化取决于基点的选择,本文选择第二个点集中的点作为基点。
给定一个点或一个点集
,RBF非刚性变换计算点与其初始位置之间的位移:
或
:表示权重矩阵
:表示与基点相对应的
个位移函数
:表示点
和基点
之间的位移函数
:表示带宽
:定义在所有成对基点上的RBF核函数
变换关系如下表所示

可变形的图匹配
图匹配是一种广泛应用于具备相似结构点集匹配的工具。但在很多计算机视觉任务中,匹配的两个点集之间需要满足一定的几何约束。目前尚不清楚如何将几何约束统一到图匹配的方法中。本文介绍了一种可变形图匹配(Deformable Graph Matching, DGM)方法能够将刚性和非刚性变换引入到图匹配中。
目标函数:
将图定义为一个四元组,为了简化问题并且尽量与点配准问题保持一致,此处选择节点的坐标作为节点特征
,选择边所连接的两个节点的坐标差值
作为边的特征
。在这种情况下,边的特征可以用矩阵形式计算
给定两个图和
,两组点之间的几何变换为
,计算节点关联矩阵
和边关联矩阵

选择一个较大的数以保证边的相似性为非负值。与点配准问题相似,为了让图匹配对于几何变换更加鲁棒,DGM不仅要找到最优的对应关系
还要找到最优的变换参数
,则优化的目标函数为:

用于平衡节点和边的重要性,当
时,上述目标函数等价为点配准问题,
但
已知时,上述目标由等价为图匹配问题。
优化策略
由于目标函数的非凸属性,本文采用与点配准相似的优化策略,交替优化和
。对DGM问题而言,初始化非常重要,但如何选择一个好的初始化参数已经超过本文的范畴。本文简单地将变换参数初始化为同等变换,即
。给定
时,上述优化问题变成图匹配问题,可以采用前文介绍的路径跟随算法求解最优的
。给定
时,可参考点配准方法求解最优的
。针对上文所述的几种常见几何变换,均可求得闭式解。
相似变换
![]()
根据公式(25),边特征的相似变换为或
,由于平移变换
只会影响节点特征,不会影响边的特征,因此当最优旋转矩阵
和最优放缩系数
已知时,最优平移向量
可得:
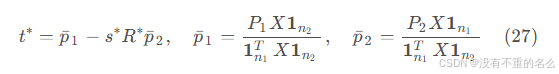
经过数据中心化操作,最优旋转矩阵
和最优放缩系数
为:

其中
仿射变换
与相似变换接近,边特征的仿射变换为或
,最优平移向量为:

最优的仿射变换为
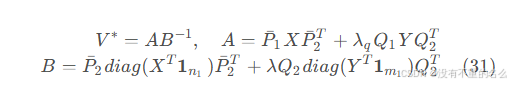
RBF非刚性变换
边特征的非刚性变换为或
,
,最优的权重矩阵

实验:
图(a)中展示了三种不同程度的相似变换(由蓝色到红色)

图(b)中展示了ICP算法在迭代24次时,在不同程度的变换作用下,目标函数值得情况。目标函数值越接近于0,表示匹配效果越好,可以看到在旋转角度为时,ICP算法陷入了局部最优,无法得到最优得匹配结果。

图(c)中展示了DGM算法在不同迭代次数下,不同程度得变换作用下,目标函数值得情况。可以看到虽然在迭代初期,在大部分得变换条件下,匹配效果不尽人意。但随着迭代次数增加,匹配效果越来越好,当迭代24次时,在所有得变换条件下均能达到最优匹配。


























 2940
2940

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








