
1.1.1 网络流的基本概念
基本概念
问题 → \to → 建图转化为网络流的模型 → \to → 建图得到的最优解和原问题是否等价.
流网络
网络流是对于一个有向图来说的.
流网络是一个有向图(可以有环).
图是由一些点和有向边组成的,流网络中有两个特殊的点,一个叫源点 s s s,一个叫汇点 t t t.
流网络中的每一条边都有一个属性,叫做流网络的容量 c c c.
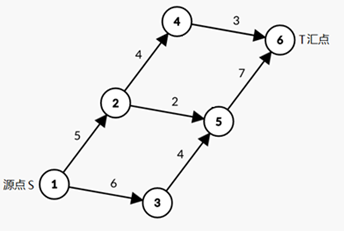
图 1中的源点 S S S 应为源点 s s s,汇点 T T T 应为 汇点 t t t.
流网络可以比作一个河流问题:
- 每个点都是河流的交汇点,每条边都是一条河;
- 每条边的容量就代表这条河每秒流过的水的量是多少(或者河的宽度、深度之类).
流网络还可以想象成水管中运输水的模型:
- 每条边可以想象成一条水管,容量为水管每秒最多流过的的单位水量.
源点有源源不断、无穷多的流量流出,可以想象为一个无穷大的水库.
汇点可以想象为大海,可以容纳无穷多的流量.
整个模型可以看作:
- 源点让水,通过管道,源源不断地流向汇点的过程.
流网络可以记作 G = ( V , E ) G=(V,E) G=(V,E),即点集和边集.
为了简化问题,假定流网络中一定不存在反向边.
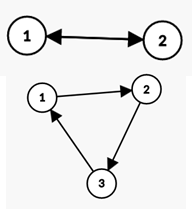
图 2如图 2,因为对于有反向边的图,可以在中间添加一个点,等价地变成没有反向边.
如果一条边不存在,则定义其容量 c ( u , v ) = 0 c(u,v)=0 c(u,v)=0.
可行流
对于每一个流网络而言,考虑它任意一个可行流.
可行流一般用 f f f 来表示,指指定每一条边的流量,或者每个水管每秒的水流速率,就是每条边自行给它设定一个值,只要满足两个条件,它就是一个可行的流:
- 满足容量限制:每条边流过的流量不能超过它的容量,记为:
0 ≤ f ( u , v ) ≤ c ( u , v ) . 0 \leq f(u,v) \leq c(u,v). 0≤f(u,v)≤c(u,v). - 满足流量守恒:对于整个网络来说,除了源点 s s s 与汇点 t t t 外,其余所有点不存储流量,记作:
∀ x ∈ V / ( s , t ) ∑ ( V , x ) ∈ E f ( V , x ) = ∑ ( x , V ) ∈ E f ( x , V ) . \forall x \in V/(s,t)\quad \sum_{(V,x)\in E}f(V,x)=\sum_{(x,V)\in E}f(x,V). ∀x∈V/(s,t)(V,x)∈E∑f(V,x)=(x,V)∈E∑f(x,V).
注意,上述描述不考虑反向边,因为有些文章说需要满足 3. f ( x , y ) = − f ( y , x ) f(x,y)=-f(y,x) f(x,y)=−f(y,x),但是流量怎么会是负的呢?所以考虑反向边的话,定义不是很自洽.
可行流 f f f 表示的是一种方案.
可行流的流量值
每秒从源点流到汇点的流量的具体值(速率、流量值),将其定义为 可行流的流量值 ∣ f ∣ |f| ∣f∣,换言之,可以将可行流的流量值定义为:
- 每秒从源点流出去的流量;
- 每秒流入汇点的流量.
一般用源点来定义,即每秒从源点流向其他点的总流量 减去 每秒从其他点流入源点的总流量,记为
∣ f ∣ = ∑ ( s , V ) ∈ E f ( s , V ) − ∑ ( V , s ) ∈ E f ( V , s ) . |f|=\sum_{(s,V)\in E}f(s,V)-\sum_{(V,s) \in E}f(V,s). ∣f∣=(s,V)∈E∑f(s,V)−(V,s)∈E∑f(V,s).
一般网络是不会往源点流入的,但可能有些特殊网络是会有这种情况的,为了更具一般性,在定义中都写上.
对于一个流网络来说,会有很多个可行流,每一个可行流都可以求一个流量值,一般说的最大流,指的是流量值最大的可行流,故其可以称为最大可行流.
视全部可行流的流量值为一个集合,求最大流 就可以类比为 在集合中求最大值.

图 3中的源点 S S S 应为源点 s s s,汇点 T T T 应为 汇点 t t t.
如图 3,红色字体为一种可行流,且显然为一种最大可行流,其可行流的流量值为 3 + 6 = 9 3+6=9 3+6=9.
流量是 0 0 0 的话,可以定义成可行流,也可以忽略它.
残留网络
残留网络是对于流网络的某一条可行流来说的,可行流不同的话,残留网络也不同.
残留网络(残存网络、残量网络)记为 G f G_f Gf ,与可行流一一对应 { f 1 → G f 1 , f 2 → G f 2 . \begin{cases}f_1 \to G_{f_1}, \\ f_2 \to G_{f_2}. \end{cases} { f1→Gf1,f2→Gf2.
残留网络是如何定义的呢?
-
G f G_f Gf 的点集和原图的点集是一样的,记作 V f = V V_f=V Vf=V;
-
G f G_f Gf 的边集不仅包含原图的所有边,同时包含 E E E 中的所有反向边,记作 E f = E + E 反 E_f=E+E_反 Ef=E+E反;
-
残留网络实际上也是一个流网络,其每条边的容量有两种情况:
-
对于原图中存在的边(正向边), c ′ ( u , v ) c'(u,v) c′(u,v) 定义为可以增加的流量,记作 c ( u , v ) − f ( u , v ) ( u , v ) ∈ E c(u,v)-f(u,v) \quad (u,v) \in E c(u,v)−f(u,v)(u,v)∈E;
-
对于原图的反向边, c ′ ( u , v ) c'(u,v) c′(u,v) 定义为可以退回去多少,相当于后悔,记作 f ( v , u ) ( v , u ) ∈ E f(v,u) \quad (v,u) \in E f(v,u)(v,u)∈E.
-
为什么会有退回去的情况?例子如下图 4( 1 1 1 号点为源点 s s s, 4 4 4 号点为汇点 t t t)所示:
如果用 容量为 1 1 1 的这条边的话,流量值并不是最大的,所以应该有退回去的操作.
这也能间接解释残留网络为什么要建反向边.

图 4
- 对于任意一个流网络 G G G 的可行流 f f f,都可以求出来一个残留网络 G f G_f Gf,如下右图为左图的残留网络(红色边为反向边,黑色边为正向边):

残留网络也是一个流网络,所以残留网络也是由可行流的概念,记残留网络 G f G_f Gf 的可行流为 f ′ f' f′,讨论 原网络的可行流 f f f 与其的关系.
定理: f + f ′ f+f' f+f








 最低0.47元/天 解锁文章
最低0.47元/天 解锁文章














 4410
4410











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








