
阅读须知:
探索者安全团队技术文章仅供参考,未经授权请勿利用文章中的技术资料对任何计算机系统进行入侵操作,由于传播、利用本公众号所提供的技术和信息而造成的任何直接或者间接的后果及损失,均由使用者本人负责,作者不为此承担任何责任,如有侵权烦请告知,我们会立即删除并致歉,创作不易转载请标明出处.感谢!
我是 Breeze ,今天我给大家分享一个关于RSA的题目,带大家领略 密码学 的魅力。
今天开始前,我们先学习一下 费马定理 。
费马定理
若 p为素数,则对任意a有
ap = 1 (mod p)
可以变形为 ap = a (mod p)
[GKCTF 2021]RRRRsa
赛题复现https://www.nssctf.cn/problem/1393
整理整理我们知道的信息
求解p
首先对于 hint1,我们对其进行二项式展开。在这里我给大家具体讲讲为什么展开是这个样子。
对于hint2,我们对其使用 费马小定理,因为它的指数是q1。我们将其改写
我们来对比一下 hint1和hint2
我们给第一个式子乘以 2021202020, 第二个式子幂方202020次。再乘以2021202020。
#根据c1 = pow(p,e1,n1)
q1=n1//p1
d=Crypto.Util.number.inverse(e1,(p1-1)*(q1-









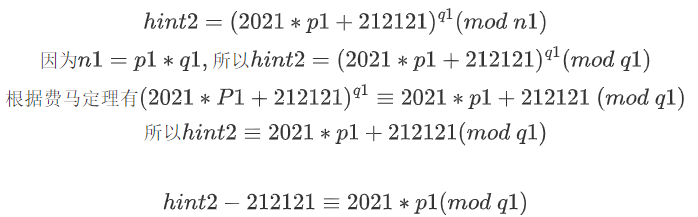
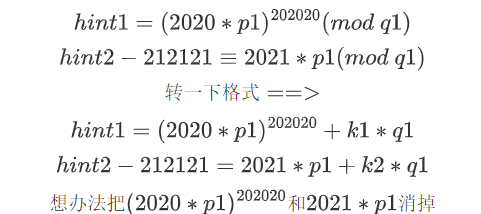
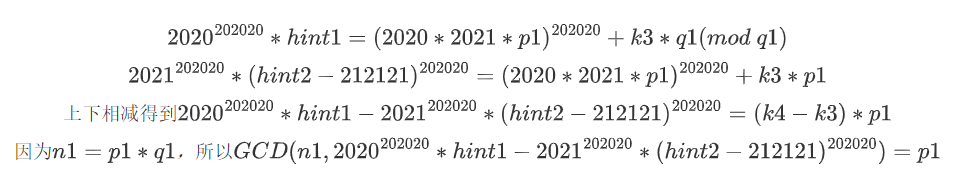
 最低0.47元/天 解锁文章
最低0.47元/天 解锁文章















 1455
1455

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








