常系数线性齐次递推关系得求解
常系数线性齐次递推关系的定义
{f(n)}为一个数列,形如
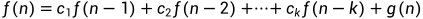
k为正整数,g(n)不为0,f(n)就为k阶线性非齐次递推关系,
若g(n)为0,f(n)就为k阶线性齐次递推关系,
若c都为常数,f(n)就为k阶常系数线性递推关系。
特征方程与特征根的定义
方程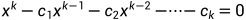 为f(n)的特征方程,它的解q1,q2,...,qn为f(n)的特征根。
为f(n)的特征方程,它的解q1,q2,...,qn为f(n)的特征根。
引理一
若q为特征方程的特征根,则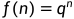 是递推关系的解。
是递推关系的解。
证明:
若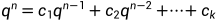 ,又因为q不等于0,则
,又因为q不等于0,则 。
。
反之亦然。
引理二
若h1(n)和h2(n)都是f(n)的解,b1,b2是常数,则b1h1(n)+b2h2(n)也是f(n)的解。
证明:
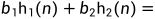
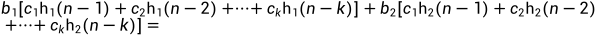
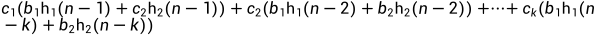
所以b1h1(n)+b2h2(n)也是f(n)的解。
所以f(n)可以表示为
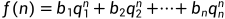
通解的定义
f(n)的每一个解都可以有一组常数d1,d2,...,dk表示为
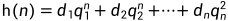
则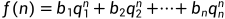 为f(n)的通解。
为f(n)的通解。
也就是说递推关系具有初始值,每一个解的常系数都是唯一的,那么我们就要证明b1,b2,...,bn是唯一的,令f(0)=b1+b2+...+bn=a0,f(1)=b1q1+b2q2+...+bnqn,...,那么就有方程组
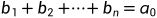
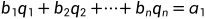
...

方程组的系数行列式为范德蒙德行列式,如图

每个q都不相同,所以行列式不为0,则解唯一,也就是通解中的常系数唯一。
重根的情况
假设特征根出现二重根q,则对应的解就是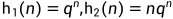 。
。
若是k重根,则对应的解就是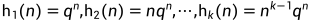 。
。
证明:
首先证明二重根,若q是特征方程的二重跟,则 等式变换得
等式变换得 。对两边边求导,得到的等式具有一个根q
。对两边边求导,得到的等式具有一个根q 。再对等式两边乘以q,得到的等式具有一个根q
。再对等式两边乘以q,得到的等式具有一个根q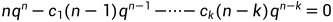 发现nq^n满足递推关系,二重根的解即证。多重根则对等式多次求导再乘以q,同样能证明。
发现nq^n满足递推关系,二重根的解即证。多重根则对等式多次求导再乘以q,同样能证明。
常系数线性非齐次递推关系的求解
常系数线性非齐次递推关系的形式为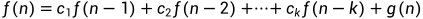 。
。
解的形式
常系数齐次递推关系的通解加上常系数非齐次递推关系的特解。f(n)=f1(n)+f2(n),其中f1(n)为f(n)=c1f(n-1)+c2f(n-2)+...+ckf(n-k)的通解,f2(n)为f(n)=c1f(n-1)+c2f(n-2)+...+ckf(n-k)+g(n)的特解。
一般的g(n)的特解
g(n) | 特征方程P(x) | 特解形式 |
|
|
|
|
| |
|
|
|
1为P(X)=0的m重根 |
| |
|
|
|
|
|









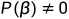

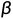 为P(X)=0的m重根
为P(X)=0的m重根
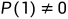
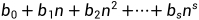

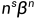
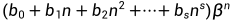
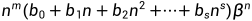














 2443
2443











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








