拉姆齐问题
命题一
任意6个人,其中总有3个人认识或者三个人不认识。
这个问题就等价于 完全图,对它的边进行红蓝两个颜色任意着色,其中一定存在一个红色
完全图,对它的边进行红蓝两个颜色任意着色,其中一定存在一个红色 或者蓝色
或者蓝色 (同色三角形)。
(同色三角形)。
证明:
一个顶点与每个其它5个顶点连线,根据鸽巢原理,至少有 条边同色,不妨设3条边为红色,2条边为蓝色
条边同色,不妨设3条边为红色,2条边为蓝色

假如v2v3,v3v4,v2v4任意一条边为红色,则出现红色 ,假如全部为蓝色边,则出现蓝色
,假如全部为蓝色边,则出现蓝色 ,即证。
,即证。
命题二
对完全图 进行红蓝两色任意着色,都至少有两个同色三角形(意思为每个三角形的每条边同色,不同三角形不一定同色)。
进行红蓝两色任意着色,都至少有两个同色三角形(意思为每个三角形的每条边同色,不同三角形不一定同色)。
证明:根据例一已经得出一定有一个同色三角形,不妨令v1v5v6为蓝色三角形,然后进行分类讨论。
(1)假设v1v2,v1v3,v1v4全是红边,则v2v3,v3v4,v2v4任意一条边为红色,就会又出现一个同色三角形,假设都是蓝色,则v2v3v4为蓝色 ,即出现一个同色三角形。
,即出现一个同色三角形。

(2)假设v1v2,v1v3,v1v4其中有一条为蓝色边,不妨设v1v4为蓝色
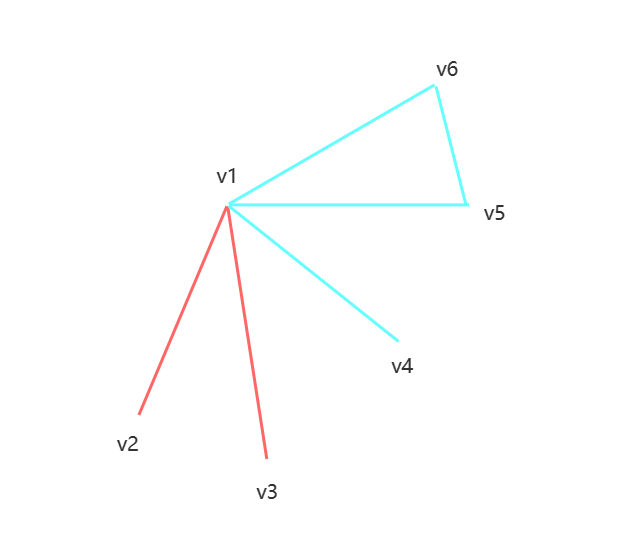
就会出现以下两种情况:
(i)v4v5,v4v6任意一条为蓝色,就会出现一个蓝色三角形

(ii)v4v5,v4v6均为红边

又分两种情况
第一种情况v4v2,v4v3只要有一条边为红边,则回到了例一的情况

这里一定出现一个同色三角形
第二种情况v4v2,v4v3全为蓝边,也可以回到例一的情况

也一定出现一个同色三角形
所以综上, 完全图一定有两个同色三角形。
完全图一定有两个同色三角形。
命题三
 一定有一个红色
一定有一个红色 (蓝色
(蓝色 )或者蓝色
)或者蓝色 (红色
(红色 )
)
证明:
一个顶点a关联的边数为9条,根据鸽巢原理可知,要么至少6条红边,要么至少4条蓝边。

(1)以a为顶点红色边大于等于6条,不妨先画出6条红色边
首先与a关联的6条红边另一头所关联的6个顶点所构成的 (即上面一张图的bcdefg)有一个蓝色
(即上面一张图的bcdefg)有一个蓝色 ,如图bcd
,如图bcd

即证。
否则,根据命题一,与a关联的6条红边的另一头所关联的6个顶点所构成的 一定有一个红色
一定有一个红色 ,然后这个
,然后这个 和顶点a以及a的连线构成红色
和顶点a以及a的连线构成红色 ,如图abcd
,如图abcd

即证。
(2)
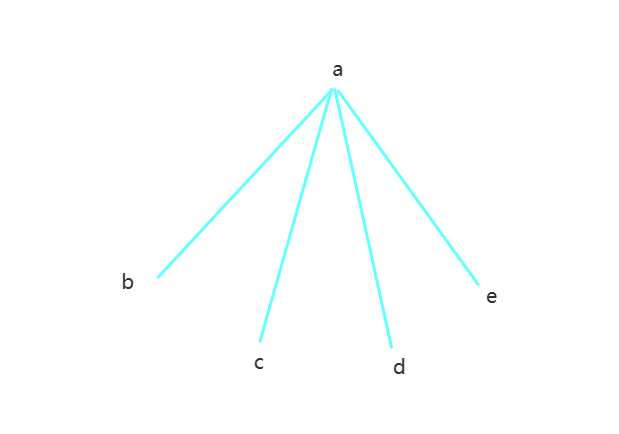
以a为顶点的蓝色边大于等于4,不妨画出4条蓝边
首先假设与a关联的4条蓝边另一头所关联的4个顶点构成的 (即上面一张图的bcde)其中至少有一条蓝边(只要有一条蓝边),则这条蓝边以及它的顶点和a以及a的连线构成蓝色
(即上面一张图的bcde)其中至少有一条蓝边(只要有一条蓝边),则这条蓝边以及它的顶点和a以及a的连线构成蓝色 (如图abc)
(如图abc)

否则这个 为红色
为红色 (如图bcde)
(如图bcde)

命题四
 一定有一个红色
一定有一个红色 或者蓝色
或者蓝色 。
。
证明:假设每个顶点关联的边都有5条红边,则红边总数不为整数,那么总有一个顶点要么至少6条红边要么至少4条蓝边,我们又回到了命题三的证明,所以得证。
拉姆齐数
对于任意给定的整数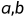 ,存在最小整数
,存在最小整数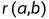 ,使得任意
,使得任意 ,
, 任意进行红蓝两色着色,都存在红色
任意进行红蓝两色着色,都存在红色 或者蓝色
或者蓝色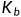 。
。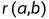 为拉姆齐数。
为拉姆齐数。
可以通过找到刚刚不满足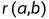 的要求数
的要求数 ,来证明
,来证明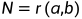 。
。
例如证明 。
。
我们已知 ,我们只需证明
,我们只需证明 有不满足的情况。如图
有不满足的情况。如图
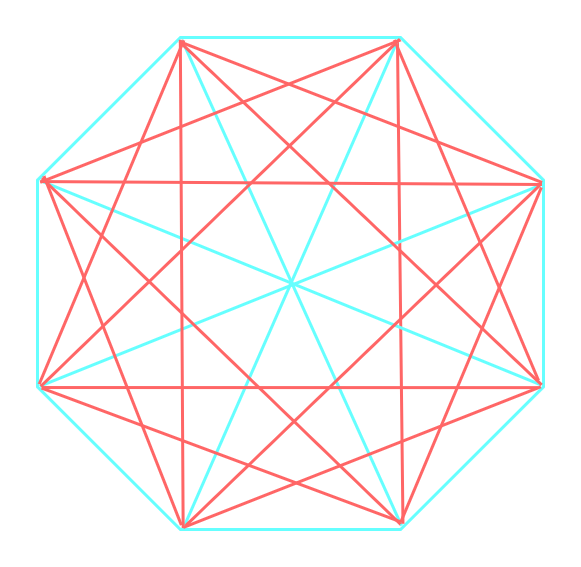
所以 。
。
易证:
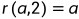
定理:对任意正整数 ,有
,有

若 和
和 都是偶数,则严格成立。
都是偶数,则严格成立。
证明:令 ,
, 中的一个顶点a所关联的边数为
中的一个顶点a所关联的边数为 ,根据鸽巢原理,
,根据鸽巢原理, 中要么至少存在
中要么至少存在 条红边,要么至少存在
条红边,要么至少存在 条蓝边。
条蓝边。
(1)假如至少存在 条红边,那么与a关联的
条红边,那么与a关联的 条红边另一头所关联的顶点构成的
条红边另一头所关联的顶点构成的 ,要么出现红色
,要么出现红色 ,与顶点a以及
,与顶点a以及 条红边构成
条红边构成 ,要么出现蓝色
,要么出现蓝色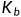 ,所以
,所以 。
。
(2)假设至少存在 条蓝边,那么与a关联的
条蓝边,那么与a关联的 条蓝边另一头所关联的顶点构成的
条蓝边另一头所关联的顶点构成的 ,要么出现红色
,要么出现红色 ,要么出现蓝色
,要么出现蓝色 ,与顶点a以及
,与顶点a以及 条蓝边构成
条蓝边构成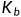 ,所以
,所以 。
。
若 和
和 都是偶数,
都是偶数,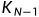 中,假设所有顶点关联的红边数为奇数,则所有顶点关联的红边数之和不为整数,矛盾,所以一定有一个顶点a关联的红边数为偶数,所以a关联的
中,假设所有顶点关联的红边数为奇数,则所有顶点关联的红边数之和不为整数,矛盾,所以一定有一个顶点a关联的红边数为偶数,所以a关联的 条边,要么至少有
条边,要么至少有 条红边,要么至多
条红边,要么至多 条红边(则至少
条红边(则至少 条蓝边),这时我们就可以通过上面的方法证明
条蓝边),这时我们就可以通过上面的方法证明 。
。
拉姆齐数的推广
将红蓝两色推广为任意k种颜色,则 ,...,
,..., 表示的是最小整数使得完全图
表示的是最小整数使得完全图 存在
存在 颜色的
颜色的 ,或者存在
,或者存在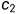 颜色的
颜色的 ,...,或者存在
,...,或者存在 颜色的
颜色的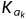 。
。
易证:
 ,...,
,..., ,...,
,...,
 ,...,
,..., ,...,
,..., +
+ ...,
..., ...
... ...,
...,
Schur定理
设 ...,
...,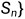 为集合
为集合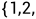 ...,
..., 的划分,则存在i,使得
的划分,则存在i,使得 有三个数
有三个数 (不一定不相同),
(不一定不相同), 。其中
。其中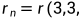 ...,
..., ,n个3。
,n个3。
证明:假设 ...,
..., ,并且
,并且 ,则在
,则在 中,将
中,将 染为i颜色。则在
染为i颜色。则在 中存在同色三角形,设为ab,bc,ac,令
中存在同色三角形,设为ab,bc,ac,令 ,则
,则 ,并且
,并且 。
。
拉姆齐定理
设 ...,
...,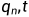 ,且
,且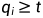 ,则必存在最小正整数
,则必存在最小正整数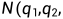 ...,
..., ,
,
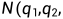 ...,
..., ,
,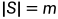 ,使得S中的
,使得S中的
 个元素中的所有t元子集在第一个盒子中,或者
个元素中的所有t元子集在第一个盒子中,或者 个元素中的所有t元子集在第二个盒子中,...,或者
个元素中的所有t元子集在第二个盒子中,...,或者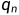 个元素中的所有t元子集在第n个盒子中。
个元素中的所有t元子集在第n个盒子中。
t=1时,表示的是广义鸽巢原理,所有元素为鸽子,所有盒子为鸽巢,则N为最小整数使得 个元素中的所有t元子集在第一个盒子中,或者
个元素中的所有t元子集在第一个盒子中,或者 个元素中的所有t元子集在第二个盒子中,...,或者
个元素中的所有t元子集在第二个盒子中,...,或者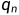 个元素中的所有t元子集在第n个盒子中。
个元素中的所有t元子集在第n个盒子中。
t=2时,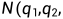 ...,
...,

 ...,
...,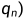 ,二元子集表示为边,盒子表示为颜色,则N为最小整数使得
,二元子集表示为边,盒子表示为颜色,则N为最小整数使得 完全图一定出现第一种颜色的
完全图一定出现第一种颜色的 ,或者第二种颜色的
,或者第二种颜色的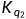 ,...,或者第n种颜色的
,...,或者第n种颜色的 。
。
易证:
























 6万+
6万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








