Fast Fourier Transform （快速傅里叶变换）

数学基础：

通常表示一个多项式我们使用系数表示法：

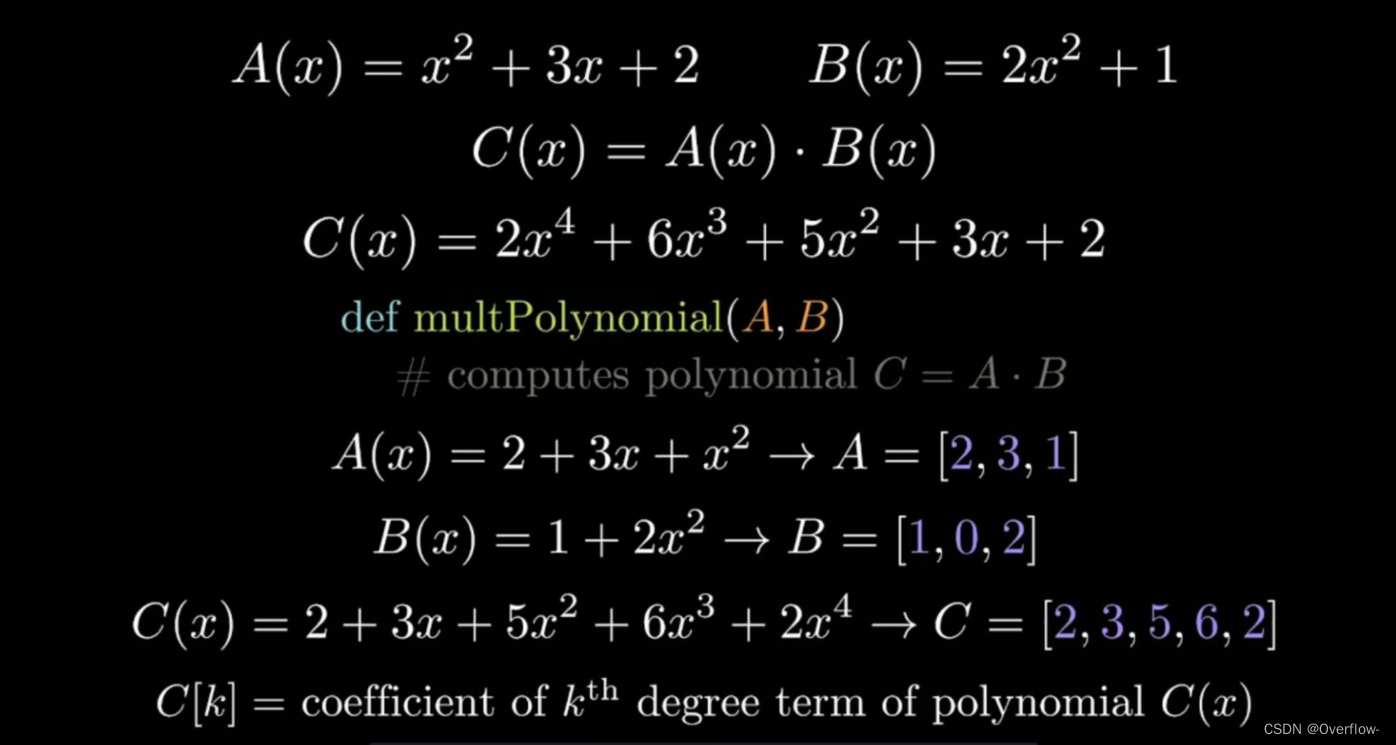
但是在使用系数表示法时我们无法很有效地求解A（x）*B（x），通常我们利用乘法的分配律多次交叉相乘得到积函数的系数，对于两个DgreeBound为n的函数来说总体时间复杂度达到了O（n²）。我们能否对这个算法做出改进？

实际表示多项式的方法其实有很多种，我们现取多项式的点表示法来计算函数的积。

 我们熟知两点确定一条直线，事实上对于高阶多项式有相同的结论：即任一n阶多项式都由d+1个不同点唯一确定。

 线性方程组可以写成矩阵-向量形式：

 这个系数矩阵为范德蒙矩阵，只要x0-xd不相同，则该矩阵可逆，也即这n+1个点可以唯一确定这n个系数。

 那么如果我们要计算两个二阶多项式的乘法，需要各取5个点并据此计算出积函数上的5个点。

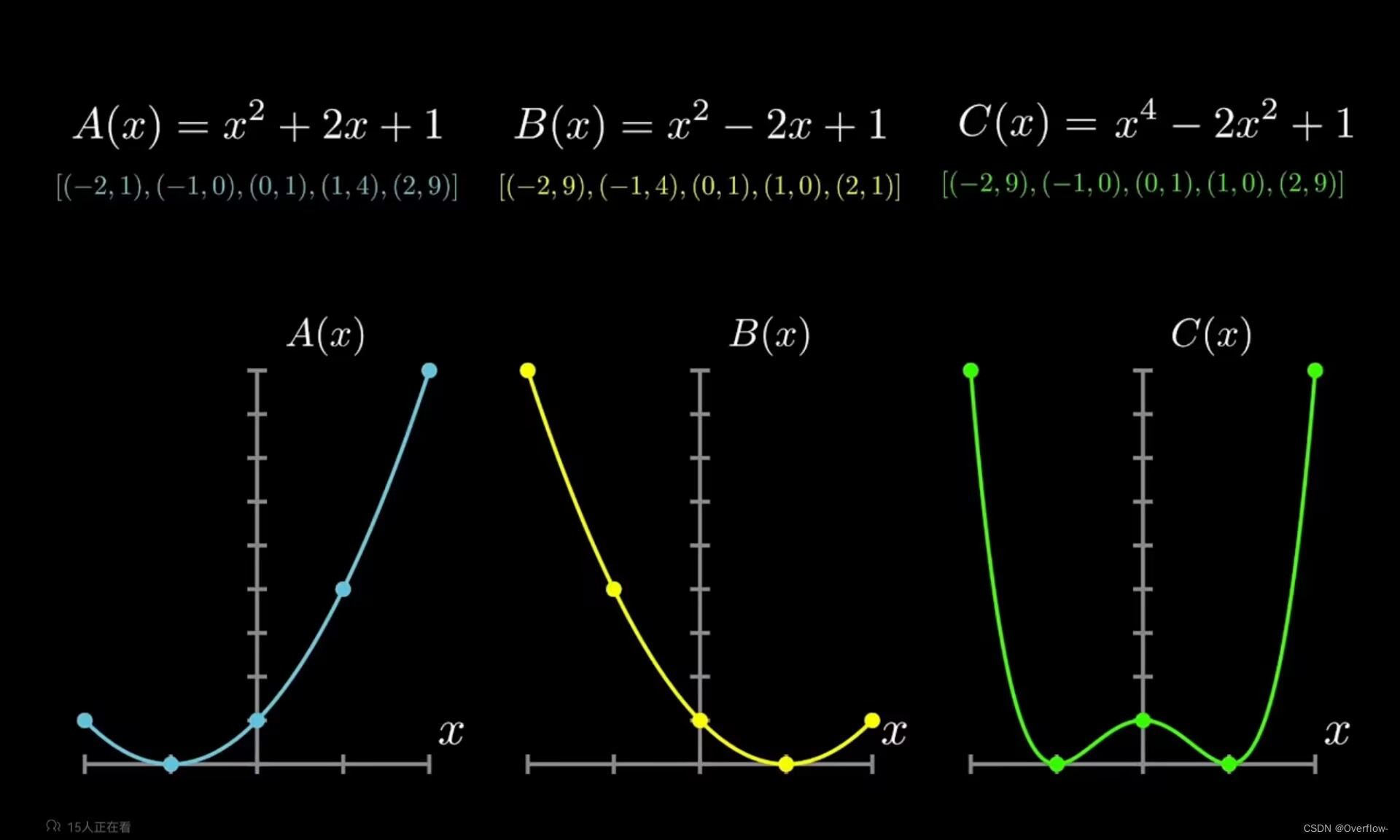
 只需要O（n）就可以得到C上的5个点。

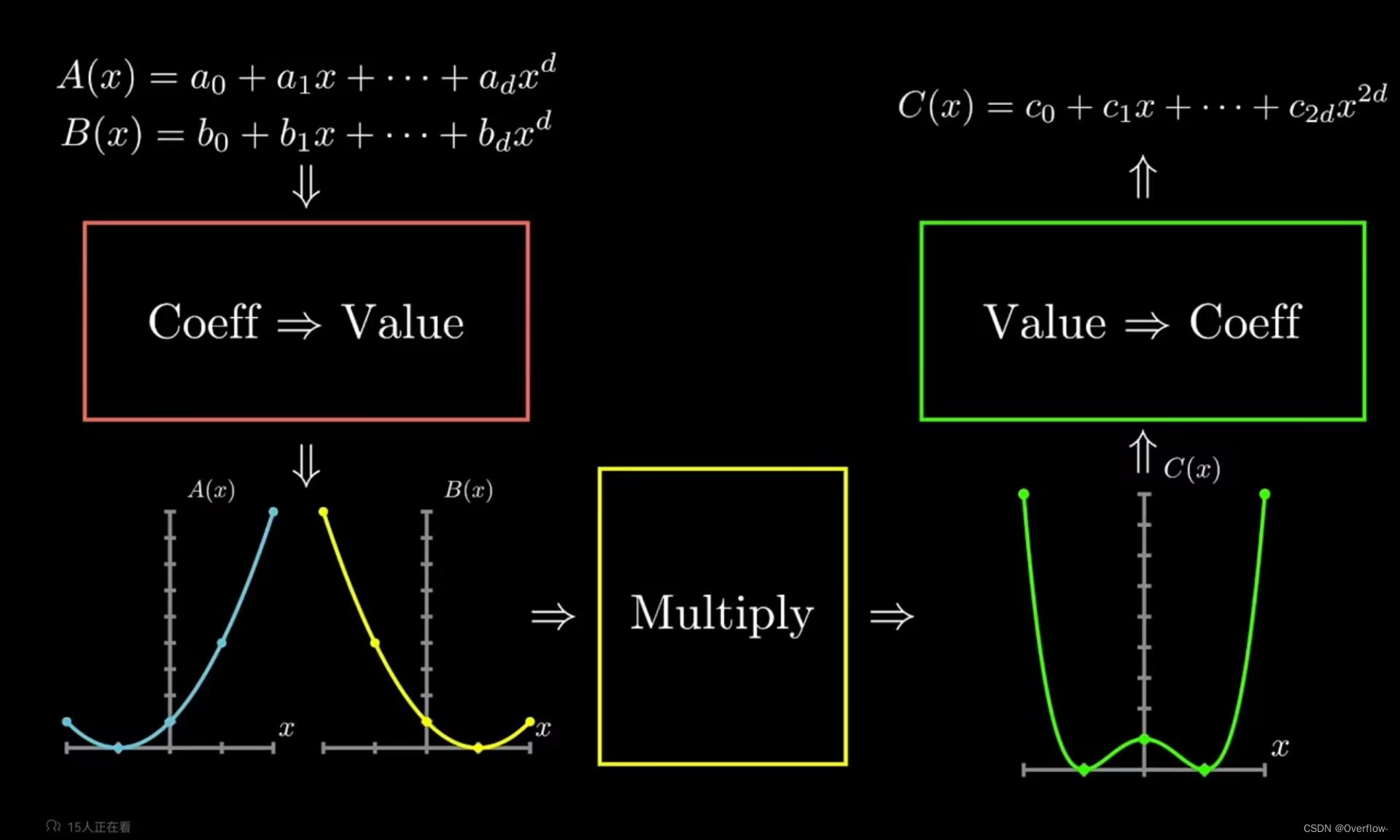
 现在我们有了求解问题的大概方向。但事实上我们缺的是Coeff到Value或反之的方法。

Coeff->Value 求值：

最直接的想法就是在x轴随机上带入n（n>=d+1)这么多个点去计算。然而对于一个d阶多项式来说，每个点的计算都是O（d），加起来变成O（nd）>=O（d²）。这个时候我们就回到了原点……所以现在的问题是能不能整个快的？

我们考虑这个多项式：y=x²。对于这样一个偶函数如果我们要取8个点，应该选择哪些点呢？当然是对称着选，这样能够减少一般的计算耗时。

对于一个普通的多项式，我们该如何选点？

很简单，将多项式进行奇偶拆分。我们将奇函数部分的x提取出来，括号里正是两个偶函数。 

我们在对称着选点进行计算的时候将因为函数值overlap（重叠）而得到极大的便利。同时，我们可以把两个部分都看作DegreeBound为3的函数，比原来的6少了一半。我们可以将这种思想推广到DB为n+1时的情况：

 对于这两个只有一般阶的多项式，我们相当于再次陷入两个函数的求值问题！不过我们这次需要计算给定点的平方（xi²）的函数值。不过我们此时只需要计算n/2个点就可以解决问题。（递归起来了~）

 重新梳理一下，想要求一个n阶多项式的系数，我们只需要关于y轴对称地取n/2个点并对函数进行奇偶的拆分，计算出两部分的函数值，然后合并得到原函数的点表达式。

时间复杂度分析： 如果这一切都能走通，两个子问题的规模为原先的一半，得到两个多项式的函数值序列之后我们只需要O（n）的时间进行合并，T（n）=2T（n/2)+O(n)，时间复杂度仅为O（nlogn）。

然而分析到现在我们忽略了一个重要的问题：在递归步骤，我们假设了每个多项式使用相反数对来求值，然而对两个子问题而言，每个求值点都是平方数大于等于0，所以递归并不成立（悲

 所以我们现在的问题变成了能否将这些新的求值点也搞成相反数？只有一条路可以走：我们把这些点搞成复数！我们还希望挑一些复数，使得它们平方之后依然是正负成对出现的。怎么取呢？我们可以通过一个例子逆向得到解答：

 依靠我们之前的想法进行取点，可以得到上图的树。

 如果我们将x1取为1，更新这个树，显然x2我们将取成纯虚数 i 。从另一个角度看，我们实际上是解了一个方程：X^4=1。因为我们知道最上面的四个数都应该满足其四次方等于1.事实上我们知道这个方程有4个不同的解。也许我们已经找到了解题方法，现在需验证能否推广：

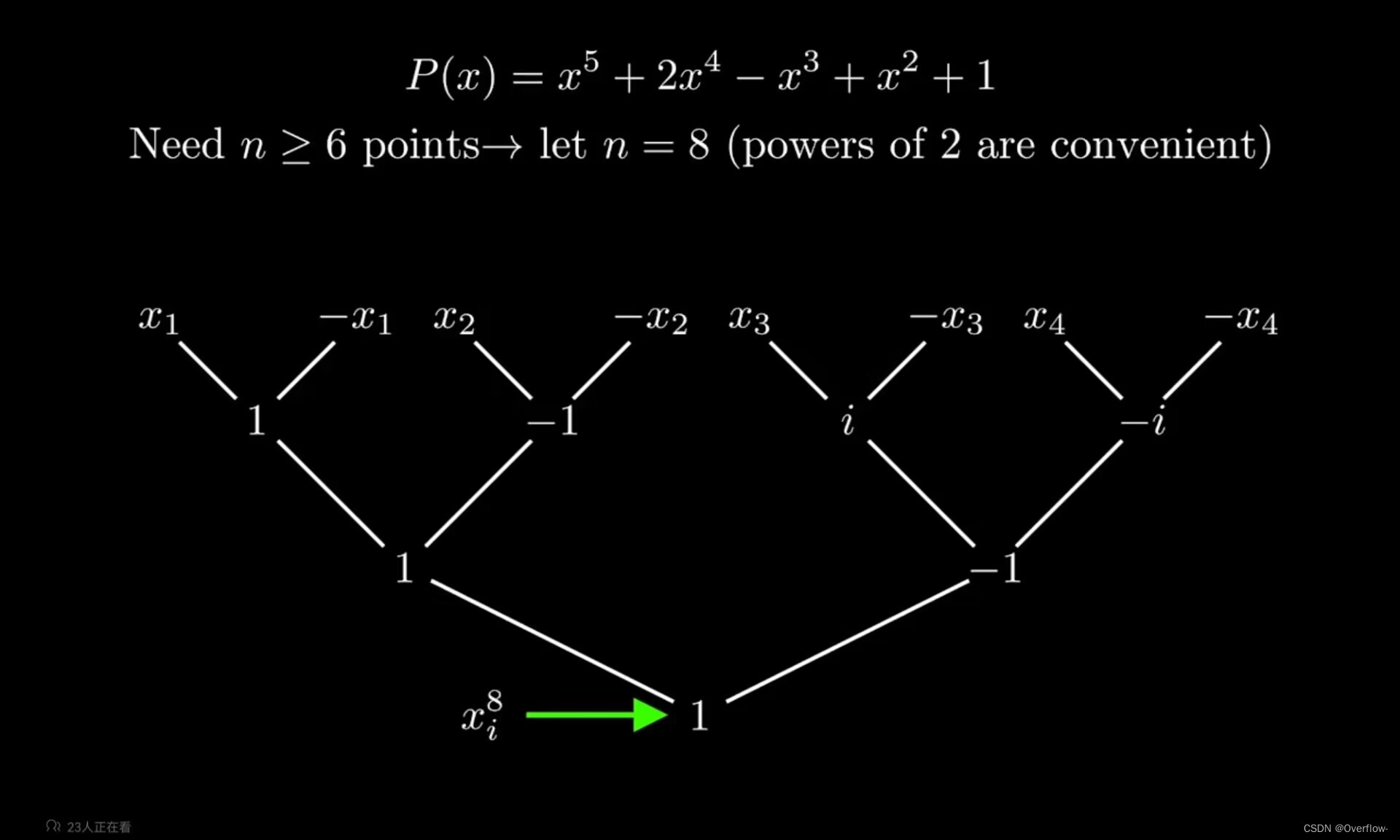
求解这个5阶多项式的系数，我们需要至少6个点。因为我们递归每次需要的点的个数是减半的，所以我们不如直接取一个2的次方数8。现在我们需要寻找8个数，从而形成4个正负对，并保证每个数字的8次方都是1。显然这8个数是1的8个8次方根~

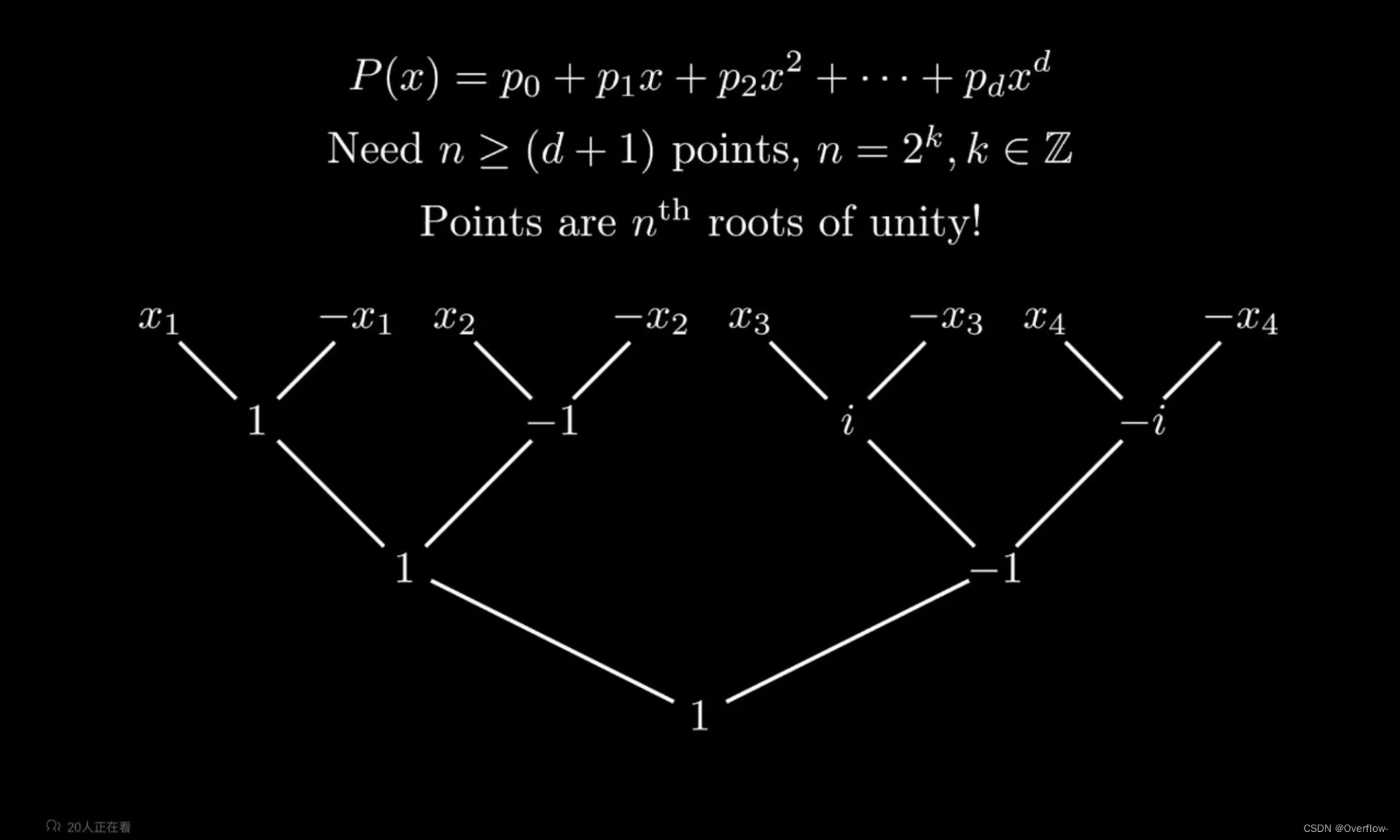
 我们推广到d阶多项式，那么我们要找n个点（n>=d+1)并且n是2的幂次。这些点就应当是1的n个n次方根。

我们再详细探讨一下为什么我们要找的数恰好就是它们。

 1的n次方根可以被解释为复平面上沿着单位元等距排布的一系列点（复数的三角表示），任一相邻两点的夹角为2pi/n。这些点的最简便的表示方法就是用欧拉公式写作复指数的形式。我们定义ω等于exp（2pi*i/n），那么不同的i取值就代表了不同的单位复n次方根（下图的黄点）

所以当我们说想求1的n次方根时，我们实际上是在1，ω，……，ω^(n-1)上求值。主要有两个原因挑选他们用于递归过程：首先我们要求取的点是正负成对的，而这里的ω^(j+n/2)= - ω^j恰好是这样一对。

 另外一点，当我们把第一次取的点平方并考虑对应的递归低阶奇/偶函数时，下图右表现了平方以后的点在复平面上的分布，也就是1的n次方根的另外一个好性质平方以后我们得到的正好是n/2个n/2次方根，它们也是正负配对的，完美适配递归。我们再平方就可以得到n/4个n/4次方根，适用于下一层的递归，直到我们只剩下最后一个点。

 现在我们终于可以介绍FFT算法了：

算法输入为多项式的n个系数p0，p1，……，pn，n是2的幂次；

我们取ω=exp（2pi*i/n）代表1的n次方根，递归的底层情况是n=1，此时我们只在一个点求多项式的值。而递归的主体就是把多项式拆成奇偶两部分，分别调用FFT函数两次（此时两个子多项式函数都是n/2阶的，所以对应的求值点将是1的n/2次方根）。

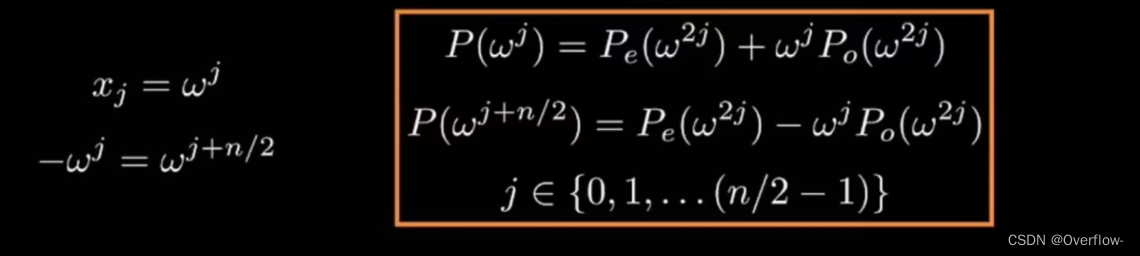
 有一个很nice的事实：ye和yo上的第j个元素正好对应了pe(ω^(2j))和po(ω^(2j))

 这样便于我们写程序。最终FFT输出的是原多项式在n个单位n次方根上的值。现在我们可以尝试撰写伪代码TuT

伪代码：

 这么多点子最后汇聚成了这11行优雅的代码~

 再回头我们还剩下一项工作：把值表示转换为系数表示。我们一般使用插值法解决。实际上求值和插值是紧密相连的，回忆起我们之前可以把函数值阵列表示成矩阵-向量形式：

 而x^k即ω^k。即

 这个系数矩阵我们称之为离散傅里叶变换（DFT）矩阵。（大部分教科书都将FFT描述成快速计算DFT和向量乘法的算法）

而我们的插值求系数也很好理解——不就是给DFT求了个逆么！

 实际上就长这样：（省略了许多代数）

 看起来几乎一模一样，我们只需要把原来的ω换成1/n*ω^(-1)即可。所以我们在插值上也可以套用FFT：

 在反过来求系数的时候使用逆FFT算法，但是punchline在于逆FFT和FFT的操作几乎一致，不过ω换了个值罢了。

 看看伪代码，我们只需要在左边的基础上改两行：ω的赋值、yeyo的递归调用。

 我们用了四个很nb的创新点才将FFT算法完整的写出来~优雅，实在是太优雅了！