N阶行列式求值的详细讲解(C语言)(降阶法)(函数递归)

//2023年06月03日：更新c++代码，使用预编译指令pragma小幅优化性能，更改文章部分内容

//2022年10月03日：内容部分修改，加附程序运行展示

//2022年07月19日：小修小改

//2022年06月25日 : 更新了一些注释

正文：一般比较常见的是3阶和4阶的行列式，3阶行列式可以很方便的直接算出结果，而4阶的行列式却无法运用和3阶行列式类似的公式直接进行计算，必须用降阶法或者其他方法来求解。那么当行列式的阶数是5阶甚至6阶呢？计算的复杂难度无疑是以???级别上涨的，就算真的算出了结果，相信这个过程也会让你回味无穷

声明:以下文章中涉及动态内存分配，为求方便，笔者将用数组这个不那么准确但更好理解的方式代为称呼

以下，为详细讲解：

主要思路是降阶法， 降阶法(按行或列展开)在此不多赘述，相信搜索引擎可以给你一个满意的答案

头文件: stdio.h 和 stdlib.h

主函数部分:

int main(void)
{
    int order;
    printf("Please enter determinant order:\n");
    scanf("%d", &order);

    int *D = InputData(order);
    int Rslt = Reduction(D, order);

    printf("Result:%d", Rslt);

    free(D);

    return 0;
}

order意为行列式阶数；printf的语句意思为请输入行列式的阶数；函数InputData用于录入行列式的各个元素并返回用于储存数据的数组的首地址；D为指向数组首地址的指针，同时也代表了行列式 (D取自英文单词determinant首字母) ；Rslt为行列式计算结果；函数Reduction代表用降阶法计算行列式并返回结果，很显然，通篇文章的精华就在这个函数里，笔者也会花费大量篇幅进行讲解。

函数部分:

int *InputData(int order)
{
    int Row, Col;
    int *D = (int *)malloc(sizeof(int) * order * order);

    printf("Please enter the elements of the determinant:\n");
    for (Row = 0; Row < order; Row++)
        for (Col = 0; Col < order; Col++)
            scanf("%d", D + Row * order + Col);

    return D;
}

//所有传入此函数的行列式都按第一行展开
int Reduction(int *D, int order)
{
    int Rslt = 0;
    if(order>3)
    {
        //当前行列式将要省略的列的列号
        int Col;

        for (Col = 0; Col < order; Col++)
        {
            //此处创建余子式数组
            int *Cofactor = (int *)malloc(sizeof(int) * (order - 1) * (order - 1));
            
            //余子式元素的下标，用于余子式数组元素的赋予
            int pos = 0;

            //用于遍历当前行列式的行号和列号
            int row, col;
            
            //由于按第一行展开，所以遍历时直接从第2行(数组下标为1)开始
            for (row = 1; row < order; row++)
                for (col = 0; col < order; col++)
                {
                    //当遍历行列式的列号与要省略的列号相同时，判定当前元素非余子式元素，直接跳                               
                    //过，进入下一次循环
                    if(col==Col)
                        continue;

                    //否，则余子式数组下标加一，并将行列式当前元素值赋予创建的余子式数组
                    else
                        Cofactor[pos++] = D[row * order + col];
                }
            //余子式符号初始为正
            int sign = 1;

            //若下标为复数(代表行列式列标为单数)，则取负号
            if(Col % 2)
                sign = -1;

            Rslt += D[Col] * sign * Reduction(Cofactor, order - 1);
            free(Cofactor);
        }
    }

    //当阶数小于三时直接用公式计算出结果
    else
    {
        switch(order)
        {
            case 1:
                Rslt = D[0];
                break;
            case 2:
                Rslt = D[0] * D[3] - D[1] * D[2];
                break;
            case 3:
                Rslt = (D[0] * D[4] * D[8] + D[1] * D[5] * D[6] + D[2] * D[3] * D[7] -
                        D[2] * D[4] * D[6] - D[1] * D[3] * D[8] - D[0] * D[5] * D[7]);
                break;
        }
    }
    return Rslt;
}

函数InputData很容易实现，在此不过多赘述。(row和col分别代表行和列的意思)

函数Reduction大体分为两部分：

part1：当阶数order小于等于3时（阶数为1或2或3时），直接利用公式导出结果。

part2：当阶数大于3时，反复调用函数Reduction进行降阶处理。具体为：先创建一个 n-1 阶的余子式数组(Cofactor)，从原行列式中找出属于该余子式的元素并由cofactor储存，然后进行余子式符号(sign)的判定，然后用Rslt加上 "元素乘以对应余子式再乘以符号" 的值，最后释放掉申请的数组cofactor。由于一个 n 阶行列式按某行展开后有n个余子式，所以重复以上过程n次，Rslt加了n次数值后，其结果就为行列式的值。

4阶行列式求解过程详解:

首先，以符号 “D” 代表原行列式，则原行列式各元素编号如下（申请的内存为n*n，下文中的余子式数组同理）

D0      D1      D2      D3  

D4      D5      D6      D7  

D8      D9      D10    D11

D12    D13    D14    D15

然后再申请一个(n-1)*(n-1)大小的余子式数组 (cofactor) , 将原行列式中的对应元素赋予它(本文中每个传入Reduction函数的行列式都是按第一行展开)

以符号 “C” 代表余子式，那么D0的余子式各元素编号为：

C0  =D5  ,  C1  =D6  ,  C2  =D7  ,

C3  =D9  ,  C4  =D10,  C5  =D11,

C6  =D13,  C7  =D14,  C8  =D15,

确定符号sign之后将余子式数组C传进Reduction函数中计算结果并返回，然后进一步处理后被Rslt加上。

D1,D2,D3的余子式同理，最后的Rslt就为行列式值。

总结一下就是：先将 n 阶行列式通过Reduction函数化为 n-1 阶行列式, 然后 n-1 阶行列式又通过Reduction函数化为 n-2 阶行列式，然后 n-2 阶行列式又通过Reduction降阶，直到阶数化为 3 时用公式计算出结果，然后层层返回各阶余子式结果Rslt，最后加回到 n 阶的Rslt中得出结果，其实也就是函数递归。

PS：虽然递归看起来很舒服，但是对内存占用极大，当处理的数据规模一大起来可能内存就爆了

在这里贴一个网站，可以在线免费计算50阶及以下的行列式，链接:在线求行列式的值

您可以比较本文中的程序的计算结果与该网站的计算结果，若有bug欢迎在评论区提出

再附一个5阶行列式：

5 8 9 4 5
7 8 9 2 1
3 2 1 4 5
8 9 7 5 1
1 2 4 5 7

结果为：972

附程序运行过程展示：

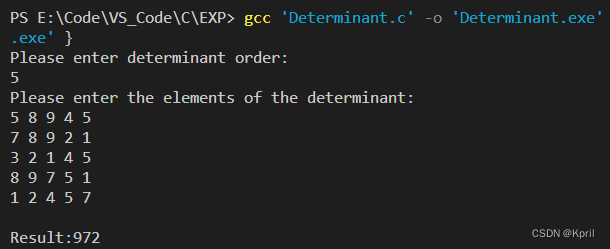
 先输入行列式阶数，然后输入行列式的元素，每个元素用空格或者回车进行间隔，当最后一个元素输入完毕则输出结果

---

C++代码（其实只是简单的在C语言的基础上改了改）：

#include <iostream>
#pragma GCC optimize(2)
#define ent '\n'
using ll = long long;
using namespace std;

ll* InputData(ll order);
ll Reduction(ll* D, ll order);

int main(void) {
  ll order;
  // cout << "Please enter determinant order:" << ent;
  cin >> order;

  ll* D = InputData(order);
  ll Rslt = Reduction(D, order);

  // cout << ent << "Result:" << Rslt;
  cout << Rslt;

  delete[] D;
  return 0;
}

ll* InputData(ll order) {
  ll Row, Col;
  ll* D = new ll[order * order];

  // cout << "Please enter the elements of the determinant:" << ent;
  for (Row = 0; Row < order; Row++)
    for (Col = 0; Col < order; Col++)
      cin >> D[Row * order + Col];

  return D;
}

ll Reduction(ll* D, ll order) {
  ll Rslt = 0;
  if (order > 3) {
    ll Col;
    for (Col = 0; Col < order; Col++) {
      ll* Cofactor = new ll[(order - 1) * (order - 1)];
      ll pos = 0;
      ll row, col;
      for (row = 1; row < order; row++)
        for (col = 0; col < order; col++)
          if (col == Col)
            continue;
          else
            Cofactor[pos++] = D[row * order + col];

      ll sign = 1;
      if (Col % 2)
        sign = -1;

      Rslt += D[Col] * sign * Reduction(Cofactor, order - 1);
      delete[] Cofactor;
    }
  } else {
    switch (order) {
      case 1:
        Rslt = D[0];
        break;
      case 2:
        Rslt = D[0] * D[3] - D[1] * D[2];
        break;
      case 3:
        Rslt = (D[0] * D[4] * D[8] + D[1] * D[5] * D[6] + D[2] * D[3] * D[7] -
                D[2] * D[4] * D[6] - D[1] * D[3] * D[8] - D[0] * D[5] * D[7]);
        break;
    }
  }
  return Rslt;
}

目前能在一秒内跑出结果来的最大阶数是11阶（处理器频率2.4Ghz，内存8GB），12阶的测试则是6s左右。毕竟时间复杂度高达O(n!)，只能1s内计算出11阶以内的行列式是符合预期的，因为 11! 比4e7小一些，12! 比5e8小一些，一般认为1e8左右的计算次数能在1s内出结果

开了pragma优化后11阶行列式能在0.5s左右出结果，没开则是0.7s左右，28%左右的性能提升