C语言用代数余子式计算行列式

是元笙阿

已于 2022-12-25 22:31:26 修改

阅读量2.3w

点赞数 12

分类专栏： # C语言线性代数文章标签：线性代数矩阵 c语言

于 2022-06-08 15:21:24 首次发布

本文链接：https://blog.csdn.net/why1472587/article/details/125105250

版权

C语言线性代数专栏收录该内容

11 篇文章

订阅专栏

本章主要介绍利用代数余子式计算行列的原理及代码实现

除了代数余子式法，其他计算行列式的方法如下：

1）利用高斯法计算行列式

2）利用LU分解法计算行列式

1.代数余子式计算行列式的原理

注意：行列式一定是方阵！

二阶行列式计算

杀戮法：

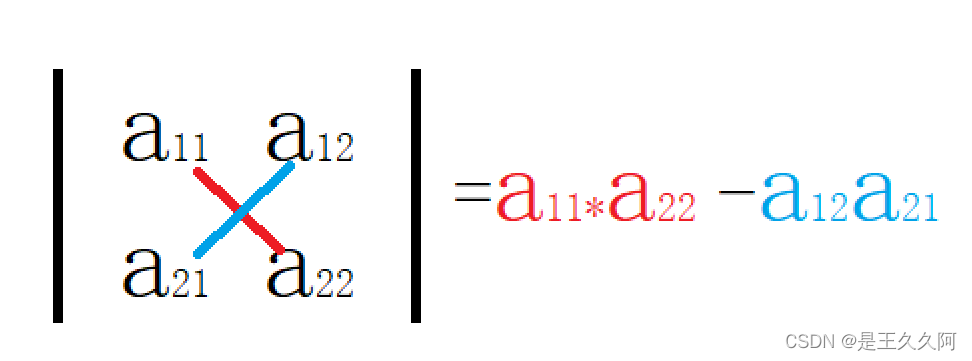
二阶行列式的计算方法非常简单，主对角线元素相乘—副对角线元素相乘，故又称杀戮法。

三阶行列式计算

划线法：

划线法如下图所示

按定义计算

计算行列式时，可以将其按行或列展开进行计算

以三阶行列式为例：

将行列式A按第一行展开：

其中，Aij为aij的代数余子式（i为行号，j为列号），例如：A11为a11的代数余子式。

代数余子式的计算方法：

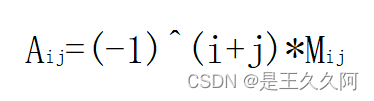
其中，(-1)^(i+j)表示为-1的i+j次方，用来决定代数余子式的正负，Mij为余子式。

余子式：

行列式去其i行j列，剩下的元素组成一个新的行列式，该矩阵为aij的余子式。

例如，a11的余子式为：

去其第一行第一列，剩下的元素按照现有的排列组合成新的行列式。

在计算行列式的值时，我们可以选择0多的那一行和那一列进行展开，大大缩减计算量。

2.代码实现

核心思想：

当我们求高阶行列式的值时，可以利用求代数余子式的方式将求高阶行列式逐步转换为求低阶行列式的问题。利用递归的思想可以解决此类问题，将大事化小，小事化了。

输入矩阵main

在C语言中，矩阵可以利用二维数组数组将其存储起来。

当然用数组存放矩阵也有其缺陷：数组的大小是不可以改变的。在没学动态规划之前，可以根据使用的大小开辟足够大的内存空间，以此来应对该问题。

在输入行列式的时候，还需要确定其阶数n才能进行计算。

#include <stdio.h>
#include <math.h>
#include<assert.h>

#define COL 10//为二维数组开辟的最大内存
int main()
{
	int arr[COL][COL] = { 0 };
	int i = 0, j = 0;
	int n = 0;//阶数
	printf("行列式阶数:>");
	scanf("%d", &n);
	printf("请输入行列式:>\n");
	for (i = 0; i < n; i++)
	{
		for (j = 0; j < n; j++)
		{
			scanf("%d", &arr[i][j]);
		}
	}
	printf("%d", Det(arr, n));
}

行列式的计算Det

因为1阶行列式不用计算，就是其本身，而3阶、2阶的行列式又可以根据划线法和杀戮法计算，这里可以将递归的条件设置为n>3，只有四阶及以上的行列式才进行递归，四阶以下的行列式直接计算得出结果。

在行列式计算前，为了保证数组的安全性，在接收数组的时候加上const，保证数组在函数内部无法修改。
行列式的阶数只有大于等于1时才有意义，在函数开头利用assert断言n是否大于0：条件为真函数运行，条件为假assert则会报警告，assert需包含头文件。

int Cof(const int arr2[COL][COL], int i, int n);//声明：计算行列式

//计算行列式
int Det(const int arr[COL][COL], int n)
{
	assert(n > 0);
	int sum = 0;
	int i = 0;
	if (n == 1)//1阶行列式直接得出结果
	{
		sum = arr[0][0];
	}
	else if (n == 2)
	{
		sum = arr[0][0] * arr[1][1] - arr[0][1] * arr[1][0];//杀戮法求解
	}
	else if (n == 3)
	{
		sum = arr[0][0] * arr[1][1] * arr[2][2]
			+ arr[0][1] * arr[1][2] * arr[2][0]
			+ arr[1][0] * arr[2][1] * arr[0][2]
			- arr[0][2] * arr[1][1] * arr[2][0]
			- arr[0][1] * arr[1][0] * arr[2][2]
			- arr[1][2] * arr[2][1] * arr[0][0];//划线法求解
	}
	else
	{
		for (i = 0; i < n; i++)//按第一行展开
		{
			if (arr[0][i] != 0)//展开项不为0才计算
			{
				sum += ((int)pow(-1, i + 2)) * arr[0][i] * (Cof(arr, i, n));//2阶以上继续递归		
			}
			else
				sum += 0;//展开项为0
		}
	}
	return sum;
}

余子式Cof

接收Det函数传过来的二维数组，取其行列，剩下的元素组成新的二维数组再传给Det函数。两个函数相互调用，直到阶数小于4。

int Det(const int arr[COL][COL], int n);//声明：计算代数余子式

//找到余子式
int Cof(const int arr[COL][COL], int i, int n)
{
	assert(n > 0);
	int k = 0;
	int j = 0;
	int arr2[COL][COL] = { 0 };
	for (k = 0; k < n - 1; k++)//去除0行i列，剩下的组成新的矩阵
	{
		for (j = 0; j < n - 1; j++)
		{
			if (j < i)
			{
				arr2[k][j] = arr[k + 1][j];
			}
			else
			{
				arr2[k][j] = arr[k + 1][j + 1];
			}
		}
	}
	return Det(arr2, n - 1);
}