3. 解谜游戏

小张是一个密室逃脱爱好者，在密室逃脱的游戏中，你需要解开一系列谜题最终拿到出门的密码。现在小张需要打开一个藏有线索的箱子，但箱子上有下图所示的密码锁。

每个点是一个按钮，每个按钮里面有一个小灯。如上图，红色代表灯亮，白色代表灯灭。每当按下按钮，此按钮的灯以及其上下左右四个方向按钮的灯状态会改变（如果原来灯亮则灯灭，如果原来灯灭则灯亮）。如果小张通过按按钮将灯全部熄灭则能可以打开箱子。

对于这个密码锁，我们可以先按下左上角的按钮，密码锁状态变为下图。

再按下右下角的按钮，密码锁状态变为下图。

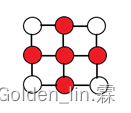
最后按下中间的按钮，灯全部熄灭。

现在小张给你一些密码锁的状态，请你告诉他最少按几次按钮能够把灯全部熄灭。

Input

第一行两个整数

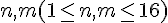
接下来n行，每行一个长度为的01字符串，0表示灯初始状态灭，1表示灯初始状态亮。

Output

一行一个整数，表示最少按几次按钮可以把灯全部熄灭。

Notes

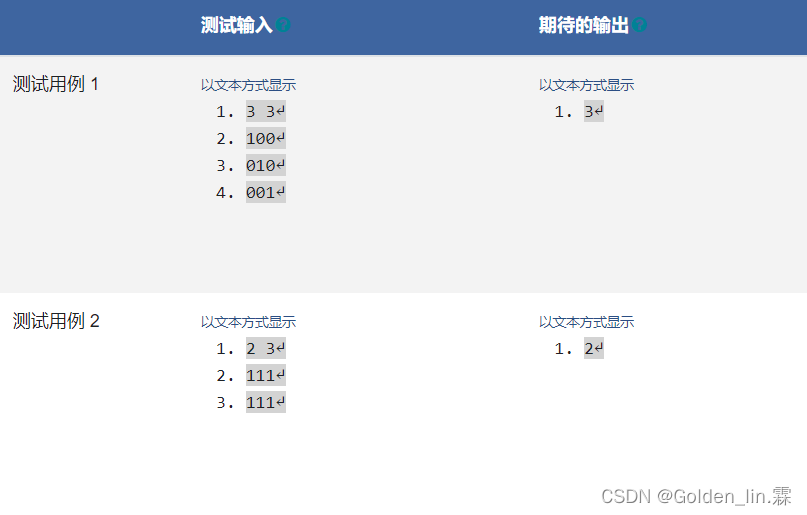
第一个样例见题目描述，第二个样例按左上和右下两个按钮。

 

解题思路：

对题意分析可得，按开关的顺序对答案无影响，故我们可以给他一个顺序方便我们分析。当固定顺序，只能从上到下的行数按开关时，

当第一行确定状态后，第一行所没关闭的灯只能通过第二行来控制，以此类推，第n-1行只能通过第n行控制。

若要将所有灯全部关闭，我们对2~n的操作必然是为了关闭前一行操作后1~n-1剩下的灯，因此当第一行按开关的方案确定后，剩余行按的方案唯一。

所以我们可以枚举第一行状态，并逐行推出每一行状态，最后枚举最后一行判断是否合法，合法则更新当前答案。

枚举第一行的方法我们使用状态压缩的方法，即用一个二进制数来代表开关，比如第i位为1代表第i位为开，第j位为0代表第j位为关，因此0~2^N-1这些数恰好对应第一行的所有状态，我们通过遍历这些二进制数我们就可以轻松且不重复不漏的遍历所有状态了。

#include <cstdio>
#include <cstring>
#include<iostream>
using namespace std;
const int N = 50;
char g[N][N], first[N][N];
int turnx[5] = {-1, 0, 1, 0, 0}, turny[5] = {0, 1, 0, -1, 0};//用数组记录上下左右，方便遍历 
int X,Y;
void tu(int x, int y)
{
    for (int i = 0; i <= 4; i ++ )
    {
        int a = x + turnx[i], b = y + turny[i];
        if (a < 0 || b < 0 || a >= X || b >= Y) continue;
        if(g[a][b]=='1')g[a][b]='0';
        else g[a][b]='1';
    }
}

int main()
{
	int x;
    scanf("%d%d", &X,&Y);
    for (int i = 0; i < X; i ++ ) scanf("%s", first[i]); 
    long long res = 0x7f3f3f3f,ans;
    for (int op = 0; op < (1<<Y); op ++ )//遍历第一行的状态 
    {
        long long cnt = 0;
        memcpy(g, first, sizeof g);
        for (int i = 0; i < Y; i ++ )
            if (op >> i & 1)//1代表开 
            {
                tu(0, i);
                cnt ++ ;
            }
            
        if(X>1)for (int i = 0; i < X-1; i ++ )
            for (int j = 0; j <= Y-1; j ++ )
                if (g[i][j] == '1')//这一行要关闭只能动下一行 
                {
                    tu(i + 1, j);
                    cnt ++ ;
                }
        int p = 1;
        for (int i = 0; i <= Y-1; i ++ )
            if (g[X-1][i] == '1')//判断最后一行的状态 
                p = 0;
        if (p ) res = min(res,cnt);//更新最小值 
    }
    printf("%d\n", res);
    return 0;
}