数据结构与算法实验

实验目的

实验一：

            （1）掌握线性表的实现。

            （2）掌握线性表的应用。

实验二：

（1）掌握栈和队列的实现。

（2）掌握栈和队列的应用。

实验三：

1. 掌握二叉树的实现。
2. 掌握二叉树的应用。

实验四：

1. 掌握图结构的实现。
2. 掌握图结构的应用

实验内容与实验步骤

2.1线性表的应用

(1)我选定了题目一（学生信息的录入）。

(2)定义存储结构：

typedef struct Node {

       double data;

       char subject[30];

       struct Node * next;

}Node;

data储存分数，subject储存科目名称。

1. 基本操作：

a.初始化链表操作initList()，创建一个带头节点的空表并返回表头；

b.往链表里添加元素操作addGrade(Node* list,double score,char subject[30])，将分数为score的subject插入链表里；

c.遍历链表printList(Node* list)，输出链表里所有科目及对应成绩；

d.寻找最高分maxScore(Node* list)和寻找最低分minScore(Node* list)找到分别找到最高分和最低分并输出分数及所属科目；

e.删除科目deleteSubject(Node* list,char* name)，找到并删除名为name的科目及对应分数；

f.求平均分averageScore(Node* list)，求出平均分并输出。

2.2栈和队列的应用

1. 我选择算术表达式求值：利用栈实现一个中缀表达式的求值；
2. 定义存储结构：

typedef struct OPNumber{//操作数栈，存放操作数

       int data;

       struct OPNumber* next;

}OPNumber;

typedef struct OPChar {//操作符栈，存放操作符

       char opChar;

       struct OPChar* next;

}OPChar

1. 基本操作

初始化操作数栈initNumberStack()；

初始化操作符栈 initCharStack()；

判断栈空isNumberStackEmpty()，isCharStackEmpty();

入栈pushNumberStack(),pushCharStack()，采用头插法入栈，出栈时只需弹出头节点地下一节点即可；

出栈popNumberStack(),popCharStack();

获取栈顶getTopOfCharStack(),getTopOfNumberStack();

输入get_input();

计算evaluate_expression()。

2.3 二叉树的应用

(1)存储结构（孩子链表和二叉链表）：

typedef struct Children {

       //孩子在邻接表的位置(头节点的index为链表里节点数量)

       int index;

       //后继结点

       struct Children* next;

}Children;

typedef struct CTBox {

       //节点在的邻接表位置

       int index;

       int perant;

       //数据域

       char name[30];

       int sum;

       //孩子链表

       Children* childrenList;

}CTBox;

typedef struct BNode {

       char name[30] ;

       int sum;

       struct BNode* offspring;//左子树

       struct BNode* sibling;//右子树

}BNode;

（2）操作

创建树initTree（）；

先根遍历preRootTravel();

后根遍历lastRootTravel();

初始化二叉树initBTree();

把树转化为二叉树toBTree();

二叉树的先序、中序、后序遍历preOrder(),midOrder(),lastOrder();

读取queries.txt的查询并给出回答操作getAnswer();

2.4 图结构的应用

（1）存储结构（邻接表）：

typedef struct EBox {//边

       int distance;//距离

       int cost;//费用

       int toVex;//终点顶点位置

       struct EBox* nextEdge;//下一条边

}EBox;

typedef struct VexBox {//结点

       char name[15];

       struct EBox* firstEdge;//第一条出边

}VexBox;

typedef struct Graph {//图

       int edgeNum, vexNum;//边数和结点数

       VexBox AdjList[MAX];//邻接数组

}Graph;

（2）基本操作：

初始化图initGraph();

添加结点间的关系addVexAndEdge();

深度优先遍历DFS();

广度优先遍历BFS();

获取最短路径shortestRoute();

实验环境

操作系统、调试软件名称、版本号，上机地点，机器台号

操作系统：windows11 64位操作系统

调试软件：visual studio2019 4.8.04161

1. 实验过程与分析

实验一

实验过程：

（1）初始化链表：

Node* initList() {

       Node* head = (Node*)malloc(sizeof(Node));

       head->next = NULL;

       head->data = 0;

       strcpy(head->subject, "表头");

       return head;

}

头节点data域存放链表的元素个数，便于在平均数求取时得到科目数量。

（2）插入节点

void addGrade(Node* list, double score, char subjectName[30]) {

       Node* node = (Node*)malloc(sizeof(Node));

       node->data = score;

       strcpy(node->subject, subjectName);

       node->next = list->next;

       list->next = node;

       list->data++;

}

采用头插法插入结点，每添加一个元素，头节点data加一。

（3）输出链表内容

void printList(Node* list) {

       Node* node = list->next;

       printf("成绩如下：\n");

       printf("\n科目\t成绩\n");

       while (node) {

              printf("%s\t%.2f\n", node->subject, node->data);

              node = node->next;

       }

}

（4）计算最高分

void maxScore(Node* list) {

       Node* node = list->next;

       Node* maxNode = node;

       while (node) {

              if (node->data > maxNode->data) {

                     maxNode = node;

              }

              node = node->next;

       }

       printf("\n最高分\n");

       printf("%s\t%.2f\n", maxNode->subject, maxNode->data);

}

找到最低分的科目，并输出其科目名称及分数

（5）计算最低分

void minScore(Node* list) {

       Node* node = list->next;

       Node* minNode = node;

       while (node) {

              if (node->data < minNode->data) {

                     minNode = node;

              }

              node = node->next;

       }

       printf("\n最低分\n");

       printf("%s\t%.2f\n", minNode->subject, minNode->data);

}

找出最低分的科目，并输出科目名称和分数

（6）删除科目

void deleteSubject(Node* list, char* name) {

       Node* p = list;

       Node* node = p->next;

       while (node) {

              if (strcmp(node->subject, name) == 0) {

                     p->next = node->next;

                     free(node);

                     printf("\n删除成功！\n");

                     return;

              }

              p = node;

              node = node->next;

       }

       printf("\n删除失败\n");

}

输入科目名称，在链表中找到并删除科目名称为输入值的结点

（7）计算平均分

void averageScore(Node* list) {

       double sum = 0;

       Node* node = list->next;

       while (node) {

              sum += node->data;

              node = node->next;

       }

       printf("\n平均分：");

       printf("%.2f\n", sum / list->data);

}

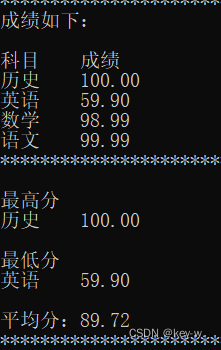
测试用例：

用例编号	用例输入	预计输出	实际输出	测试结果评估
1	语文 100 数学 99 英语 98 化学 50 生物 78	语文 100 数学 99 英语 98 化学 50 生物 78 最高分： 语文 100 最低分： 化学 50 平均分：85.00		输出结果符合预期
2	删除语文	数学 99 英语 98 化学 50 生物 78 最高分： 数学 99 最低分： 化学 50 平均分：81.25		结果符合预期
3	语文 99.99 数学 98.99 英语 59.9 历史 100	语文 99.99 数学 98.99 英语 59.9 历史 100 最高分： 历史 100 最低分： 英语 59.9 平均分：89.72		结果符合预期
4	删除历史	语文 99.99 数学 98.99 英语 59.9 最高分： 语文 99.99 最低分： 英语 59.9 平均分：86.29		结果符合预期

实验二

实验过程：

1. 初始化栈（此为初始化操作数栈）

OPNumber * initNumberStack() {

       OPNumber* numberStack = (OPNumber*)malloc(sizeof(OPNumber));

       numberStack->data = 0;

       numberStack->next = NULL;

       return numberStack;

}

创建一个带头结点地链式栈，并返回头节点，初始化操作符栈类似。

1. 判断栈空（此为操作数栈）

int isNumberStackEmpty(OPNumber* stack) {

       if (stack->next)

              return 0;

       else

              return 1;

}

栈为空，返回1，否则返回0，操作符栈判断方法一样。

1. 入栈（以操作数入栈为例）

void pushNumberStack(OPNumber* stack, int number) {

       OPNumber* node = (OPNumber*)malloc(sizeof(OPNumber));

       node->data = number;

       node->next = stack->next;

       stack->next = node;

}

使用头插法入栈，操作符入栈与此类似；

1. 出栈（以操作数出栈为例）

int popNumberStack(OPNumber* stack) {

       if (!isNumberStackEmpty(stack)) {

              OPNumber* node = stack->next;

              int number = stack->next->data;

              stack->next = stack->next->next;

              free(node);

              return number;

       }

       else

              printf("操作符栈为空\n");

}

栈不为空，则弹出第一个结点，否则出栈失败，操作符出栈与此类似；

1. 获取栈顶

char getTopOfCharStack(OPChar* stack) {

       if (!isCharStackEmpty(stack)) {

              return stack->next->opChar;

       }

       else

              printf("栈为空！\n");

}

得到栈顶元素，用于比较运算符优先级和计算

1. 获取输入

int get_input(int* n)

{

       *n = 0;

       char ch = getchar();

       if (!isdigit(ch))

       {

              *n = ch;

              getchar();

              return true;

       }

       do

       {

              *n = (*n) * 10 + (ch - '0');

              ch = getchar();

       } while (ch != '\n');

       return false;

}

依次获取从控制台输入的字符

1. 计算

int evaluate_expression(OPNumber* numberStack,OPChar* charStack) {

       /* 输入元素 */

       int* element = (int*)malloc(sizeof(int));

       /* 输入元素类型

        * type = true表示输入为运算符

        * type = false表示输入为运算数

       */

       int type;

       /* 出栈元素 */

       int* x = (int*)malloc(sizeof(*x));

       /* 运算出栈元素 */

       int* theta = (int*)malloc(sizeof(int));

       int* a = (int*)malloc(sizeof(int));

       int* b = (int*)malloc(sizeof(int));

       pushCharStack(charStack, '#');

       type = get_input(element);

       *x = '#';

       while (*element != '#' || *x != '#')

       {

              /* 输入不是运算符 */

              if (!type)

              {

                     //操作数入栈

                     pushNumberStack(numberStack, *element);

                     type = get_input(element);

              }

              else

              {

                     *x = getTopOfCharStack(charStack);

                     switch (precmp(*x, *element))

                     {

                     case '<':

                            pushCharStack(charStack, *element);

                            type = get_input(element);

                            *x = getTopOfCharStack(charStack);

                            break;

                     case '=':

                            *x = popCharStack(charStack);

                            type = get_input(element);

                            break;

                     case '>':

                            *theta = popCharStack(charStack);

                            *b = popNumberStack(numberStack);

                            *a = popNumberStack(numberStack);

                            pushNumberStack(numberStack, compute(*a, *theta, *b));

                            *x = getTopOfCharStack(charStack);

                            break;

                     }

              }

       }

       *x = getTopOfNumberStack(numberStack);

       free(element);

       free(a);

       free(b);

       free(theta);

       return *x;

}

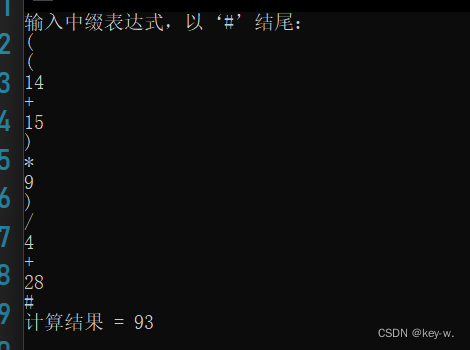
测试用例

用例编号	测试输入	预计输出	实际输出	结果评估
1	14+16	30		结果符合预期
2	（14+16）*3	90		结果符合预期
3	（（14+15）*9）/4+28	93.25		由于程序的数据类型为int，所以小数位被舍去，实验结果较符合预期

实验三

实验过程：

1. 初始化树：

void initTree(CTBox* Tree, char info[][3][30],char buildings[][30],int* many) {

       for (int i = 0; i < Max; i++) {

              Tree[i].index = i;

              strcpy(Tree[i].name, buildings[i]);

              Tree[i].sum = *(many + i);

              Tree[i].childrenList = initChildrenList();

       }

       Tree[0].perant = -1;//根节点无父节点

       for (int i = 0; i < 17; i++) {

              int parent = -1;

              for (int j = 1; j < Max; j++) {

                     if (strcmp(info[i][2], Tree[j].name) == 0) {//儿子

                            for (int k = 0; k < Max; k++) {

                                   if (strcmp(info[i][0], Tree[k].name) == 0) {//父亲

                                          Tree[j].perant = k;

                                          addChild(Tree[k].childrenList, j);

                                   }

                            }

                     }    

              }

       }

}

info为一个通过读取definition.txt构建的二维字符串数组，存储了医院各个建筑的名称、每个建筑数量及其之间的关系；

buildings字符串数组存储了医院的所有不重复建筑名称，many数组为对应的数量。

1. 树的先根遍历

void preRootTravel(CTBox* Tree,CTBox* Root) {//先根遍历

       printf("\t%-30s%d\n", Root->name,Root->sum);

       Children* node = Root->childrenList->next;

       while (node) {

              preRootTravel(Tree, &Tree[node->index]);

              node = node->next;

       }

}

先根遍历树的结点及其数量；

1. 树的后根遍历

void lastRootTravel(CTBox* Tree, CTBox* Root) {//后根遍历

       Children* node = Root->childrenList->next;

       while (node) {

              lastRootTravel(Tree, &Tree[node->index]);

              node = node->next;

       }

       printf("\t%-30s%d\n", Root->name,Root->sum);

}

后根遍历树的结点及其数量；

1. 初始化二叉树

BNode* initBTree(CTBox* Tree) {

       BNode* BTree = (BNode*)malloc(sizeof(BNode));

       BTree->offspring = NULL;

       BTree->sibling = NULL;

       toBTree(Tree, BTree, Tree[0]);

       return BTree;

}

Tree为一个多叉树，调用toBTree方法后将其转为二叉树，并返回根节点地址

1. 把多叉树转二叉树

int toBTree(CTBox* Tree,BNode* BTree,CTBox root) {//多叉树转二叉树

       int i = 0;

       BNode* ptemp;

       strcpy(BTree->name, root.name);

       BTree->sum = root.sum;

       if (root.childrenList->next == NULL) {

              BTree->offspring = NULL;

              return 0;

       }

       BNode* pbnode = (BNode*)malloc(sizeof(BNode));

       BTree->offspring = pbnode;

       toBTree(Tree, pbnode, Tree[root.childrenList->next->index]);//处理左子树

       i = 1;

       ptemp = pbnode;

       Children* node = root.childrenList->next->next;

       while (i < root.childrenList->index && node != NULL) {

              BNode* pbnode = (BNode*)malloc(sizeof(BNode));

              ptemp->sibling = pbnode;

              ptemp = pbnode;

              toBTree(Tree, pbnode, Tree[node->index]);//处理右子树

              i++;

              node = node->next;

       }

       ptemp->sibling = NULL;

       return 0;

}

传入一棵二叉树的根和一个多叉树以及多叉树根，通过递归将其转为二叉树，多叉树的第一个孩子变成二叉树左子树，第二个孩子作为第一个孩子的右子树，以此类推（兄弟变右孩子），直到所有子树都变为二叉树为止。

（6）二叉树遍历（以前序遍历为例，中后序遍历仅访问结点语句位置不同）

void preOrder(BNode* BTree) {//先序遍历

       if (BTree != NULL) {

              printf("\t%-30s%d\n", BTree->name,BTree->sum);

              preOrder(BTree->offspring);

              preOrder(BTree->sibling);

       }

       else {

              return;

       }

}

（7）读取queries.txt的查询并给出回答

void getAnswer(char* questionsFile,CTBox Tree[]) {//读取问题并获得答案

       char question[13][4][30];

       FILE* fp;

       char line[100];

       if ((fp = fopen(questionsFile, "r")) == NULL) {

              printf("Error\n");

              return -1;

       }

       for (int i = 0; i < 13;i++) {

              for (int j = 0; j < 4; j++) {

                     strcpy(question[i][j], " ");

              }

       }

       int index = 0;

       while (!feof(fp) && index <= 13) {//将文件内容读取到info数组里

              fgets(line, 100, fp);

              int t = strlen(line);//逐行读取，存入line里

              if (line[t - 1] == '\n') {//吃掉"\n"

                     line[t - 1] = 0;

              }

              char* str2 = strtok(line, " ");//对line以" "作为分隔符分割

              int j = 0;

              while (j < 4 && str2 != NULL) {

                     strcpy(question[index][j], str2);

                     str2 = strtok(NULL, " ");

                     j++;

              }

              index++;

       }

       fclose(fp);

       answer(question, Tree);

}

void answer(char question[][4][30], CTBox* Tree) {//获取答案

       int sum = 0;

       for (int i = 0; i < 13; i++) {

              if (strcmp(question[i][0], "what") == 0) {

                     for (int j = 0; j < Max; j++) {

                            if (strcmp(question[i][2], Tree[j].name) == 0) {

                                   printf("\n\t(%d)Part %s subparts are:\n",i + 1,Tree[j].name);

                                   Children* node = Tree[j].childrenList->next;

                                   while (node) {

                                          printf("\t\t%d %s\n", Tree[node->index].sum,                                                                                  Tree[node->index].name);

                                          node = node->next;

                                   }

                            }

                     }

              }

              if (strcmp(question[i][0], "how") == 0) {

                     for (int j = 0; j < Max; j++) {

                            if (strcmp(question[i][2], Tree[j].name) == 0) {//孩子

                                   for (int k = 0; k <= j; k++) {

                                          if (strcmp(question[i][3], Tree[k].name) == 0) {//父亲

                                                 sum = getSum(Tree[k], Tree[j], Tree);

                                                 printf("\n\t(%d)%s has %d %s\n",i + 1,Tree[k].name, sum,                                                                Tree[j].name);

                                                 break;

                                          }

                                   }

                            }

                     }

              }

       }

}

运行结果

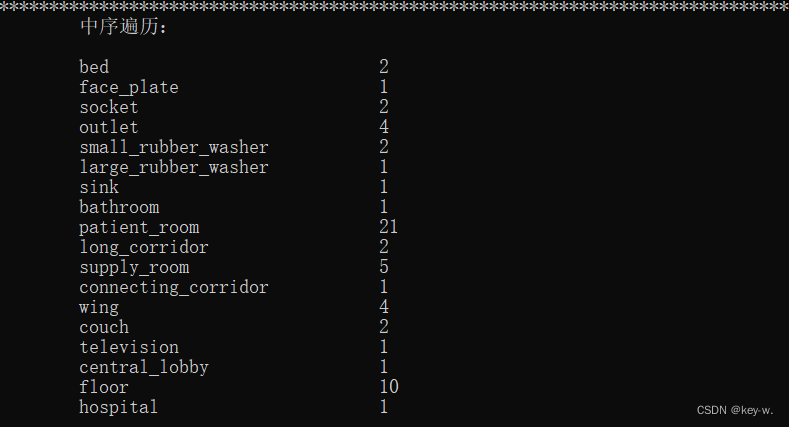
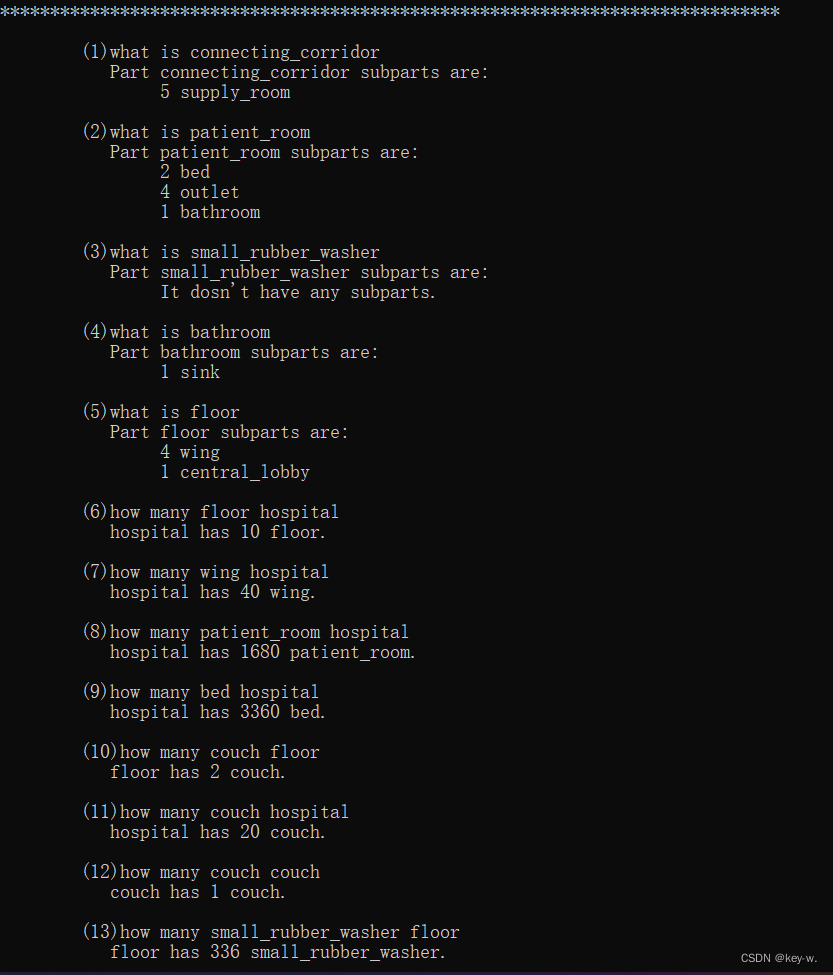
实验四

实验过程：

1. 初始化图（生成孤立结点）

Graph* initGraph(char cities[][15]) {//初始化邻接数组

       Graph* graph = (Graph*)malloc(sizeof(Graph));

       graph->edgeNum = 0;

       graph->vexNum = MAX;

       for (int i = 0; i < MAX; i++) {

              strcpy(graph->AdjList[i].name, cities[i]);

              graph->AdjList[i].firstEdge = initEdgeList();

       }

       return graph;

}

cities为存储城市名称的数组，将其依次赋值给结点的name域；

1. 建立结点间的关系（添加边）

void addVexAndEdge(Graph* graph,char info[][4][15],char cities[][15]) {

       for (int i = 0; i < 54; i++) {

              int start = -1;

              int end = -1;

              for (int j = 0; j < MAX; j++) {

                     if (strcmp(graph->AdjList[j].name, info[i][0]) == 0) {//起点

                            start = j;

                     }

                     if (strcmp(graph->AdjList[j].name, info[i][1]) == 0) {//终点

                            end = j;

                     }

              }

              int cost = atoi(info[i][2]);

              int distance = atoi(info[i][3]);

              addEdge(graph->AdjList[start].firstEdge, cost, distance, end);

              graph->edgeNum++;

       }

}

info为存储结点名称、结点间关系和边的权值的数组，cities为存储城市名称的数组；

1. 深度优先遍历

void DFS(Graph* graph,int* isvisted,int* index) {//深度遍历连通的19个城市

       if (isvisted[*index] != 0) {

              return;

       }

       printf("\t\t%s\n", graph->AdjList[*index].name);

       isvisted[*index] = 1;

       EBox* node = graph->AdjList[*index].firstEdge->nextEdge;

       while (node) {

              *index = node->toVex;

              DFS(graph, isvisted, index);

              node = node->nextEdge;

       }

}

void DFSAll(Graph* graph,int* visited) {//深度遍历所有城市

       int order = 0;

       DFS(graph, visited, &order);

       EBox* node = graph->AdjList[20].firstEdge->nextEdge;

       while (node) {//遍历孤立的两个城市

              printf("\n\t\t%s\n", graph->AdjList[20].name);

              visited[20] = 1;

              printf("\t\t%s\n",  graph->AdjList[node->toVex].name);

              visited[node->toVex] = 1;

              node = node->nextEdge;

       }

}

采用递归对每个城市深度优先遍历

1. 广度优先遍历

void BFS(Graph* graph, int* visited,int index,Queue* Q) {//广度优先遍历一个点   

       printf("\t\t%s\n", graph->AdjList[index].name);//访问节点

       visited[index] = 1;

       inQueue(Q, graph->AdjList[index]);//节点入队

       EBox* p;

       while (!isEmpty(Q)) {

              p = graph->AdjList[index].firstEdge->nextEdge;

              deQueue(Q);//节点出队

              while (p) {

                     if (visited[p->toVex] == 0) {

                            printf("\t\t%s\n", graph->AdjList[p->toVex].name);

                            visited[p->toVex] = 1;

                            inQueue(Q, graph->AdjList[p->toVex]);//入队相关结点

                     }

                     p = p->nextEdge;

              }

       }

}

建立辅助数组visited记录结点是否被访问过，假设对结点i进行广度优先遍历，则先访问结点i，将结点i入队，再将visited[i]标记为true,然后弹出队首，访问i能直接到达且还未被访问过的结点，入队，然后修改visited相应的元素。

void BFSAll(Graph* graph,int* visited) {//广度优先遍历所有结点

       for (int i = 0; i < 22; i++) {

              visited[i] = 0;

       }

       Queue* Q = initQueue();

       for (int i = 0; i < graph->vexNum; i++) {

              if (visited[i] == 0) {

                     if (i == 20) {

                            printf("\n");

                     }

                     BFS(graph, visited, i, Q);

              }

       }

}

对所有违背访问过的结点进行广度优先遍历。

1. 获取最短路径，采用迪杰斯特拉算法

void DJ(Graph* graph, int dist[],int distance[], int path[], int v) {//迪杰斯特拉算法,v为起点索引

       int set[MAX];//=1为已找到最短路径，=0为未找到

       int i, j, u, min;

       int cost;

       for ( i = 0; i < graph->vexNum; i++) {

              set[i] = 0;

              path[i] = -1;

              dist[i] = 9999;

              distance[i] = 9999;

       }

       EBox* p = graph->AdjList[v].firstEdge->nextEdge;

       while (p) {

              dist[p->toVex] = p->cost;

              distance[p->toVex] = p->distance;

              path[p->toVex] = v;

              p = p->nextEdge;

       }

       path[v] = -1;

       set[v] = 1;

       dist[v] = 0;

       distance[v] = 0;

       for (i = 0; i < graph->vexNum; i++) {

              min = 9999;

              for (j = 0; j < graph->vexNum; j++) {

                     if (set[j] == 0 && dist[j] < min) {

                            min = dist[j];

                            u = j;

                     }

              }

              set[u] = 1;

              for (j = 0; j < graph->vexNum; j++) {

                     int cost = getCost(graph, u, j);

                     if (set[j] == 0 && dist[u] + cost < dist[j]) {

                            dist[j] = dist[u] + cost;

                            distance[j] = getDistance(graph, u, j) + distance[u];

                            path[j] = u;

                     }

              }

       }

}

1.初始化。V为G中所有顶点集合，path={v}。dist[x]表示从源点到x的已知路径的权值，初始dist[v]为0，其余为无穷大。

2.从源点v开始运行一步广度优先算法即找其相邻点。

3.计算可见点到源点v的路径长度，更新dist[x]。然后对路径进行排序，选择最短的一条作为确定找到的最短路径，将其终点加入到path中.

4.从path中选择新加入的点运行广度优先算法找其相邻点，重复step3。直至所有点已加入S或者再搜索不到新的可见点（图中存在不联通的点，此时path<V）终止算法。

void printPath(Graph* graph,int path[], int v1) {//v1为终点索引,从终点往前打印路径

       if (path[v1] == -1) {

              printf("%s", graph->AdjList[v1].name);

       }

       else {

              printPath(graph,path, path[v1]);//v1变为v1的前驱

              printf("--->%s", graph->AdjList[v1].name);

       }

}

打印从起点v到终点v1的路径

void shortestRoute(Graph* graph) {

       char start[30];

       char end[30];

       int dist[MAX], path[MAX], distance[MAX];//dist存储每条最短路径的花费总和，path[i]存储索引为i的城市的的前驱结点索引，distance存储每条最短路径的路程总和

       printf("\n请输入起点和终点（用空格隔开）:\n");

       scanf("%s %s", start,end);

       int v0 = getLocation(graph, start);

       int v = getLocation(graph, end);

       if (v0 != -1 && v != -1) {

              DJ(graph, dist, distance, path, v0);

              if (dist[v] != 9999) {

                     printf("\n%s到%s费用最少的路线：\n", start, end);

                     printf("花费%d，距离为%d公里\n", dist[v], distance[v]);

                     printf("\n路线为：\n");

                     printPath(graph, path, v);

                     printf("\n");

              }

              else {

                     printf("\n%s到%s不连通，所以无最短路径\n", start, end);

              }

       }

       else {

              printf("\n未找到此城市！\n");

       }

}

输入起始点，并输出其最短路径权值总和和最短路径。

遍历运行结果：

测试用例

编号	输入	预计输出	实际输出	实验结果评估
1	London Lisbon	花费245，距离为3000公里 London-->Paris-->Bern-->Madrid -->Lisbon		结果符合预期
2	London London	花费0，距离为0公里 London		符合预期
3	Lisbon Bucharest	花费165，距离4550公里 Lisbon-->Madrid-->Bern-->Sarajevo-->Budapest-->Bucharest		符合预期
4	Lisbon Belfast	不连通，无最短路径		符合预期

实验结果总结

对每个实验分别进行测试总结

实验一：

链表不要求在创建时就确定链表长度，所以适合在不确定数据地数量时使用，但是链表不能根据索引直接找到某个结点，而要从头开始找，因此链表的插入和删除效率比较低，当数据量比较大而且要频繁地查找和删除数据时不推荐使用。

实验二：

用栈来进行表达式求值的难点在于判断操作符的优先级，在该实验中，设置一个操作符数组，用于获取运算符优先级。

/* 存储运算符和界限符 */

       char OP[7] = { '+', '-', '*', '/', '(', ')', '#' };

       /* OP的优先级表 */

       char pre[][7] = {

                                   {'>', '>', '<', '<', '<', '>', '>'},

                                   {'>', '>', '<', '<', '<', '>', '>'},

                                   {'>', '>', '>', '>', '<', '>', '>'},

                                   {'>', '>', '>', '>', '<', '>', '>'},

                                   {'<', '<', '<', '<', '<', '=', '0'},

                                   {'>', '>', '>', '>', '0', '>', '>'},

                                   {'<', '<', '<', '<', '<', '0', '='}

       };

	+	-	*	/	（	）	#
+	>	>	<	<	<	>	>
-	>	>	<	<	<	>	>
*	>	>	>	>	<	>	>
/	>	>	>	>	<	>	>
（	<	<	<	<	<	=
）	>	>	>	>		>	>
#	<	<	<	<	<		=

如下图所示：

a为当前读取的操作符，b为当前操作符栈顶元素：

1. a>b 　a的优先权高于ｂ,a不入栈，操作数出栈与a后面的操作数作a运算，结果入操作数栈；
2. a<b　  a的优先权低于ｂ，a入栈；
3. a=b　　a的优先权等于ｂ

加减乘除优先性都低于“（”，但是高于“）”，为了算法简洁，在表达式的左边和右边虚设一个“#”，这一对“#”表示一个表达式求值完成“（”=“）”表示当一对括号相遇时表示括号内已运算完成。“）”和“（”、“#”和“(”、“(”和“#”无法相继出现如果出现则表达式出现语法错误。 

栈在表达式求值中有较为广泛的运用。

实验三：

本实验需要从文件中读取数据来构建树，还有从文件中读取问题并提取出关键字来在树中寻找相应的结果，本实验让我对树的构建和基本操作以及文件读取，字符串操作都得到了更深的理解。

实验四：

本实验实现了图的创建，遍历和求最短路径的操作，其中最短路径问题为该实验的重难点，在本实验中，我使用了迪杰斯特拉算法，本算法思路比较简单，在不使用堆优化的情况下，时间复杂度为O(E2),使用二叉堆后能优化到O((V+E)logE),效率还是挺可观的。

通过本实验，我掌握了图的邻接表式创建和遍历，以及常规迪杰斯特拉算法求最短路径。