八皇后问题--＞n皇后问题解法--＞树的遍历应用

问题表述：八皇后问题是一个以国际象棋为背景的问题：如何能够在8×8的国际象棋棋盘上放置八个皇后，使得任何一个皇后都无法直接吃掉其他的皇后？为了达到此目的，任两个皇后都不能处于同一条横行、纵行或斜线上。八皇后问题可以推广为更一般的n皇后摆放问题：这时棋盘的大小变为n×n，而皇后个数也变成n。当且仅当n = 1或n ≥ 4时问题有解。

 为了研究八皇后问题 我们先研究一个最简单的n=4的时候的四皇后问题  

下面为四皇后问题图解：

 由图中可以看出，如果将四皇后问题的推进每一个皇后落点的状态串在一起，可以看出，这其实就是一颗状态树，而四皇后问题的结果也存在于树的叶子结点，所以可以进行深度优先遍历这棵树，在叶子结点中查找四皇后的解，类似也可以得出八皇后问题的解法

下面进行八皇后问题的分析： 

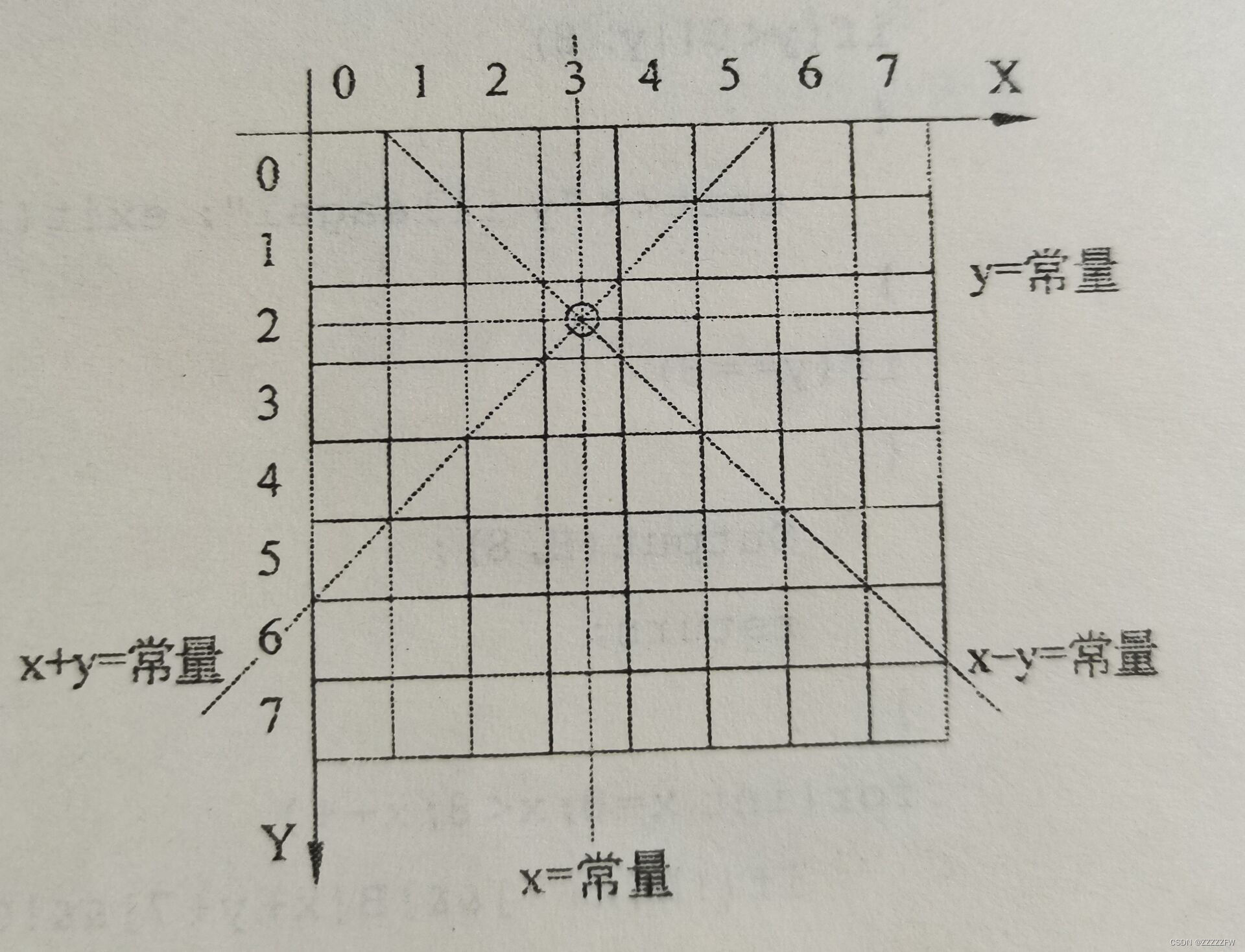
当一个皇后占位为(x,y)时，在其水平方向，垂直方向和两个对角线方向上都不可以在放其余的皇后。如果每行只放一个皇后，则水平方向就不需要考虑了，只需要考虑其他三个方向。

坐标图： 

水平方向的直线方程是“y=常量”，垂直方向的直线是“x=常量”，两个对角线方向的直线方法分别是“x-y=常量”和“x+y=常量”

用三个一维数组A，B，C记录皇后占位(x,y)，称为状态数组。使其初始值为0。表示棋盘上还没有皇后。如果有一个皇后占位(x,y),令A[x]=B[x+y]=C[x-y]=1(不一定非得是1，只是与0不同表示当前位置被皇后占领)。 下一个皇后能否占位(x',y')的前提是A[x']=B[x'+y']=C[x'-y']=0(必须是同时为0)

作为下标数组，x，y的取值为0~7，所以x+y的取值为0~14，x-y的取值为-7~7，由于数组的下标不能为负数，所以我们等价的转换成每个下标都+7，即A[x+7],B[x+y+7],C[x-y+7],这样可以保证数组的下标不出现负数。所以最大的范围为14+7=21，所以ABC三个状态数组开辟空间大小为A[22],B[22],C[22] 

具体实现:深度优先遍历状态树，查找叶子，用长度为8的一维数组H，逐行记录皇后的占位，即H[y]=x;表示皇后占位为(x,y),y从0开始一直到7，当y=8时说明一次深度遍历已经到最底层，得到叶子，也就是八皇后问题的一种解 

八皇后问题代码实现: 

void Queen(int y = 0)
{
    static int A[22], B[22], C[22], H[8]; // 0~21有22个长度 静态数据类型使得递归时能够用的是同一个状态数组
    if (y < 0 || y > 8)
    {
        return;
    } // y错误

    if (y == 8) //递归结束条件
    {
        OutPut(H, 8); //输出解
    }

    for (int x = 0; x < 8; x++)
    {
        if (!A[x + 7] && !B[x + y + 7] && !C[x - y + 7])
        {
            H[y] = x;                                   //皇后占位(x,y)
            A[x + 7] = B[x + y + 7] = C[x - y + 7] = 1; //状态更新表示被占位
            Queen(y + 1);                               //带着当前一行已经有皇后的情况进行下一层的递归
            A[x + 7] = B[x + y + 7] = C[x - y + 7] = 0; //状态回溯 回到上一行的时候状态要重新置为0 表示这一行还没有皇后占位
        }
    }
}

template<class T>
void OutPut(const T* p,int n)
{
    static int total=1;
    for(int y=0;y<n;y++)
    {
        if(y==0)
        {
            cout<<"("<<total++<<")"<<":"<<endl;
        }

        for(int x=0;x<n;x++)
        {
            if(x==p[y]){cout<<"@"<<" ";}
            else{cout<<"#"<<" ";}
        }
        cout<<endl;
    }
    cout<<endl;
    system("pause");
    system("cls");
}

 八皇后问题一次深度得到解的过程示意:

 

处理完八皇后问题，n皇后问题也不在话下了，记住n>=4

n皇后问题分析:

n皇后问题解法:

void Queen(int* A,int* B,int* C,int* H,int n,int y=0)//A,B,C,H与八皇后问题性质一样 n表示n*n的棋盘
{
    if(y<0||y>n){return;}

    if(y==n)//递归返回条件
    {
        OutPut(H,n);
        return;
    }

    for(int x=0;x<n;x++)
    {
        if(!A[x+n-1]&&!B[x+y+n-1]&&!C[x-y+n-1])
        {
            H[y]=x;//表示皇后在(x,y)
            A[x+n-1]=B[x+y+n-1]=C[x-y+n-1]=1;//状态更新
            Queen(A,B,C,H,n,y+1);
            A[x+n-1]=B[x+y+n-1]=C[x-y+n-1]=0;//状态返回
        }
    }
}

main函数内容:(包括运行结果截图)

#include<bits/stdc++.h>
using namespace std;

//n皇后问题的求解

template<class T>
void OutPut(const T* p,int n)
{
    static int total=1;
    for(int y=0;y<n;y++)
    {
        if(y==0)
        {
            cout<<"("<<total++<<")"<<":"<<endl;
        }

        for(int x=0;x<n;x++)
        {
            if(x==p[y]){cout<<"@"<<" ";}
            else{cout<<"#"<<" ";}
        }
        cout<<endl;
    }
    cout<<endl;
    system("pause");
    system("cls");
}

void Queen(int* A,int* B,int* C,int* H,int n,int y=0)//A,B,C,H与八皇后问题性质一样 n表示n*n的棋盘
{
    if(y<0||y>n){return;}

    if(y==n)//递归返回条件
    {
        OutPut(H,n);
        return;
    }

    for(int x=0;x<n;x++)
    {
        if(!A[x+n-1]&&!B[x+y+n-1]&&!C[x-y+n-1])
        {
            H[y]=x;//表示皇后在(x,y)
            A[x+n-1]=B[x+y+n-1]=C[x-y+n-1]=1;//状态更新
            Queen(A,B,C,H,n,y+1);
            A[x+n-1]=B[x+y+n-1]=C[x-y+n-1]=0;//状态返回
        }
    }
}

int main()
{
    int n;
    cout<<"请输入n的值:"<<endl;
    cin>>n;

    int *A=(int*)calloc(3*n-2,sizeof(int));//使用calloc函数可以使A,B,C,D,H所有值都为0
    int *B=(int*)calloc(3*n-2,sizeof(int));
    int *C=(int*)calloc(3*n-2,sizeof(int));
    int *H=(int*)calloc(n,sizeof(int));

    cout<<n<<"皇后问题的解集为:"<<endl;
    Queen(A,B,C,H,n);
    
    system("pause");
    retrun 0;
}

 

(五皇后问题有十种解法)