卡尔曼滤波原理及代码

Acewh

已于 2023-05-01 19:41:41 修改

阅读量2.3k

点赞数 7

文章标签：算法人工智能计算机视觉卡尔曼滤波

于 2023-04-25 18:35:12 首次发布

本文链接：https://blog.csdn.net/m0_63462829/article/details/130351695

版权

一.简介

卡尔曼滤波（Kalman filtering）是一种利用线性系统状态方程，通过系统输入输出观测数据，对系统状态进行最优估计的算法，它可以在任意含有不确定信息的动态系统中使用，用来对目标的位置进行预测，并且利用预测结果对跟踪的目标进行修正，属于自动控制理论中的一种方法。它很适合持续变化的系统，并且占用内存少，非常适合实时问题与嵌入系统，在单目标还是多目标领域都是很常用的一种算法。

例如一个无人驾驶汽车想要在城市中自由行驶，它必须知道自己的确切位置才能进行导航。关于如何导航，我们一般有以下方式：

GPS装置，但缺点是精度可能太低；
里程表、惯性测量等传感器得出的信息；
汽车发动机温度、邮箱液体量信息；
汽车运动程序本身发出的指令等。

以上信息存在精度误差，并且实际行驶情况可能存在自然与非自然因素影响，所以得出的导航结果不是非常准确。

卡尔曼滤波的作用就是综合利用以上信息，根据其本身噪声，分配一定权重，去估计获得一个导航信息的最优估计。

二.原理

不同的场景有不同的预测函数，比如在汽车行驶场景中，汽车的初始速度、位置、加速度等信息，结合速度、位置的计算公式可以预测出汽车下一时刻速度、位置状态信息，我们称之为原始预测结果；汽车的里程表、GPS等设备的传感器也会给我们汽车下一时刻速度、位置的状态信息，我们称之为观测结果；根据观测结果对原始预测结果进行修正，得到的结果称为预测结果（也称先验估计）。

在实际情况中，预测结果和观测结果都有一定的误差，给出的信息都不一定准确，而卡尔曼滤波会将两者融合，充分利用已有信息得出更加准确的结果，得出的结果称为后验估计。

1.先验估计原理

现在只考虑汽车有两个状态变量信息，在某一时刻它的速度是v，位置是p，用一个向量表示为：

$\vec{x}=\begin{bmatrix} p\\ v \end{bmatrix}$

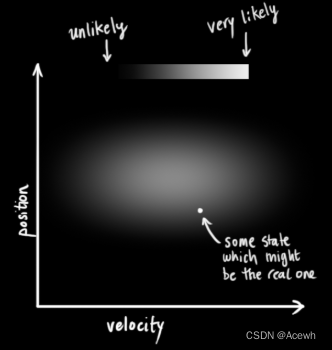
如图1所示，实际上我们并不能获得汽车准确的速度velocity与位置position，它们之间会有很多组合，卡尔曼滤波算法认为它们都服从一个高斯分布，每个变量都有一个均值μ与方差 $\sigma ^2$ 。图1中越暗表示变量值的概率越低，越亮表示值的概率越高，高斯分布的中心表示p与v的各自的最优估计（即均值μ），用 $\hat{x}$ 表示。

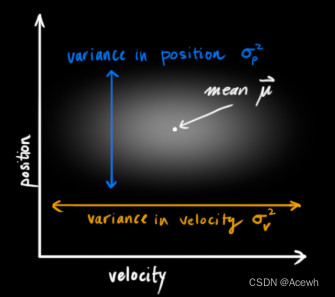
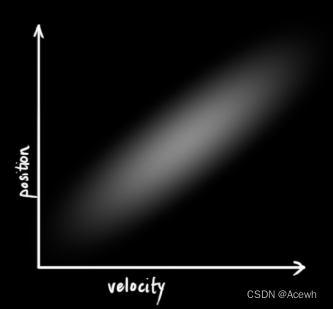
如图2所示，表示位置与速度这两个变量不相关，意味着不能由一个变量推出另一个变量的值。如图3所示，表示位置与速度这两个变量相关，意味可以由一个变量推出另一个变量的值。变量间的相关性用协方差矩阵表示，矩阵中每个元素 $\sum_{ij}$ 表示第i个和第j个状态变量之间的相关度。


图1 高斯分布变量	图2 不相关变量	图3 相关变量

（1）当前时刻的状态

在只考虑汽车p与v两个变量时，在时刻 k 的状态(p与v最佳估计)与协方差矩阵可表示为：

$\hat{x}_{k}=\begin{bmatrix} p\\ v \end{bmatrix},P_{k}=\begin{bmatrix} \sum_{pp}& \sum_{pv}\\ \sum_{vp} & \sum_{vv} \end{bmatrix}$

（2）预测下一时刻状态

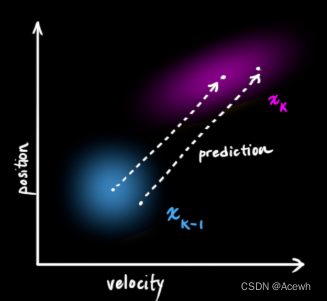
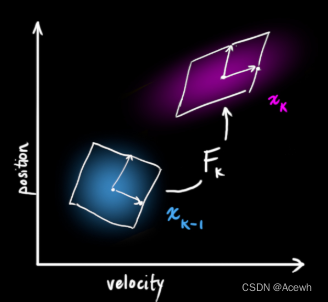
如图4所示，根据汽车当前时刻(k-1)的状态，来预测下一时刻(k)的状态，预测函数并不在乎所有预测结果中哪些相对准确，哪些不准确，它会对所有的可能性预测，给出一个新的高斯分布。


图4 前后时刻变量的高斯分布	图5 前后时刻的状态转移

如图5所示，预测函数需要某种规律将汽车从 k-1 时刻的状态变为 k 时刻的状态，而这个规律被称为状态转移矩阵 $F_{k}$ 。汽车在做匀速运动时，其位置与速度的变化关系为：

$\begin{cases} p_{k}=p_{k-1}+\Delta t\quad v_{k-1}\\ v_{k}=v_{k-1} \end{cases}$

所以下一时刻的状态用矩阵形式表示为：

$\hat{x}_{k}=\begin{bmatrix} 1 & \Delta t\\ 0 & 1 \end{bmatrix}\hat{x}_{k-1}=F_{k}\hat{x}_{k-1}$

根据协方差性质，下一时刻的协方差矩阵为：

$P_{k}=F_{k}P_{k-1}F_{k}^{T}$

（3）外部控制

汽车在运动过程中并不总是匀速运动，假设汽车某个时刻的加速度是a，那么下一时刻位置与速度的变化关系为：

$\left\{\begin{matrix} p_{k}=p_{k-1}+\Delta t v_{k-1}+\frac{1}{2}a\Delta t^2 \\ v_{k}=v_{k-1}+a\Delta t \quad\quad\quad\quad\quad \end{matrix}\right.$

所以下一时刻的状态用矩阵形式表示为：

$\hat{x}_{k}=F_{k}\hat{x}_{k-1}+\begin{bmatrix} \frac{\Delta t^2}{2} \\ \Delta t \end{bmatrix}a=F_{k}\hat{x}_{k-1}+B_{k}u_{k}$

$F_{k}$ 为状态转移矩阵； $B_{k}$ 为状态控制矩阵，表明对小车如何加速减速； $u_{k}$ 为状态控制向量，表明控制的力度大小和方向。

（4）外部影响

汽车在行驶过程中不免受到风速、路况等外部不确定因素的影响，假设这些因素同样服从高斯正态分布 $w_{k}\sim N(0, Q_{k})$ ，则汽车下一时刻状态完整预测公式为：

$\hat{x}_{k}=F_{k}\hat{x}_{k-1}+B_{k}u_{k}+w_{k}$ （1）

$P_{k}=F_{k}P_{k-1}F_{k}^{T}+Q_{k}$ （2）

一般情况下假设 $w_{k}$ =0即可，明确不为0时再根据实际情况设置。

（5）根据原始观测结果修正预测结果

汽车当前状态的原始预测结果与传感器给出的观测结果虽然都有一定的误差，但它们都多多少少给出了汽车当前时刻的信息，两者之间具备某种特定关系，如图6所示，左边为原始预测结果的高斯分布，右边为观测结果的高斯分布，它们的特定关系用矩阵 $H_{k}$ 表示。

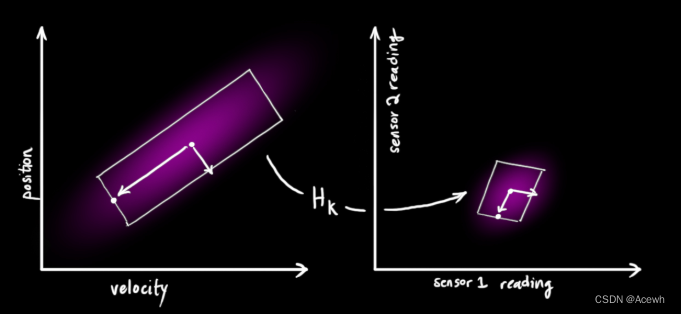
最后得出的预测结果为：

$\mu =H_{k}\hat{x}_{k}$

$\sum =H_{k}P_{k}H_{k}^T$

2.后验估计原理

（1）观测结果和实际结果的关系

实际中，汽车下一时刻真实的状态称为实际结果，传感器给出的观测结果与实际结果间同样存在不确定性，它同样服从一个高斯分布 $z_{k}\sim N(0, R_{k})$ 。

（2）最优估计

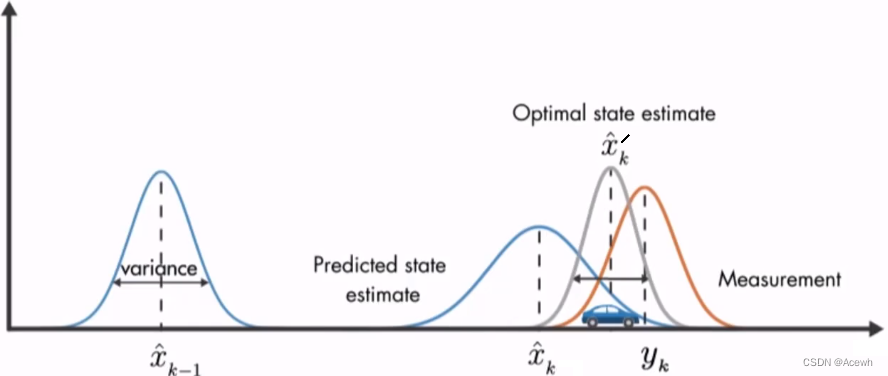
如图7所示，

蓝色 $\hat{x}_{k}$ 表示当前时刻的预测结果： $(\mu_{0},\sum _0)=(H_{k}\hat{x}_{k}, H_{k}P_{k}H_{k}^{T})$
橙色 $y_{k}$ 表示当前时刻的观测结果： $(\mu_{1},\sum_{1})=(z_{k},R_{k})$
它们之间的灰色 $\hat{x}_{k}^{'}$ 便是实际结果的最优估计。

根据高斯分布融合公式： $\left\{\begin{matrix} K=\sum_{0}(\sum_{0}+\sum_{1})^{-1}\\ \mu=\mu_{0}+K(\mu_{1}-\mu_{0})\\ \sum^{'}=\sum_{0}-K\sum_{0} \end{matrix}\right.$ ，可得出最优估计 $\hat{x}_{k}^{'}$ 的计算公式为：

$K=H_{k}P_{k}H_{k}^{T}(H_{k}P_{k}H_{k}^{T}+R_{k})^{-1}$ （4）

$H_{k}\hat{x}_{k}^{'}=H_{k}\hat{x}_{k}+K(z_{k}-H_{k}\hat{x}_{k})$ （5）

$H_{k}P_{k}^{'}H_{k}^{T}=H_{k}P_{k}H_{k}^{T}-KH_{k}P_{k}H_{k}^{T}$ （6）

公式 (4) (5) (6) 左乘 $H_{k}^{-1}$ ，公式 (6) 右乘 $H_{k}^{T-1}$ 得：

$K^{'}=P_{k}H_{k}^{T}(H_{k}P_{k}H_{k}^{T}+R_{k})^{-1}$ （7）

$\hat{x}_{k}^{'}=\hat{x}_{k}+K^{'}(z_{k}-H_{k}\hat{x}_{k})$ （8）

$P_{k}^{'}=P_{k}-K^{'}H_{k}P_{k}$ （9）

3.总结

根据1和2的内容，简化公式 (1) (2) (7) (8) (9) 得出卡尔曼滤波最终的计算公式为：

预测：

$x=F*x+B*u$

$P=F*P*F^{T}+Q$

更新：

$K=P*H^{T}*(H*P*H^{T}+R)^{-1}$

$x=x+K*(z-H*x)$

$P=(I-K*H)*P$

x	系统状态	F	状态转移矩阵
B	状态控制矩阵	u	状态控制向量
P	变量协方差矩阵	Q	噪声对原始预测结果造成的协方差矩阵
K	卡尔曼增益	H	原始预测结果与观测结果的关系矩阵
z	观测结果	R	噪声对观测结果造成的协方差矩阵

注意：

实际中可以不断调整Q和R来得出最好的效果。

上述更新步骤中最后一步矩阵P形式一般出现在文献中，实际中采用更稳定的计算方式 $P=(I-K*H)*P*(I-KH)^T+K*R*K^T$

三.示例

1.手动计算方式

import numpy as np
import matplotlib.pyplot as plt
plt.rcParams['font.sans-serif'] = ['SimHei']


# 时间设置
delta_t = 0.1                           # 每秒钟采一次样
end_t = 8                               # 时间长度
time_t = end_t * 10                     # 采样次数
t = np.arange(0, end_t, delta_t)        # 设置时间数组

# 卡尔曼滤波矩阵设置
X = np.mat([[0], [0]])                  # 系统初始状态
P = np.mat([[1, 0], [0, 1]])            # 状态协方差矩阵

A = np.mat([[1, delta_t], [0, 1]])      # 状态转移矩阵
B = [[1 / 2 * (delta_t ** 2)], [delta_t]]  # 状态控制矩阵
u = 1                                   # 状态控制向量
H = np.mat([1, 0])                      # 原始预测结果与观测结果关系矩阵（观测矩阵）


# 真实结果
x = 1 / 2 * u * t ** 2

# 测量结果
v_var = 1                               # 测量噪声的方差
v_noise = np.round(np.random.normal(0, v_var, time_t), 2)
v = np.mat(v_noise)                     # 定义测量噪声
z = x + v                               # 定义测量结果
X_mat = np.zeros(time_t)                # 初始化记录系统预测优化值的列表


def KF(X,P,Q,R):
    for i in range(time_t):
        # 预测
        X = A * X + np.dot(B, u)        # 估算状态变量
        P = A * P * A.T + Q             # 估算状态误差协方差
        # 更新
        K = P * H.T / (H * P * H.T + R) # 更新卡尔曼增益
        X = X + K * (z[0, i] - H * X)   # 更新预测优化值
        P = (np.eye(2) - K * H) * P     # 更新状态误差协方差
        # 记录系统的预测优化值
        X_mat[i] = X[0, 0]              # 第一个状态：位置

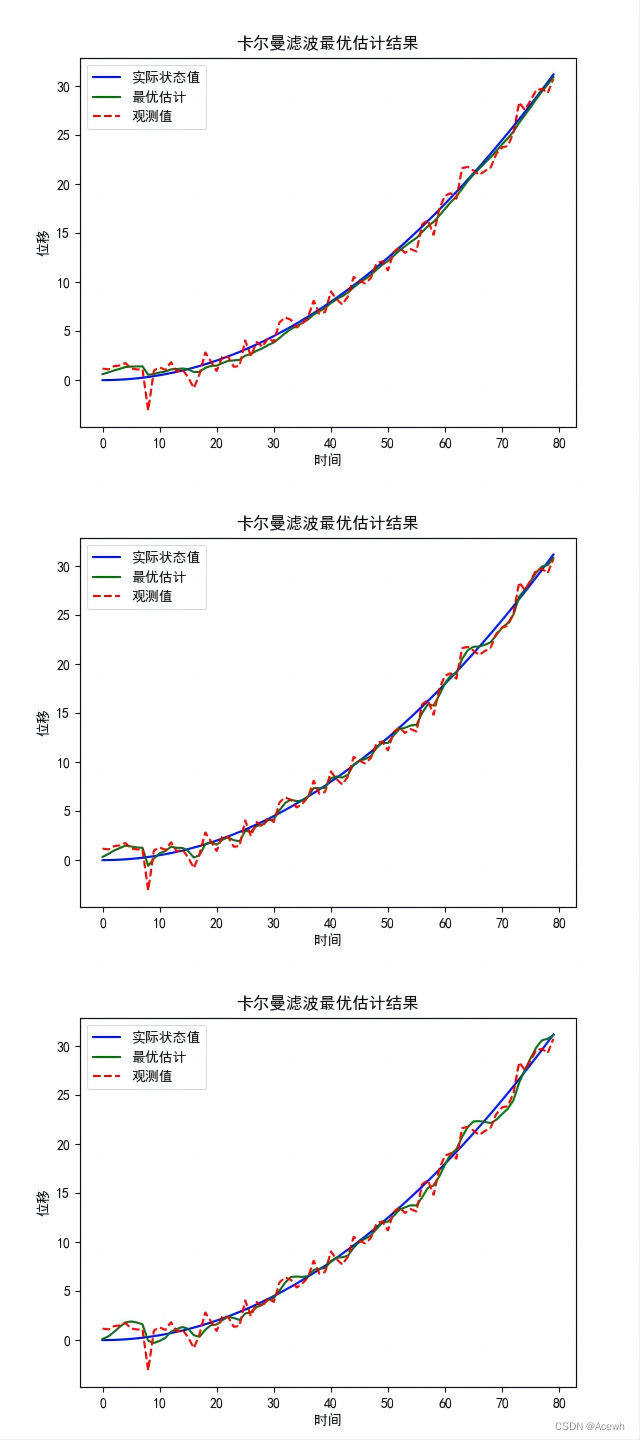
    plt.plot(x, "b", label='实际状态值')  # 设置曲线数值
    plt.plot(X_mat, "g", label='最优估计')
    plt.plot(z.T, "r--", label='观测值')
    plt.xlabel("时间")
    plt.ylabel("位移")
    plt.title("卡尔曼滤波最优估计结果")
    plt.legend()
    plt.show()




if __name__ == '__main__':
    Q1 = np.mat([[0.001, 0], [0, 0.001]])  # 预测噪声 协方差矩阵
    R1 = np.mat([1])                       # 观测噪声 协方差矩阵

    Q2 = np.mat([[10.001, 0], [0.5, 0.001]])
    R2 = np.mat([30])

    Q3 = np.mat([[0.001, 0.05], [10, 0.001]])
    R3 = np.mat([10])

    # 不同QR的KF结果
    KF(X,P,Q1,R1)
    KF(X,P,Q2,R2)
    KF(X,P,Q3,R3)

2.API计算

import numpy as np
import matplotlib.pyplot as plt
from filterpy.kalman import KalmanFilter
plt.rcParams['font.sans-serif'] = ['SimHei']


# 小车的真实值
delta_t = 0.1                           # 每秒钟采一次样
end_t = 8                               # 时间长度
time_t = end_t * 10                     # 采样次数
t = np.arange(0, end_t, delta_t)        # 设置时间数组
u = 1
z = 1 / 2 * u * t ** 2

# 小车的观测值
noise = np.around(np.random.normal(0,1,time_t),2)
z_noise = z + noise

# 卡尔曼滤波器对象
kfilter = KalmanFilter(dim_x=2,dim_z=1,dim_u=1)
'''
dim_x 表示状态向量个数，[p,v]表示位置和速度，所以为2
dim_z 表示要观测的向量个数，只观测位置p，所以为1
dim_u 表示状态控制向量个数，只有汽车的加速度u，所以为1
'''

def mykf():
    # 系统状态初始值
    kfilter.x = np.mat([[0], [0]])
    # 变量协方差矩阵, 假设位置p与速度v不相关
    kfilter.P = np.mat([[1,0],[0,1]])
    # 状态转移矩阵, 假设匀加速运动
    kfilter.F = np.mat([[1, delta_t], [0, 1]])
    # 状态控制矩阵
    kfilter.B = np.mat([[1 / 2 * (delta_t ** 2)], [delta_t]])
    # 关系矩阵
    kfilter.H = np.mat([1, 0])
    # 预测噪声协方差矩阵
    kfilter.Q = np.mat([[0.001, 0], [0, 0.001]])
    # 观测噪声协方差矩阵
    kfilter.R = np.mat([1])

    # 对位置与速度进行更新
    z_kf_list = [] # 位置估计
    v_kf_list = [] # 速度估计
    for i in range(time_t):
        kfilter.predict(u)   # 预测
        kfilter.update(z_noise[i])    # 更新
        x = kfilter.x
        z_kf_list.append(x[0,0])
        v_kf_list.append(x[1,0])

    plt.plot(z, "b", label='实际状态值')  # 设置曲线数值
    plt.plot(z_kf_list, "g", label='最优估计')
    plt.plot(z_noise.T, "r--", label='观测值')
    plt.xlabel("时间")
    plt.ylabel("位移")
    plt.title("卡尔曼滤波最优估计结果")
    plt.legend()
    plt.show()

if __name__ == '__main__':
    mykf()

Acewh

关注

7
点赞
踩
33

收藏

觉得还不错? 一键收藏
0
评论
卡尔曼滤波原理及代码

卡尔曼滤波（Kalman filtering）是一种利用线性系统状态方程，通过系统输入输出观测数据，对系统状态进行最优估计的算法，它可以在任意含有不确定信息的动态系统中使用，用来对目标的位置进行预测，并且利用预测结果对跟踪的目标进行修正，属于自动控制理论中的一种方法。它很适合持续变化的系统，并且占用内存少，非常适合实时问题与嵌入系统，在单目标还是多目标领域都是很常用的一种算法。例如一个无人驾驶汽车想要在城市中自由行驶，它必须知道自己的确切位置才能进行导航。GPS装置，但缺点是精度可能太低；
复制链接

扫一扫