1.整数线性规划问题:
某公司生产三种产品,分别为A、B和C。生产这些产品需要使用三种资源,分别为R1、R2和R3,其总资源为50、65、80。
已知每种产品的生产量、所需资源量以及每种资源总量,我们需要确定每种产品的最优生产量,使得公司总利润最大。
产品A所需资源R1为2单位/件,产品B所需资源R1为3单位/件,产品C所需资源R1为1单位/件。
产品A所需资源R2为1单位/件,产品B所需资源R2为2单位/件,产品C所需资源R2为3单位/件。
产品A所需资源R3为3单位/件,产品B所需资源R3为1单位/件,产品C所需资源R3为2单位/件。
另外,我们还知道每种产品的单位利润分别为:产品A的单位利润为4000元/件,产品B的单位利润为6000元/件,产品C的单位利润为5000元/件。
现在我们要来解这个线性规划问题,找出使得总利润最大的产品生产量。该规划问题为:

2.lingo求解
lingo:点击solve(解决)

结果:

注意在生产产品时生产量应该是整数,因此限制变量为整数。所以需要修改代码为:
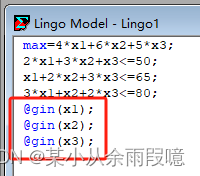
得到最终结果:

这样写更规范:


2.敏感性分析
在线性规划中,参数价值(对偶价值)和资源向量(右端向量)是通过对线性规划模型的系数和约束条件进行扰动来进行灵敏度分析的重要概念。这种分析有助于了解模型解的稳健性,即在输入数据发生变化时,最优解的变化程度。
点击lingo( /soler) ->option -> general solver -> Dura Computations -> Price& ranges ->apply -> save-> ok
再点击lingo( /soler) ->Range
结果报错:

这是因为不允许对整数编程模型进行范围分析。
重新分析:
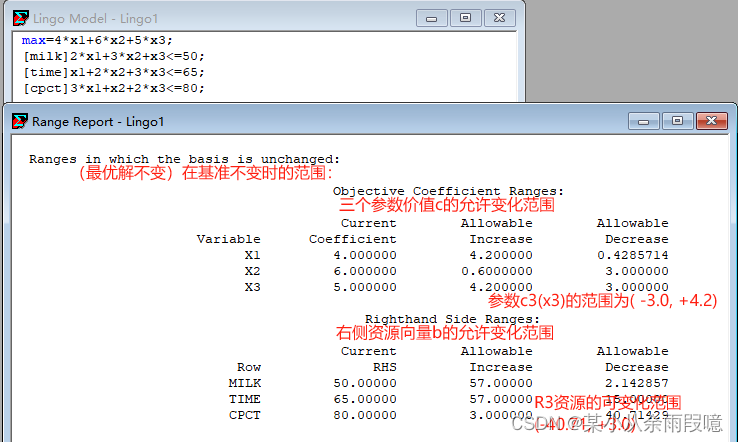







 本文讨论了一家公司的整数线性规划问题,目标是确定A、B、C三种产品的最优生产量以最大化利润。使用LINGO求解并考虑了生产量为整数的限制。同时,文章介绍了敏感性分析的概念,探讨了参数变化对最优解的影响,但在整数编程模型中无法进行范围分析。
本文讨论了一家公司的整数线性规划问题,目标是确定A、B、C三种产品的最优生产量以最大化利润。使用LINGO求解并考虑了生产量为整数的限制。同时,文章介绍了敏感性分析的概念,探讨了参数变化对最优解的影响,但在整数编程模型中无法进行范围分析。
















 1万+
1万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








