信息论中自信息量与平均信息量的计算及其最大信息量与概率的关系

 信息论是运用概率论与数理统计的方法研究信息、信息熵、通信系统、数据传输、密码学、数据压缩等问题的应用数学学科。信息系统就是广义的通信系统，泛指某种信息从一处传送到另一处所需的全部设备所构成的系统。

信息论将信息的传递作为一种统计现象来考虑，给出了估算通信信道容量的方法。信息传输和信息压缩是信息论研究中的两大领域。这两个方面又由信息传输定理、信源－信道隔离定理相互联系。

在本篇文章里主要解决的是自信息量和离散信源平均信息量的计算及讨论二元离散信源的最大信息量与概率的关系。

一、自信息量的计算

 对于离散信源而言，信源的概率为P(x)。信源输出一个消息提供的信息量就等于信源的不确定度。当概率P越小，x消息出现的概率就越小，一旦出现所获得的信息量就越大。

当计算自信息量时，可以使用以下公式：

I(x) = -log2(p(x))

其中 p(x) 代表事件 x 的概率，这里使用的底数为2，自信息量的测度单位为比特bite。

让我们来举一个例子，计算一个硬币投掷事件的自信息量。

假设我们有一枚公平的硬币，投掷时正面朝上的概率是 0.5（50%），反面朝上的概率也是 0.5。我们想要计算正面朝上的自信息量。

根据公式：

I(正面) = -log2(0.5)

现在我们计算它：

I(正面) = -log2(0.5) ≈ -(-1) ≈ 1比特

这表示正面朝上的事件提供了1比特的信息。因为这是一个公平的硬币，正反面出现的概率相等，所以它提供了一半的信息。计算的Python代码如下，这里可以选择测度单位和自己输入概率。

# 导入包
import math
# 定义函数：计算自信息量
def calculate_information(probability, a):
    if probability <= 0 or probability >= 1:
        raise ValueError("Probability must be between 0 and 1")
    else:
        if a == '2':
            information = -math.log2(probability)
            print(f"事件的自信息量为: {information} 比特")
        elif a == 'e':
            information = -math.log(probability)
            print(f"事件的自信息量为: {information} 奈特")
        elif a == '3':
            information = -math.log10(probability)
            print(f"事件的自信息量为: {information} 铁特")
        else:
            raise ValueError("Invalid unit choice")
# 输入变量
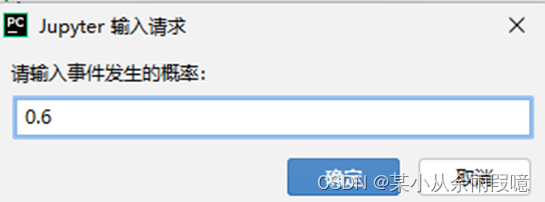
x = float(input("请输入事件发生的概率："))
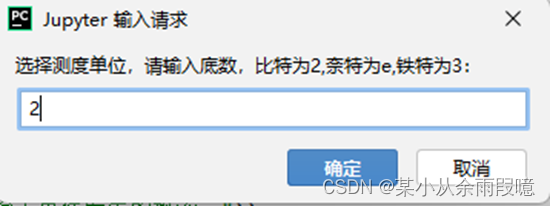
a = str(input("选择测度单位，请输入底数，比特为2,奈特为e,铁特为3："))
# 使用函数
information = calculate_information(x, a)

 通过程序输入事件发生的概率和测度单位后，可以通过使用定义的函数计算出某个事件的自信息量，代码中设置了错误提示。这里要求事件的概率属于[0,1]区间，如下：

二、离散信源平均信息量的计算

此处，通过考虑变量的约束、计算公式等来定义一个名为average_information(probabilities)的函数，调用函数来进行离散信源平均信息量的计算。

import math

def average_information(probabilities):
    # if sum(probabilities.values()) != 1:
    #     raise ValueError("概率之和必须等于1")

# 计算概率之和时，涉及到多个浮点数相加，这些浮点数可能在计算时引入了小的近似误差。这个误差通常很小，但当你要求概率之和严格等于1时，可能会导致问题。
# 使用误差范围来比较概率之和
    epsilon = 1e-10  # 小的误差范围
    if abs(sum(probabilities.values()) - 1) > epsilon:
        raise ValueError("概率之和必须近似等于1")

    avg_info = 0
    for event, probability in probabilities.items():
        if 0 <= probability <= 1:
            if probability > 0:
                avg_info += probability * (-math.log2(probability))
        else:
            raise ValueError("概率必须在[0,1]")

    return avg_info

# 一个包含离散事件和它们的概率的字典
event_probabilities = {
    'A': 0.4,
    'B': 0.2,
    'C': 0.2,
    'D': 0.2
}

avg_info = average_information(event_probabilities)
print(f"离散信源的平均信息量为: {avg_info} 比特")

在代码中定义了有权值的字典来储存事件的发生概率。这里的约束条件为概率之和需要等于1，并且每个事件的概率必须在区间[0,1]，否则会报错提醒。通过调用定义的函数来计算出离散信源的平均信息量，如下： 

三、二元离散信源的最大信息量与概率的关系

二元离散信源指的是一个信源，它有两个可能的符号或事件，通常用 0 和 1 表示。这两个事件的概率分别为 p(0) 和 p(1)，其中 p(0) + p(1) = 1。

最大信息量表示一个事件所提供的信息的上限，通常以 1 比特为单位。在二元离散信源中，最大信息量与概率 p(0) 和 p(1) 的关系可以通过香农信息理论中的信息熵来解释。

信息熵 H(X) 表示一个随机变量 X 的不确定性，计算公式为：

H(X) = -Σ p(x) * log2(p(x))

其中 p(x) 代表 X 的每个可能事件 x 的概率。对于一个二元离散信源，有两个事件，可以表示为 0 和 1，所以信息熵可以计算为：

H(X) = - p(0) * log2(p(0)) + p(1) * log2(p(1))

最大信息量可以被定义为一个事件提供的最大信息，即提供最大信息熵的事件。在二元离散信源中，当一个事件的概率为 0.5（ p(0) = 0.5，p(1) = 0.5）时，信息熵达到最大值。这是因为在这种情况下，两个事件提供了相等的不确定性，信息熵最大。

总结来说，对于二元离散信源，最大信息量为 1 比特，当两个事件的概率相等时，信息熵最大。如果一个事件的概率接近于 1，那么它提供的信息量接近于 0，因为它是一个非常常见的事件，提供的信息很少。如果两个事件的概率都接近于 0.5，那么它们提供的信息量接近于最大值，因为它们提供了最大的不确定性。