目录
本文的主要公式百度网盘 请输入提取码
提取码:qdwg
第一节——整除性和带余除法
整除性
设a,b,c均为整数,若在某个c使得a=cb成立,则称非零数b整除a。换言之,若b除a没有余数,则认为b整除a。b除a通常用b|a来表示。同时,若b|a,我们说b是a的一个因子。
接下来需要用一些简单的整数整除的性质,如下所示:
- 若a|1,则a=±1。
- 若a|b且b|a,则a=±b。
- 任何不等于零的整数除0。
- 若a|b且b|c,则a|c。
- 对于任意整数m、n,若b|g且b|h,则可得出b|(mg+nh)
最后一条结论的推论为
![]()
![]()
所以
![]()
得出b整除mg+nh。
带余除法
对给定的任意一个正整数n和任意非负整数a,若用n除a,得到整数商q和整数余数r,则满足以下关系式:
![]()
这个式子中![]() 表示小于等于a|n的最大整数。
表示小于等于a|n的最大整数。
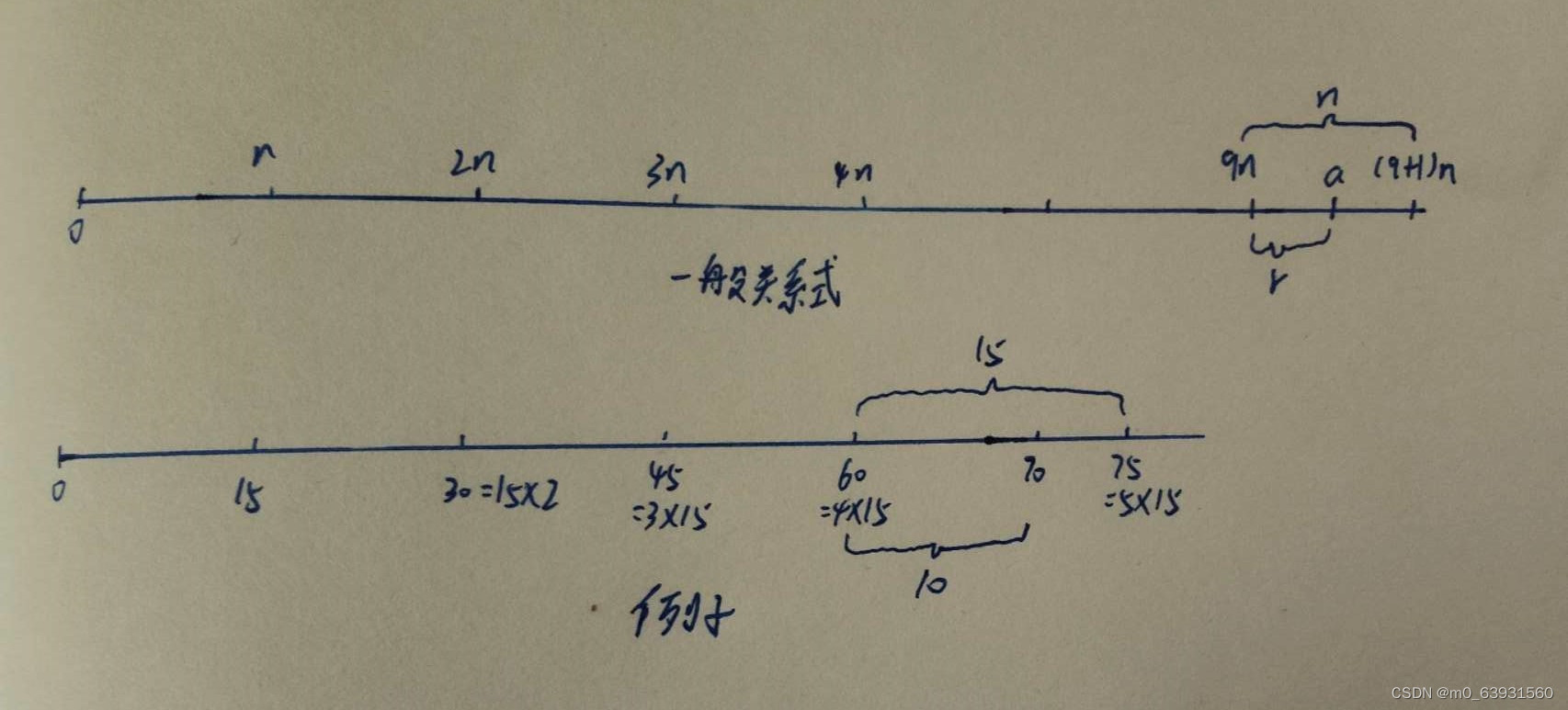
一般关系式表明,对于给定的任意a和正数n,总可以找到满足上述关系的q和r。在数轴上表示整数时,a一定会落在轴上的某处(正数a的情如图所示,类似地,a也可以为负数)。从0开始,依次为n、2n,直到qn,使得qn<=a且(q+1)n>a,其中qn到a的距离为r。这样就得到了唯一的q和r。余数r通常称为剩余数。
第二节——欧几里得算法
欧几里得算法是数论中的一个最基本的技巧,它可以简单的求出两个正整数的最大公因子,首先要一个简单的定义:两个整数是互素的,当且仅当它们只有一个正整数公因子1。
最大公因子
前面讲过,对于整数a,b,m若满足a=mb,则称非零整数b是a的一个因子。我们用gcd(a,b)来表示a的最大公因数,a和b的最大公因子是能同时整除a和b的最大整数。
另外,定义gcd(0,0)=0。更正式的描述是,正整数c称为a和b的最大公因子,如果
- c是a和b的因子。
- a、b的因子都是c的一个因子。
另一个等效的定义如下:
![]()
因为要求最大公因子必须是正数,所以有
![]()
一般来说
![]()
示例
![]()
同样,因为零可以被所有非零整数整除,所以有![]()
如果整数a、b互素,当且仅当它们只有一个正整数公因子1。也就是说,若gcd(a,b)=1,则a,b互质。
求最大公因子
现在来简单描述一个欧几里得算法,它可以简单地求出两个整数的最大公因子。它可以阐述为以下几点:
- 假设我们需要求出整数a和b的最大公因子d;因为gcd(|a|,|b|)=gcd(a,b),所以这里可以假定a>=b>0。
- 使用带余除法,b除a可以表示为
![]()
- 首先考虑到 r=0的情况。由此可知b整除a,且a和b的公因子中不存在比b更大的数。所以有d=gcd(a,b)=b。
- 另外一种情况是r不等于0。在这种情况下,可知一定有d|r。因为由因子的基本性质可知:存在d|a和d|b,那么一定有d|(a-qb),即d|r。
- 在应用欧几里得算法之前,需要知道:gcd(b,r)的值是什么?我们知道d|b和d|r。那么对于任意一个b和r的公因子c,有c|(qh+r)=a。另外,因为c整除a和b,所以一定有c<=d,其中d是a和b的最大公因子,因此有d=gcd(b,r)。
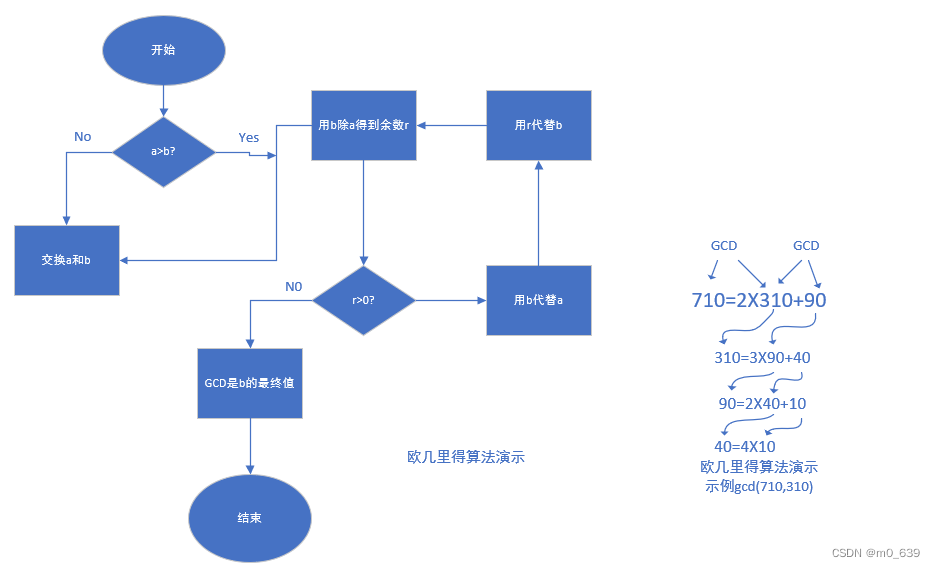
现在我们假设,r不等于0,因为d>r,可以用r除b,然后用带余除法得d=qr+r1 0<=r1<r
如上,若r1=0,则d=r,若r1不等于0,则d=gcd(r,r1)。可以注意到,在计算的过程中,余数会形成递减的一系列非负值,并且余数为零时,算法一定会终止。

每次迭代都进行一次运算,直到
![]()
因此我们可以通过重复运用带余除法来找到两个整数的最大公因子,这个算法称为欧几里得算法。
本质上我们已经能够自顶到下地证明最终结果就是gcd(a,b),我们也可以自底向上的证明。从自底向上的第一步可以看出,

现在可以通过一些较大的数字来看看这个算法的强大之处。
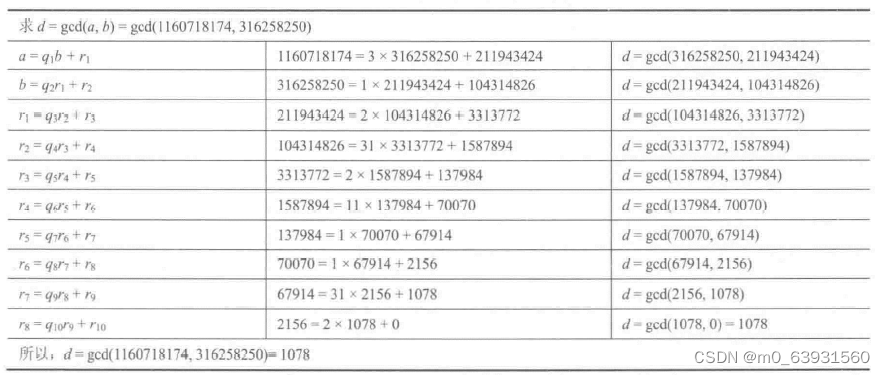
在这个例子中,我们用31625850除1160718174作为开始,得到商为3,余数为2119424,接下来我们用21943424除316258250。继续这个过程,直到余数为零时停止,最终得到的结果1078。将上述计算,过程重新排列为表格的形式,就比较明了。

第三节——模运算
模
如果a是一个整数,n是正整数,则我们定义a除以n所得的余数为a模n。整数n称为模数。因此,对于任意整数a我们总可以把是写成如下形式。
a=qn+r 0≤r<n; q=an
a=(a|n)+(a mod n)
11 mod 7=4; -11 mod 7=3

73=4(mod 23) 21=-9(mod 10)
同时需要注意,如果a=0(mod n),那么n|a。
同余的性质
同余有如下性质:
- 若n|(a-b),则a=b(mod n)
- 若a=b(mod n),则有b=a(mod n)
- 若a=b(mod n),b=c(mod n) ,则有a=c(mod n)
先证明第一条。若n|(a-b),则存在某个k使得(a-b)=kn。于是可知a=b+kn,因此(a mod n)=(b+kn除以n的余数)=(b除以n的余数)=(b mod n)。
23=8(mod 5) 因为 23-8=15=5x3
-11=5(mod 8) 因为 -11-5=-16=8x(-2)
81=0(mod 27) 因为 81-0=81=27x3
剩下的两个性质同样可以很容易的证明。
模算术运算
运算符(mod n)将所有整数映射到集合{0,1,....(n-1}中。于是出现了这样一个问题,能否限制在这个集合上进行算术运算?答案是可以,这种技术称为模算术。
模算术有如下性质:
- [(a mod n)+(b mod n)]mod n=(a+b)mod n
- [(a mod n)-(b mod n)]mod n=(a-b)mod n
- [(a mod n)x(b mod n)]mod n=(axb)mod n
下面证明第一个性质。
![]()
![]()
![]()
剩下的性质同样可以简单的证明。
而在这样的方法中幂运算和普通运算一样,可以通过反复的乘法实现。
![]()
![]()
![]()
![]()
![]()
根据下图给出的加法和乘法的例子,观察模8的加法例子,可以发现结果非常简单,并且矩阵有一定的规律。两个矩阵都关于主对角线对称,因为加法和乘法可以相互替换。与普通的加法运算一样,模运算对于每个整数也存在加法的逆元素,或称为负数。在模运算中,整数x的负数y是使得(x+y)mod 8=0成立的值。可以这样求出左边列中整数的加法逆元素;浏览矩阵的对应行,并找出值0;0所在列顶部的整数就是所求的加法逆元素;如(2+6)mod 8=0。同样在乘法表中,整数x的乘法逆元y是使得(x+y)mod 8=1成立的值。下面我们在乘法表中求一个整数的乘法逆元;浏览矩阵中整数所在的行,并寻找值1;1所在列顶部的整数就是所求的乘法逆元素。如(3x3)mod 8=1。需要指出的是,并非所有整数模8都有乘法逆元。
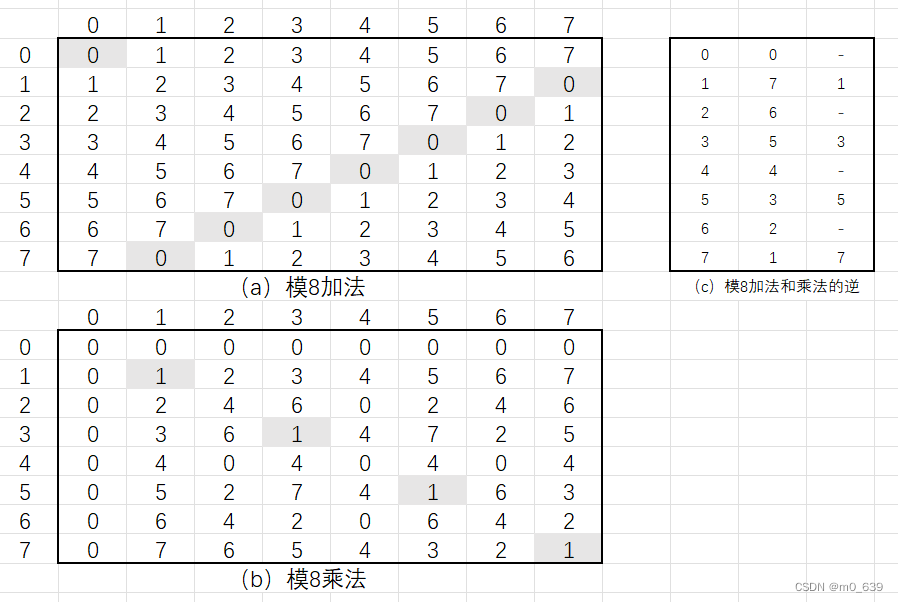
模运算的性质
定义比n小的非负整数集合为![]()
![]()
这个集合称为剩余类集,或模n的剩余类。更准确的说,![]() 中的每个整数都代表一个剩余数,我们可以加模n的剩余数表示为
中的每个整数都代表一个剩余数,我们可以加模n的剩余数表示为![]() ,其中[r]={a:a是一个整数,a=r(mod n)}
,其中[r]={a:a是一个整数,a=r(mod n)}
![]()
![]()
![]()
![]()
在剩余类的所有整数中,我们通常用最小非负整数来代表这个剩余类,寻找与k是模n同余的最小非负整数的过程,称为模n的k约化。
模运算有一个区别于普通运算的特性。首先,如普通算术中的运算一样,有
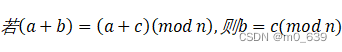
![]()
与加法逆元的存在性是一致的,可得式子
![]()
![]()
其中互素的概念这样定义:如果两个整数的最大公因子是1,则称它们是互素的。也就是说,同乘法逆元的存在性是一致的,于是有
![]()
![]()
通过上面的了解,我们来看加法逆元的存在性不成立的例子。6和8不是互素的,因为它们有公因子2。我们有以下式子:
![]()
![]()
然而,3不等于7(mod 8)。
得到这个奇怪结果的原因是:对于任何一般的模数n,如果a和n有任何公因子的话,用乘数a依次作用与0到n-1的所有整数将不会产生a的一个完整剩余类集。
一般来说,只有当一个整数与n互素时,它才会在![]()
中存在一个乘法逆元。
回顾欧几里得算法
欧几里的算法基于下面的定理,对于任意整数a,b,且![]()
![]()
我们定义d=gcd(a,b),然后,根据gcd的定义,有d|a、d|b成立。对于任何正整数b,可以用整数k,r得到a的一个表示
![]()
![]()
因此,对于某些整数k,存在![]() 由于d|b,所以它也能整除kb。同样我们有d|a,因此可以得到d|(a mod b)。这表示d是b和(a mod b)的公因子。反之,如果d是b和(a mod b)的公因子,那么有d|kb,并且可知
由于d|b,所以它也能整除kb。同样我们有d|a,因此可以得到d|(a mod b)。这表示d是b和(a mod b)的公因子。反之,如果d是b和(a mod b)的公因子,那么有d|kb,并且可知![]() ,即d|a。所以,a和b的公因子的集合等于b和(a mod b)的公因子的集合。因此,两对数(a和b和(a mod b))的gcd相同,定理得证。
,即d|a。所以,a和b的公因子的集合等于b和(a mod b)的公因子的集合。因此,两对数(a和b和(a mod b))的gcd相同,定理得证。
gcd(18,12)=gcd(12,6)=gcd(6,0)=6
gcd(11,10)=gcd(10,1)=gcd(1,0)=1
方案展示如下

可用下面的递归函数更加精确的定义欧几里得算法:
![]()
![]()
![]()
扩展的欧几里得算法
下面介绍欧几里得算法的扩展,它对于后面有限域中的计算极其重要。对于给定的整数a和b,扩展的欧几里得算法不仅可以计算出最大公因子d,而且可以得到两个整数x和y,它们满足如下方程:
![]()
首先应该明白的是x和y一定具有相反的正负号。在详细了解之前让我们先来看看a=42,b=30
时,x和y的一些值。注意gcd(42,30)=6。下面是42x+30y的部分值(本例子取自文献SILV06)

可以观察到,所有的项都可以被6整除。这并不奇怪,因为42和30都可以被6整除,所以每一个形如![]() 的数都是6的倍数。还可以发现,
的数都是6的倍数。还可以发现,![]() 也出现在表中。一般地,可以证明,对于两个给定的整数a和b,可以表示为ax+by的最小正整数等于gcd(a,b)。
也出现在表中。一般地,可以证明,对于两个给定的整数a和b,可以表示为ax+by的最小正整数等于gcd(a,b)。
下面介绍对于给定的a和b,如何扩展欧几里的算法去计算(x,y,d)。假设在每个步骤i都可以得到x和y满足![]() ,最终得到下式:
,最终得到下式:
![]()
![]()
![]()
![]()
![]()
移项得
![]()
同样从i-1行到i-2行,可得到值
![]()
代入移项式有
![]()
然而,我们已经假设![]() ,因此
,因此
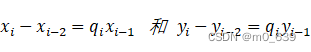
下面举一个例子。令a=1759,b=550,解等式![]()
如图所示:
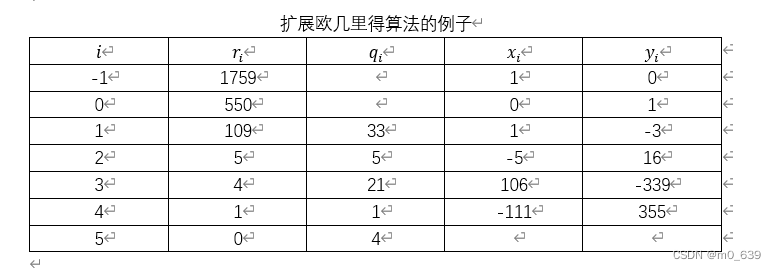
因此,我们有![]()
第四节——素数
数论的核心是素数。
整数p>1是素数,当且仅当它只有因子±1和±p。
任意整数a>1都可以唯一的因式分解为:
![]()
在式子中![]() 均为素数,
均为素数,![]() ,且所有
,且所有![]() 都是正整数。
都是正整数。
下面介绍另一种有用的表示方法。设p是所有素数的集合,则任意正整数a可唯一的表示为:
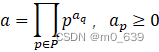
上式的右边是所有可能的素数P之积,对任意整数a其大多数指数![]() 为0。
为0。
我们可以通过列出上述公式中的所有非零指数来唯一的表示一个正整数。
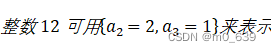
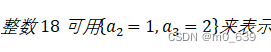
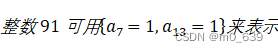
两数相乘即指数对应相加。设![]() ,
,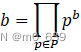 ,定义k=ab。我们知道整数k可以表示为素数方幂的乘积,即
,定义k=ab。我们知道整数k可以表示为素数方幂的乘积,即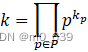 。可以推出对于所有
。可以推出对于所有![]() ,有
,有![]() 成立。
成立。
![]()
![]()
![]()
![]()
从素因子角度看,a整除b,即(a|b)意味着什么呢?由任意整数n形成的![]() 只能被小于等于相同幂次的同一素数
只能被小于等于相同幂次的同一素数![]() 整除(其中
整除(其中![]() )。所以有如下结论。
)。所以有如下结论。
假设![]() ,
,![]() ,如果a|b,那么对任意的
,如果a|b,那么对任意的![]() 有
有![]() 。
。
![]()
![]()
![]()
![]()
若将整数表示为素数之积,则很容易确定两个正整数的最大公因子。
下列关系式总能成立:
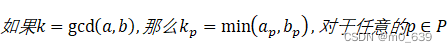
确定一个大数的素数因子并不简单,因此利用上述关系式并不能直接计算最大公因子的实用方法。
第五节费马定理和欧拉定理
费马定律
飞马定理可如下描述,若p是素数,a是正整数,且不能被p整除,则:
![]()
证明:考虑小于p的正整数集合![]() ,用a乘集合中的所有元素并对p取模,得到集合
,用a乘集合中的所有元素并对p取模,得到集合
![]()
因为p不能整除a,所以X的元素不等于0,而且各元素互不相等。为了说明这一点,假设
![]()
其中![]() ,因为a和p互素,因此可将等式两边的a消去,推出
,因为a和p互素,因此可将等式两边的a消去,推出![]() 。最后这个等式不成立,因为j和k都是小于p的正整数。因此X的p-1个元素都是正整数且互不相等。所以说X和
。最后这个等式不成立,因为j和k都是小于p的正整数。因此X的p-1个元素都是正整数且互不相等。所以说X和![]() 的构成相同,只是元素顺序不同。将两个集合的所以元素分别相乘,并对结果模p,有
的构成相同,只是元素顺序不同。将两个集合的所以元素分别相乘,并对结果模p,有
![]()
![]()
费马定理的另一种有用表示形式是:若p是素数且a是任意正整数,则
![]()
请注意定理的第一种形式(![]() )要求a与p互素,而后一种没有这一要求。
)要求a与p互素,而后一种没有这一要求。
![]()
![]()
欧拉函数
在给出欧拉定理之前,我们需要引入数论中一个非常重要的概念,即欧拉函数,它指小于n且于n互素的正整数的个数。习惯上,![]()
求![]() 和
和![]() 的值
的值
因为37是素数,所以从1到36的所有正整数均与37互素,因此![]() =36
=36
要计算![]() ,我们列出所有小于35且与35互素的正整数如下:
,我们列出所有小于35且与35互素的正整数如下:
1, 2, 3, 4, 6, 8, 9, 11 ,12 ,13 ,16 ,17 ,18 ,19 ,22 ,23 ,24 ,26 ,27 ,29 ,31 ,32 ,33, 34
由上可知共有24个数,因此![]() =24
=24
虽然![]() 毫无意义,但我们仍将它定义为1,显然对于素数p,有
毫无意义,但我们仍将它定义为1,显然对于素数p,有
![]()
假设有两个素数p和q,p不等于q,那么对于n=pq,有
![]()
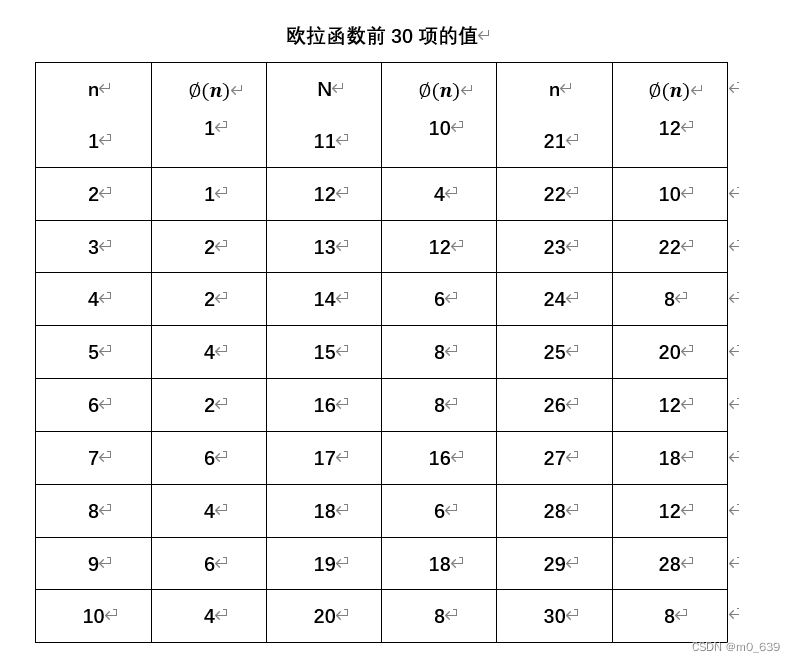
为证明![]() ,考虑集合
,考虑集合![]() ,不与n互素的集合是
,不与n互素的集合是![]() 和
和![]() 。之所以得出这个结果,是因为考虑到任何整数除n都必须除以p或q,因此,与n互素的整数都不会包含p或q:此外,这两个集合是非重叠的:因为p和q都是整数,我们发现第1个集合中不存在为q的整数倍数的数,第2个集合中也不存在一个为p的整数倍数,因此两个集合中共有
。之所以得出这个结果,是因为考虑到任何整数除n都必须除以p或q,因此,与n互素的整数都不会包含p或q:此外,这两个集合是非重叠的:因为p和q都是整数,我们发现第1个集合中不存在为q的整数倍数的数,第2个集合中也不存在一个为p的整数倍数,因此两个集合中共有![]() 个整数,所以
个整数,所以
![]()
![]()
![]()
![]()
欧拉定理
欧拉定理说明,对任意互素的a和n,有
![]()
证明 若n是素数,根据![]() 和费马定理,上式是成立的,但实际上该式对任意整数n都成立,请注意
和费马定理,上式是成立的,但实际上该式对任意整数n都成立,请注意![]() 是指小于n且与n互素的正整数的个数,考虑这些整数所组成的集合
是指小于n且与n互素的正整数的个数,考虑这些整数所组成的集合
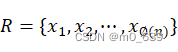
即每个元素都有![]() ,将a与R中每个元素相乘,然后得模n
,将a与R中每个元素相乘,然后得模n
![]()
S是R的一个排列,因为
- a与n互素,且
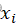 与n互素,所以
与n互素,所以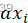 必与n互素,这样S中所有元素均小于n且与n互素。
必与n互素,这样S中所有元素均小于n且与n互素。 - S中没有重复元素。若
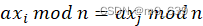 ,则
,则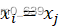
所以集合S是R的一个置换,因此


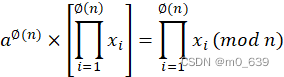
![]()
这里使用的推理和费马定理的证明一样。
![]()
![]()
类似费马定理,欧拉定理的另一种表达形式也很有用。
![]()
同样,和费马定理类似,欧拉定理的第一种形式,要求a与p互素,而后一种没有这一要求。
第六节素性测试
Miller-Rabin算法
Mille和Rabin提出的这一算法是典型的大数素性测试算法,在阐述算法前,我们先给出一些背景,首先,![]() 的奇整数可以如下表示:
的奇整数可以如下表示:
![]()
为了证明这一点,我们注意到(n-1)是一个偶数,接着用2去除(n-1),直到所得结果为奇数,此处共做了k次除法,如果n是二进制数表示,则将改数向右移,直到最右边为1为止,这时可得到结果,此处移动lk次,现在给出我们要用的素数的两个性质。
素数的两个性质
第一个性质叙述如下:若p是素数,a是小于p的正整数,则
![]()
![]()
![]()
![]()
第二个性质如下:设p是大于2的素数,我们有![]() ,其中k>0,q为奇数。设a是整数且
,其中k>0,q为奇数。设a是整数且![]() ,则有下面两个条件之一成立:
,则有下面两个条件之一成立:
![]()
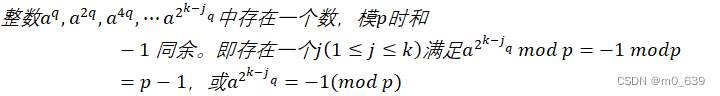
证明 若n是素数,则由费马定理可知,![]() 由于
由于![]() 。因此,如果看下述数列:
。因此,如果看下述数列: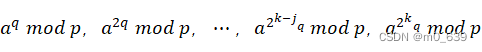
就知道最后的数为1。而且,每个数都是前一个数的平方,因此,下面两条必有一条是正确的:
- 数列的第1个数为1,那么其后的所有数都为1。
- 数列中有些数不为1,但它们的平方模p为1。根据刚才所给出的素数第一性质,我们知道满足这条件的唯一整数为p-1因此,此时数列中必有一个数为p-1。
素数的分布
利用Miller-Rabin测试算法或其他任何素数次算法时,发现一个素数之前会测试多少个整数?由数论中的素数定理可知,n附近的素数分布情况为:平均每In(n)个整数中有一个素数。这样,平均而言,在找到一个素数之前,我们必须测试约In(n)个整数。因为所有偶数肯定不是素数,因此需测试总数个数为0.5×In(n)。然后,这只是平均值,在数轴上的某些位置,素数非常密集;而在其他有些位置,素数非常稀疏。
第七节中国剩余定理
中国剩余定理(CRT)是数论中最有用的定理之一。CRT说明,某一范围内的整数可以通过它的一组剩余类数来重构,这组剩余类数是对该整数用一组两两互素的整数取模得到的。
CRT有几种不同的表示形式,这里给出其中一种最有用的表示形式,令
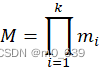
其中![]() 是两两互素的,即对
是两两互素的,即对![]() 。我们可将
。我们可将![]() 中任意一个整数对应一个k元组,该k元组的元素均在
中任意一个整数对应一个k元组,该k元组的元素均在![]() 上,这种对应关系即为
上,这种对应关系即为
![]()
其中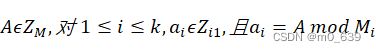 。 CRT说明下列两个断言成立:
。 CRT说明下列两个断言成立:
- 上述是指映射的是
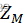 到笛卡尔积的一一对应(称为双射),也就是说,对任何A,
到笛卡尔积的一一对应(称为双射),也就是说,对任何A,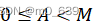 ,有唯一的K元组
,有唯一的K元组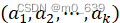 与之对应,其中
与之对应,其中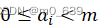 ,并且对任何这样的K元组
,并且对任何这样的K元组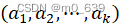 ,
,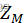 中有唯一的A与之对应。
中有唯一的A与之对应。 -
 中元素上的运算可等价于对应K元素的运算,及笛卡尔积的每个分量上独立的执行运算。
中元素上的运算可等价于对应K元素的运算,及笛卡尔积的每个分量上独立的执行运算。
下面证明第一个断言。由A到![]() 的转换显然是唯一确定的。即只需取
的转换显然是唯一确定的。即只需取![]() 。对给定的
。对给定的![]() ,可如下计算A。对
,可如下计算A。对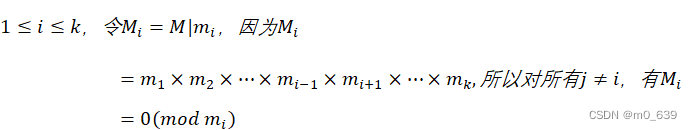 令
令
![]()
根据![]() 的定义,有
的定义,有![]() 与
与![]() 互素,所以
互素,所以![]() 有唯一的模
有唯一的模![]() 的乘法逆元,因此上式是良定的,这样可以得到唯一的
的乘法逆元,因此上式是良定的,这样可以得到唯一的![]() 。计算
。计算
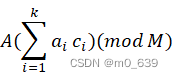
要证明A的产生是正确的,必须证明对 第二个断言与算术运算有关,可从模算术规则推出,及上述第二个断言也可如下描述:若
第二个断言与算术运算有关,可从模算术规则推出,及上述第二个断言也可如下描述:若
![]()
![]()
则
![]()
![]()
![]()
中国剩余定理的用途之一是,它给出了一种方法,使得模M的大数运算转化到相对较小的数的运算,当M为150位或150位以上时,这种方法非常重要,但事先需要分解M.。
第八节离散对数
模n的整数幂
欧拉定理告诉我们,对任何负数的a和n有
![]()
其中欧拉函数![]() 是指小于n且与n互素的正整个数。下面考虑欧拉定理更一般的表示形式。
是指小于n且与n互素的正整个数。下面考虑欧拉定理更一般的表示形式。
![]()
若a与n互素,则至少有一个整数m满足上述式子,即![]() ,我们称使得上述式子成立的最小止幂m为下列之一:
,我们称使得上述式子成立的最小止幂m为下列之一:
-
 的阶
的阶 -
a所属模n的指数
-
a所产生的周期长

上表给出了所有小于19的正整数a模19的各次幂,阴影部分指明了每个底a的幂序列长。
注意:
- 所有序列均以1结束,这与前面的推导是一致的。
- 每一个序列的长度都可以整除
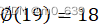 ,也就是说表中的每一行都有整数个子序列。
,也就是说表中的每一行都有整数个子序列。 - 有些序列长为18。这时我们说底a(通过幂运算)生成了模19的非零整数集,并称这样的整数为模数19的本原根。
更一般的我们说,![]() 是一个数所属的模n的可能的最高指数。如果一个数的阶为
是一个数所属的模n的可能的最高指数。如果一个数的阶为![]() ,则称之为n的本源根。本原根的重要之处在于,若a是n的本原根,则其幂
,则称之为n的本源根。本原根的重要之处在于,若a是n的本原根,则其幂
![]()
是(模n)各不相同的,且均与n互素。特别的,对素数p,若a是p的本原根,则
![]()
是(模n)各不相同的。素数19的本原根为2,3,10,13,14和15。
并非所有整数都有本原根。事实上,只有形为2,4,pa和 的整数才有本原根,其中p是任何奇素数,a是正整数,证明并不简单,可参考文献【ORE76】
的整数才有本原根,其中p是任何奇素数,a是正整数,证明并不简单,可参考文献【ORE76】
模算数对数
对于普通正实数,对数函数是指数函数的逆函数,模算术也有类似的函数。
给定一个数,它的对数是满足下列条件的幂,以某个正数(1除以外)为底的该次幂恰好等于给定的这个整数,即对比x和数y
![]()
对数具有下列性质:
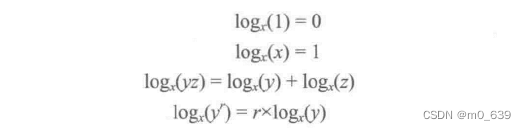
对某素数p(对非素数亦可)的本原根a,a的1到(p-1)的各次幂恰可一次产生1到(p-1)的每一个整数,且仅一次。而对任何整数b,根据模算术的定义,b满足
![]()
因此,对任何整数b和素数p的本原根a,有唯一的幂i使得
![]()
该指数i称为以a为底(模p)的b的离散对数,记为
![]()
请注意下各式:
![]()
![]()
考虑

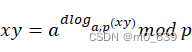
由模乘法的性质有
![]()
![]()
![]()
根据欧拉定理对任何互素的a和n,有
![]()
此外,任何正整数可表示为 ,所以欧拉定理有
,所以欧拉定理有
![]()
将其代入前面的等式,则有
![]()
由此可得
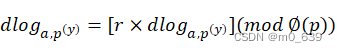
这说明了普通对数和离散对数之间的相似性。
注意,仅当a是m的本原根时,才存在有唯一的以a为底模m的离散对数。
离散对数的计算
考虑
![]()
方程对给定的g,x和p,可直接计算出y,在最坏情况下需执行x次乘法,而且存在计算y的有效算法。
但是,给定y,g和p,计算x一般非常困难(即求离散对数),其难度与RSA中因子分解素数之积的难度的数量级相同。已知最快求模数为素数的离散对数的算法的难度阶为:
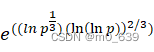
对大数素数而言,该算法是不可行的。
第9节关键术语
双射。因子。最大公因子。阶。合数。欧几里得算法。单位元。素数。交换性。欧拉定理。指标。本原根。中国剩余定理。欧拉函数。模运算。互素。离散对数。费马定理。模量。余数。
本文主要参考文献
【ORE76】【LEVE90】【SILVO6】
注:
- 有限集s的一个排列,是指s中某个给定顺序的元素,在该顺序中每个元素只出现一次。
- 费马定理通常指的是费马小定理。
- 两个数若无公共素因子,即它们的唯一公因子为1,则称这两个数是互素的,也就是说,这两个数的最大公因子为1,则它们是互素的。






















 774
774











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








