匈牙利算法和KM算法都可用来解决任务分配问题(亦称指派问题):假设有n名员工以及n份工作,一个人只能完成一项任务且能完成的任务各不相同。问如何安排员工才能使效率达到最大。
用大白话来描述二分图:二分图可划分为两个集合{员工},{工作},两个集合之间的元素可以相连,同一个集合内的元素不能相连。

如图的二分图匹配问题可以用匈牙利算法解决。
现在我们思考另外一个问题:上图中我们默认A、B、C的工作效率是一样的(即A员工或者B员工完成工作a的时间是相等的),这种情况在现实生活中只是少数。那么A、B、C员工完成不同的工作有不同效率的话,应该如何得到最优匹配呢?

KM算法就是用来解决二分图最大权分配问题,其步骤如下所示:
①左边的顶点赋值为最大权重,右边顶点赋值为0。

②匹配。匹配的原则是只匹配与最大效率相等的边。如果匹配失败,那么参与匹配的所有左顶点的值-1,右顶点+1,直至匹配完成。
按照此约定,我们对A进行匹配:连接Ac,匹配成功!
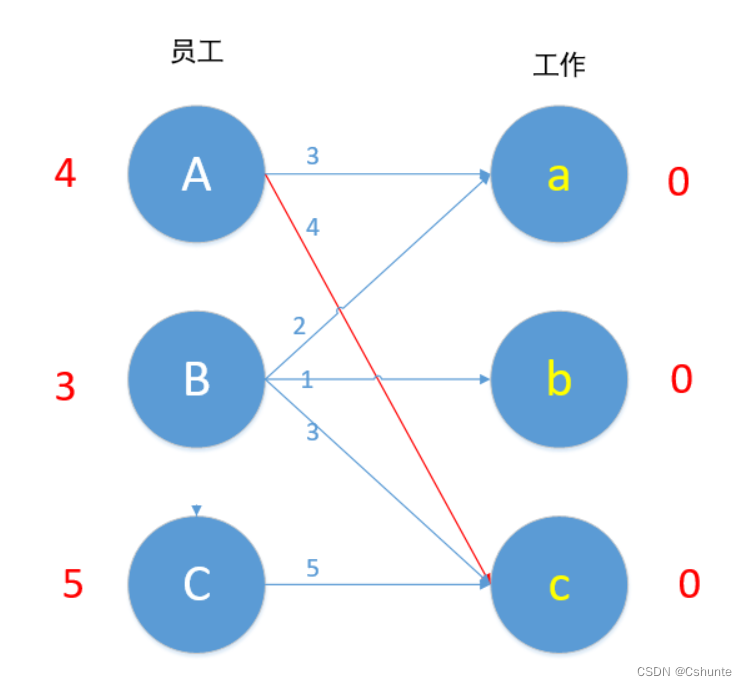
接下来我们对B员工进行匹配。但是我们发现,与B最大效率匹配的边只有Bc,而c已经和A进行匹配了,怎么办呢?正常的思路是看看A还有没有其他符合的边,只可惜没有。按照匹配的原则,需要对A、B的效率-1,对c+1。这样一来,A的效率更新为3,B的效率更新为2,c的值变为1。

通过-1、+1操作,Ac、Bc仍然是可以匹配的边:3+1=4,2+1=3。除此之外还给我们带来了新的选择:Aa和Ba。
这样一来,B就可以在不改变A工作的前提下找到工作了。匹配Ba成功!

现在我们来匹配C。由于5+1≠5,且c已经和A匹配了。于是我们找到A,看看A还有没有别的选择。我们发现A出了可以和c匹配(3+1=4),还可以和a进行匹配(3+0=3)。正想匹配Aa的时候又发现a已经和B进行匹配了。于是我们找到B,看看B还有没有其他符合的匹配。但是此时B表示自己能力有限,可谓是爱莫能助啊,自己只能和a进行匹配了。那么参与到此次"争端"的结点有:A、B、C、a、c,交给匹配原则进行”处置“。
(这步有点套娃,原理搞懂就不觉得难了。)
更新各值如图所示:
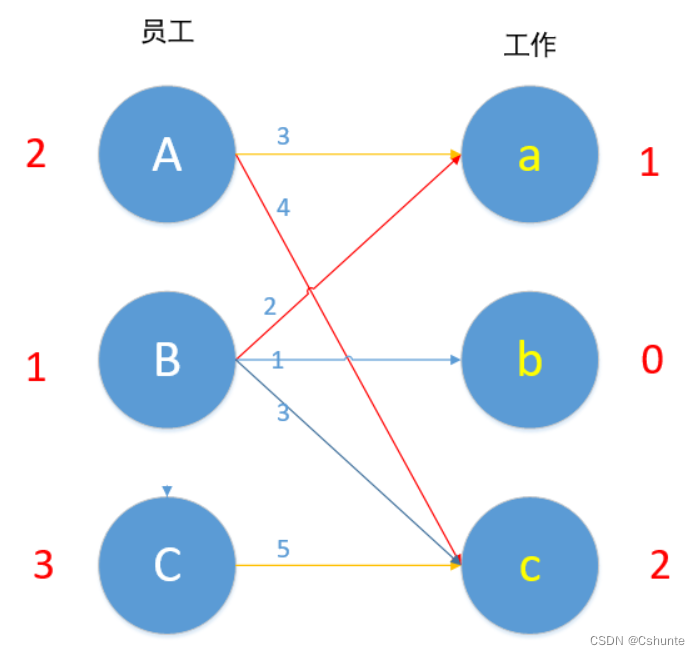
对于现在来说,B就可以匹配了!(1+0=1)
由匈牙利算法的取反操作(下方有解释),即可得到最终匹配。

这就是KM算法的整个过程,每次给一个顶点找到最大权重边,配合匈牙利算法找到最大匹配,从而得到完美匹配。
匈牙利算法处理”冲突问题“:
在Aa已经匹配成功的前提下,若B只能匹配a,那么匈牙利算法告诉我们可以通过一条增广路径,通过取反操作,我们就能匹配更多的点。
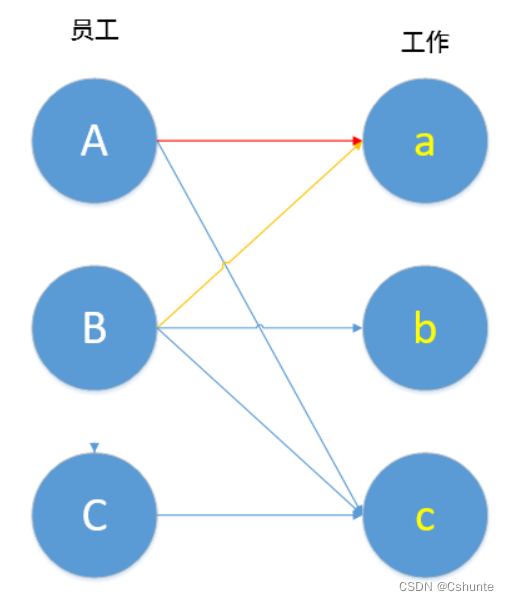
增广路径的定义:从一个未匹配的顶点开始,经过若干个匹配顶点,最后到达对面集合的一个未匹配顶点的路径,也就是说,这条路径将两个不同集合的两个未匹配顶点通过一系列匹配顶点相连。
在此题中,A还可以和c匹配,就产生了增广路:B--a--A--c,经过取反操作之后,匹配更新为:
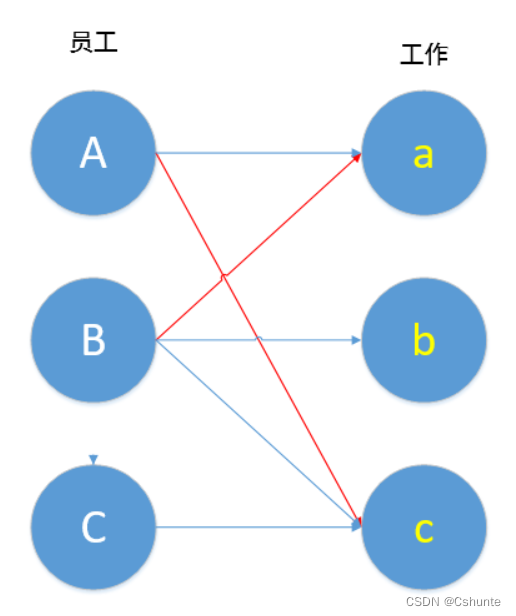
由这一轮操作,增加了一条匹配边,解决了矛盾。这就是匈牙利算法增广路径取反的巧妙之处!
我们可以在出现冲突的时候寻找增广路径,从而找到最优匹配。








 KM算法是解决二分图最大权分配问题的有效方法,尤其在存在不同效率的情况下。它结合匈牙利算法,通过调整顶点权重,寻找增广路径,实现最优匹配。在匹配过程中,当遇到冲突时,通过取反操作更新匹配状态,最终找到完美匹配的解决方案。这一过程涉及到多次匹配尝试和权重更新,确保每个员工都能被合理高效地分配到任务。
KM算法是解决二分图最大权分配问题的有效方法,尤其在存在不同效率的情况下。它结合匈牙利算法,通过调整顶点权重,寻找增广路径,实现最优匹配。在匹配过程中,当遇到冲突时,通过取反操作更新匹配状态,最终找到完美匹配的解决方案。这一过程涉及到多次匹配尝试和权重更新,确保每个员工都能被合理高效地分配到任务。

















 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








