原来机器学习那么简单——K近邻回归

引言：
在正文开始之前，首先给大家介绍一个不错的人工智能学习教程：https://www.captainbed.cn/bbs。其中包含了机器学习、深度学习、强化学习等系列教程，感兴趣的读者可以自行查阅。

---

一、什么是K近邻回归？

K近邻回归（K-Nearest Neighbors Regression，简称KNN回归）是一种简单直观的机器学习算法。KNN回归通过寻找样本空间中与目标点最接近的K个邻居，利用这些邻居的平均值或加权平均值来预测目标点的值。KNN回归属于非参数模型，因为它不对数据的分布做出假设，也不需要训练过程。

二、K近邻回归的原理

KNN回归的核心思想非常直观，即“相似的样本具有相似的输出”。具体步骤如下：

1. 计算距离：对于待预测的样本点，计算其与训练集中每一个样本点之间的距离。常用的距离度量包括欧氏距离（Euclidean Distance）、曼哈顿距离（Manhattan Distance）等。

   欧氏距离的计算公式为：
   $$d(x_i,x_j)=\sqrt{\sum _{k=1}^n(x_{i,k}-x_{j,k}{)}^2}$$
   其中，$ x_i $ 和 $ x_j $ 分别是两个样本点的特征向量，$ n $ 是特征的维数。

2. 选择K个邻居：根据计算得到的距离，选择距离待预测样本点最近的K个邻居。

3. 计算预测值：根据选中的K个邻居的输出值，计算待预测样本点的输出值。常用的方法包括简单平均和加权平均。如果是简单平均，则预测值为K个邻居的输出值的算术平均：

   $$\hat{y}=\frac{1}{K}\sum _{i=1}^K{y}_i$$
   其中，$ y_i $ 是第 $i$个邻居的输出值。

   如果采用加权平均，则预测值为K个邻居的加权平均值，权重通常为邻居与待预测样本点距离的倒数：

   $$\hat{y}=\frac{{\sum }_{i=1}^K\frac{1}{d(x,x_i)}{y}_i}{{\sum }_{i=1}^K\frac{1}{d(x,x_i)}}$$
   其中，$ d(x, x_i) $ 是待预测样本点与第 $ i $ 个邻居的距离。

三、K近邻回归的优缺点

优点：

• 简单直观：算法思想简单，容易理解和实现。
• 无模型假设：KNN回归不对数据的分布做任何假设，适用于各种数据分布。
• 高灵活性：由于无需训练过程，KNN回归可以处理在线学习问题，也可以随时加入新的数据。

缺点：

• 计算复杂度高：对于大规模数据集，计算每个样本点的距离代价较高，影响预测效率。
• 维度灾难：随着特征维数的增加，样本之间的距离变得越来越难以区分，导致预测效果下降。
• 对异常值敏感：KNN回归直接依赖于邻居的输出值，如果邻居中存在异常值，可能会严重影响预测结果。

四、案例分析

在这一部分，我们还是使用加州房价数据集来演示如何应用K近邻回归算法进行预测。加州房价数据集包含了加州的街区信息，每个街区有多项特征，包括人口、收入、房屋年龄等。目标是根据这些特征预测该街区的房屋中位数价格。

1. 数据加载与预处理：

   • 加载加州房价数据集并进行标准化处理，确保所有特征都在相同的尺度上。
   • 将数据集划分为训练集和测试集，比例为8:2。

2. 模型训练：

   • 使用KNeighborsRegressor创建一个K近邻回归模型，选择K=5，即考虑最近的5个邻居。
   • 用训练集的数据来训练模型。

3. 模型预测：

   • 利用训练好的模型对测试集进行预测，并计算均方误差（MSE）作为模型性能的评估指标。

代码实现：

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.datasets import fetch_california_housing
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.neighbors import KNeighborsRegressor
from sklearn.metrics import mean_squared_error

# 加载加州房价数据集
california = fetch_california_housing()
X = california.data
y = california.target

# 数据标准化
scaler = StandardScaler()
X_scaled = scaler.fit_transform(X)

# 划分训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(X_scaled, y, test_size=0.2, random_state=42)

# 创建K近邻回归模型并训练
knn = KNeighborsRegressor(n_neighbors=5)
knn.fit(X_train, y_train)

# 预测测试集
y_pred = knn.predict(X_test)

# 计算均方误差
mse = mean_squared_error(y_test, y_pred)
print(f"测试集的均方误差: {mse:.2f}")

# 可视化结果
plt.figure(figsize=(10, 6))
plt.scatter(y_test, y_pred, edgecolor='k', alpha=0.7)
plt.plot([min(y_test), max(y_test)], [min(y_test), max(y_test)], 'r--', lw=3)
plt.xlabel("真实房价")
plt.ylabel("预测房价")
plt.title("K近邻回归预测结果")
plt.show()

结果分析：

测试集的均方误差: 0.43。

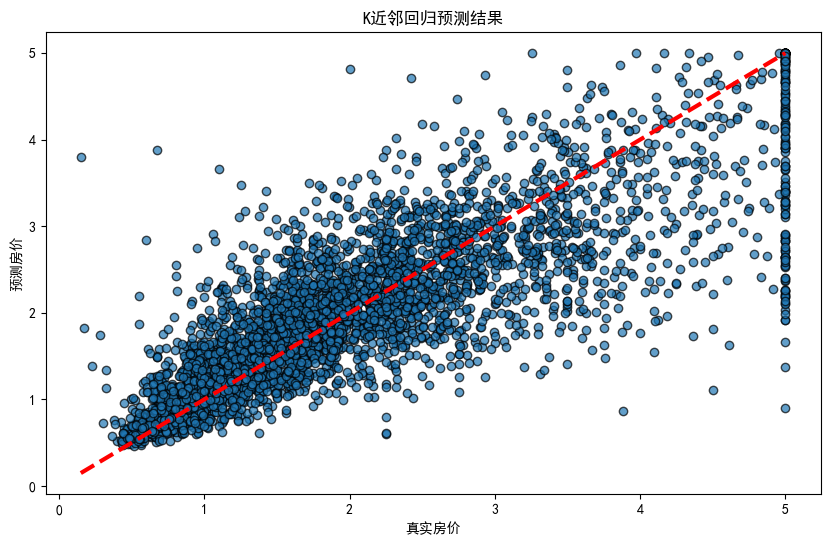
通过散点图，可以看到模型预测的房价与真实房价之间的关系。

五、总结

K近邻回归是一种简单且易于理解的回归算法，适合用于小规模数据集或需要在线更新模型的场景。然而，在使用KNN回归时，需要考虑数据的维数和计算复杂度，并对异常值进行处理，以确保模型的预测效果。