强化学习之DDPG算法

前言：
在正文开始之前，首先给大家介绍一个不错的人工智能学习教程：https://www.captainbed.cn/bbs。其中包含了机器学习、深度学习、强化学习等系列教程，感兴趣的读者可以自行查阅。

---

一、算法介绍

深度确定性策略梯度 （Deep Deterministic Policy Gradient，简称DDPG） 算法是一种基于策略梯度的方法，结合了深度神经网络和确定性策略的优势。它特别适用于具有连续动作空间的控制任务，如机械臂控制、自动驾驶等。DDPG算法通过同时训练一个演员网络（Actor）和一个评论家网络（Critic），实现对策略的优化。

主要特点包括：

• 确定性策略：与随机策略不同，DDPG使用确定性策略，直接输出给定状态下的最优动作。
• 经验回放（Replay Buffer）：通过存储经验样本，打破样本间的相关性，提升训练稳定性。
• 目标网络（Target Networks）：使用延迟更新的目标网络，减少训练过程中的震荡和不稳定。

二、算法原理

2.1 网络结构

DDPG算法由两个主要网络组成：

• 演员网络（Actor）：参数为${\theta }^{\mu }$，用于确定性地选择动作。

  $$a=\mu (s|{\theta }^{\mu })$$

• 评论家网络（Critic）：参数为${\theta }^Q$，用于估计给定状态-动作对的Q值。

  $$Q(s,a|{\theta }^Q)$$

此外，还存在两个目标网络，分别对应演员和评论家网络，参数为${\theta }^{{\mu }^{\prime }}$和${\theta }^{Q^{\prime }}$，用于计算目标Q值。

2.2 经验回放

经验回放池$\mathcal{D}$用于存储经验元组$(s_t,a_t,r_t,s_{t+1})$。在每次训练迭代中，算法从$\mathcal{D}$中随机采样一个小批量样本，打破数据间的相关性，提高训练效率和稳定性。

2.3 目标网络的更新

目标网络的参数通过软更新方式更新：

$${\theta }^{{\mu }^{\prime }}\leftarrow \tau {\theta }^{\mu }+(1-\tau ){\theta }^{{\mu }^{\prime }}$$

$${\theta }^{Q^{\prime }}\leftarrow \tau {\theta }^Q+(1-\tau ){\theta }^{Q^{\prime }}$$

其中，$\tau$是软更新的步长，通常取值较小，如$0.001$。

2.4 损失函数与优化

• 评论家网络的损失函数采用均方误差（MSE）：

  $$L=\frac{1}{N}\sum _{i=1}^N{\left(y_i-Q(s_i,a_i|{\theta }^Q)\right)}^2$$

  其中，

  $$y_i=r_i+\gamma Q^{\prime }(s_{i+1},{\mu }^{\prime }(s_{i+1}|{\theta }^{{\mu }^{\prime }})|{\theta }^{Q^{\prime }})$$

• 演员网络的损失函数通过最大化Q值来优化策略：

  $$J=-\frac{1}{N}\sum _{i=1}^{N}Q(s_i,\mu (s_i|{\theta }^{\mu })|{\theta }^Q)$$

2.5 算法流程

1. 初始化演员网络$\mu (s|{\theta }^{\mu })$和评论家网络$Q(s,a|{\theta }^Q)$，以及对应的目标网络${\mu }^{\prime }$和$Q^{\prime }$。
2. 初始化经验回放池$\mathcal{D}$。
3. 对于每个回合：
   • 在环境中选择动作$a_t=\mu (s_t|{\theta }^{\mu })+{\mathcal{N}}_t$，其中${\mathcal{N}}_t$为噪声，用于探索。
   • 执行动作$a_t$，观察奖励$r_t$和下一个状态$s_{t+1}$。
   • 存储经验$(s_t,a_t,r_t,s_{t+1})$到$\mathcal{D}$。
   • 从$\mathcal{D}$中随机采样一个小批量样本。
   • 计算目标Q值$y_i$。
   • 更新评论家网络参数${\theta }^Q$，最小化损失$L$。
   • 更新演员网络参数${\theta }^{\mu }$，最大化$J$。
   • 软更新目标网络参数${\theta }^{{\mu }^{\prime }}$和${\theta }^{Q^{\prime }}$。
4. 重复以上步骤，直至收敛。

三、案例分析

在本节中，我们将通过在Pendulum-v0环境中应用DDPG算法，展示其具体实现过程。该环境的目标是让倒立摆尽可能长时间地保持直立状态，涉及连续动作空间。

3.1 环境简介

• 状态空间：摆锤的角度、角速度，共3个维度。
• 动作空间：施加的力矩，范围为$[-2,2]$。
  

3.2 实现代码

以下是使用PyTorch实现的DDPG算法在Pendulum-v0环境中的部分代码。

# 经验回放池
class ReplayBuffer:
    def __init__(self, buffer_size, batch_size, seed):
        self.memory = deque(maxlen=buffer_size)
        self.batch_size = batch_size
        self.seed = random.seed(seed)
    
    def add(self, state, action, reward, next_state, done):
        self.memory.append((state, action, reward, next_state, done))
    
    def sample(self):
        experiences = random.sample(self.memory, k=self.batch_size)
        
        states = torch.FloatTensor([e[0] for e in experiences]).to(device)
        actions = torch.FloatTensor([e[1] for e in experiences]).to(device)
        rewards = torch.FloatTensor([e[2] for e in experiences]).unsqueeze(1).to(device)
        next_states = torch.FloatTensor([e[3] for e in experiences]).to(device)
        dones = torch.FloatTensor([float(e[4]) for e in experiences]).unsqueeze(1).to(device)
        
        return states, actions, rewards, next_states, dones
    
    def __len__(self):
        return len(self.memory)

# 神经网络定义
def hidden_init(layer):
    fan_in = layer.weight.data.size()[0]
    lim = 1. / np.sqrt(fan_in)
    return (-lim, lim)

class PolicyNet(nn.Module):
    def __init__(self, state_dim, hidden_dim, action_dim, action_bound):
        super(PolicyNet, self).__init__()
        self.fc1 = nn.Linear(state_dim, hidden_dim)
        self.fc2 = nn.Linear(hidden_dim, action_dim)
        self.action_bound = action_bound  # 动作最大值
    
        # 初始化权重
        self.fc1.weight.data.uniform_(*hidden_init(self.fc1))
        self.fc2.weight.data.uniform_(-3e-3, 3e-3)
    
    def forward(self, x):
        x = F.relu(self.fc1(x))
        return torch.tanh(self.fc2(x)) * self.action_bound

class QValueNet(nn.Module):
    def __init__(self, state_dim, hidden_dim, action_dim):
        super(QValueNet, self).__init__()
        self.fc1 = nn.Linear(state_dim + action_dim, hidden_dim)
        self.fc2 = nn.Linear(hidden_dim, hidden_dim)
        self.fc_out = nn.Linear(hidden_dim, 1)

        # 初始化权重
        self.fc1.weight.data.uniform_(*hidden_init(self.fc1))
        self.fc2.weight.data.uniform_(*hidden_init(self.fc2))
        self.fc_out.weight.data.uniform_(-3e-3, 3e-3)
    
    def forward(self, x, a):
        cat = torch.cat([x, a], dim=1)  # 拼接状态和动作
        x = F.relu(self.fc1(cat))
        x = F.relu(self.fc2(x))
        return self.fc_out(x)

# DDPG智能体
class DDPGAgent:
    ''' DDPG算法 '''
    def __init__(self, state_dim, hidden_dim, action_dim, action_bound, sigma, actor_lr, critic_lr, tau, gamma, device):
        self.actor = PolicyNet(state_dim, hidden_dim, action_dim, action_bound).to(device)
        self.critic = QValueNet(state_dim, hidden_dim, action_dim).to(device)
        self.target_actor = PolicyNet(state_dim, hidden_dim, action_dim, action_bound).to(device)
        self.target_critic = QValueNet(state_dim, hidden_dim, action_dim).to(device)
        # 初始化目标网络并设置和主网络相同的参数
        self.target_critic.load_state_dict(self.critic.state_dict())
        self.target_actor.load_state_dict(self.actor.state_dict())
        self.actor_optimizer = optim.Adam(self.actor.parameters(), lr=actor_lr)
        self.critic_optimizer = optim.Adam(self.critic.parameters(), lr=critic_lr, weight_decay=WEIGHT_DECAY)
        self.gamma = gamma
        self.sigma = sigma  # 高斯噪声的标准差
        self.tau = tau  # 目标网络软更新参数
        self.action_dim = action_dim
        self.device = device

    def take_action(self, state):
        state = torch.tensor([state], dtype=torch.float).to(self.device)
        self.actor.eval()
        with torch.no_grad():
            action = self.actor(state).cpu().data.numpy().flatten()
        self.actor.train()
        # 给动作添加噪声，增加探索
        action += self.sigma * np.random.randn(self.action_dim)
        return np.clip(action, -self.actor.action_bound, self.actor.action_bound)

    def soft_update(self, net, target_net):
        for target_param, param in zip(target_net.parameters(), net.parameters()):
            target_param.data.copy_(param.data * self.tau + target_param.data * (1.0 - self.tau))

    def update(self, replay_buffer):
        if len(replay_buffer) < BATCH_SIZE:
            return
        
        states, actions, rewards, next_states, dones = replay_buffer.sample()

        # 更新Critic网络
        with torch.no_grad():
            next_actions = self.target_actor(next_states)
            Q_targets_next = self.target_critic(next_states, next_actions)
            Q_targets = rewards + (self.gamma * Q_targets_next * (1 - dones))
        Q_expected = self.critic(states, actions)
        critic_loss = F.mse_loss(Q_expected, Q_targets)
        
        self.critic_optimizer.zero_grad()
        critic_loss.backward()
        self.critic_optimizer.step()

        # 更新Actor网络
        actor_loss = -torch.mean(self.critic(states, self.actor(states)))
        
        self.actor_optimizer.zero_grad()
        actor_loss.backward()
        self.actor_optimizer.step()

        # 软更新目标网络
        self.soft_update(self.critic, self.target_critic)
        self.soft_update(self.actor, self.target_actor)

3.3 运行结果

Episode 10	Average Score: -1623.12
Episode 20	Average Score: -1536.40
Episode 30	Average Score: -1287.98
Episode 40	Average Score: -1021.30
Episode 50	Average Score: -995.55
Episode 60	Average Score: -401.11
Episode 70	Average Score: -311.09
Episode 80	Average Score: -433.98
Episode 90	Average Score: -122.43
Episode 100	Average Score: -125.27
Episode 110	Average Score: -122.54
Episode 120	Average Score: -122.86
Episode 130	Average Score: -122.51
Episode 140	Average Score: -123.11
Episode 150	Average Score: -122.93
Episode 160	Average Score: -127.22
Episode 170	Average Score: -146.53
Episode 180	Average Score: -138.31
Episode 190	Average Score: -119.34
Episode 200	Average Score: -118.65

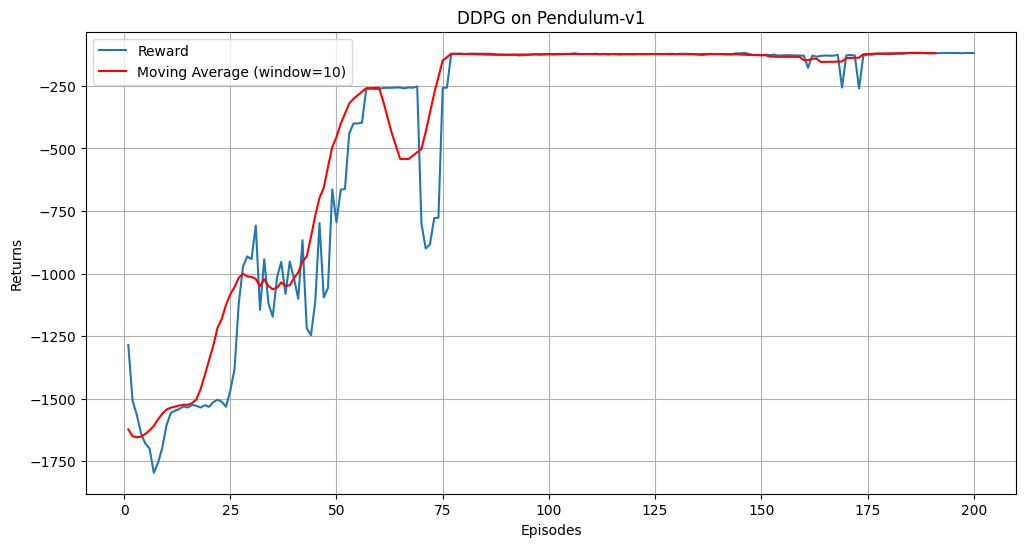
在Pendulum-v0环境中，DDPG智能体经过200个回合的训练后，奖励曲线应逐渐上升，表明智能体的策略在不断优化。滑动平均曲线更平滑，能够更清晰地反映训练趋势。

四、总结

DDPG算法通过结合演员-评论家架构、经验回放和目标网络等技术，有效地解决了连续动作空间中的强化学习问题。在Pendulum-v0环境中的应用展示了其强大的学习能力和策略优化效果。随着研究的深入，DDPG及其衍生算法在更多复杂任务中的应用前景广阔。