强化学习DDPG算法

原创已于 2025-04-19 22:26:05 修改 · 2.9k 阅读

39 ·

CC 4.0 BY-SA版权

文章标签：

#算法 #机器学习 #深度学习 #人工智能

于 2025-04-03 15:58:41 首次发布

强化学习专栏收录该内容

18 篇文章

订阅专栏

DDPG（Deep Deterministic Policy Gradient）算法详解

在这里插入图片描述

1. 背景与动机

问题场景：DDPG 是为解决连续动作空间的强化学习问题而设计的（如机器人控制、自动驾驶），而传统DQN仅适用于离散动作空间。
DQN的局限性：
- DQN通过Q-learning框架选择离散动作（如“左/右”），但无法处理连续动作（如“方向盘转动角度”）。
- 高维连续动作空间中，DQN需要遍历所有可能的动作计算Q值，计算复杂度爆炸。
DPG的启发：
- Deterministic Policy Gradient（DPG）是一种直接优化确定性策略的方法（输出确定动作，而非动作的概率分布），适用于连续控制。
- DDPG将DPG与深度神经网络结合，并引入DQN的经验回放和目标网络技术，提升稳定性和样本效率。

2. DDPG核心原理

DDPG属于Actor-Critic架构，结合了策略梯度（Policy Gradient）和值函数近似（Q-learning）。

2.1 网络结构

Actor网络（策略网络）：
- 输入：状态（State）
- 输出：确定性动作（Action）
- 目标：直接输出最优动作，最大化Q值。
Critic网络（价值网络）：
- 输入：状态（State） + 动作（Action）
- 输出：Q值（评估当前状态动作对的长期收益）
- 目标：准确估计Q值，指导Actor更新。

2.2 核心思想

确定性策略梯度：
策略函数为确定性函数： $\mu(s|\theta^\mu)$
策略梯度公式：
$\nabla_{\theta^\mu} J \approx \mathbb{E}_{s \sim \rho^\beta} \left[ \nabla_a Q(s,a|\theta^Q) \big|_{a=\mu(s|\theta^\mu)} \nabla_{\theta^\mu} \mu(s|\theta^\mu) \right]$
通过链式法则，Critic的Q值梯度指导Actor更新策略。
目标网络与软更新：
- 使用独立的目标Actor网络（参数 $θμ′\theta^{\mu'}$ ）和目标Critic网络（参数 $θQ′\theta^{Q'}$ ），缓解训练不稳定性。
软更新公式：
$\theta_{target} \leftarrow \tau \theta + (1-\tau)\theta_{target} \quad (\tau \ll 1, \text{如} 0.001)$

2.3 算法流程

初始化：
- Actor当前网络 $μ(s∣θμ)\mu(s|\theta^\mu)$ 和 Critic当前网络 $Q(s,a∣θQ)Q(s,a|\theta^Q)$
- 目标网络 $μ′(s∣θμ′)\mu'(s|\theta^{\mu'})$ 和 $Q′(s,a∣θQ′)Q'(s,a|\theta^{Q'})$ （初始参数相同）
- 经验回放池（Replay Buffer）
交互与采样：
- Actor根据当前策略选择动作 $at=μ(st∣θμ)+Nta_t = \mu(s_t|\theta^\mu) + \mathcal{N}_t$ （加入探索噪声，如OU噪声）
- 执行动作 $a_t$ ，观察奖励 $r_{t+1}$ 和下一状态 $s_{t+1}$
- 存储 $s_t, a_t, r_{t+1}, s_{t+1})$ 到经验池
网络更新：
- 从经验池采样小批量数据
- Critic更新最小化贝尔曼误差：
  - 计算目标Q值： $yi=ri+γQtarget(si+1,μtarget(si+1))y_i = r_i + \gamma Q_{target}(s_{i+1}, \mu_{target}(s_{i+1}))$
  - 最小化均方误差损失： $Lcritic=1N∑i(yi−Q(si,ai))2\mathcal{L}_{critic} = \frac{1}{N} \sum_i (y_i - Q(s_i,a_i))^2$
- Actor更新：
  - 通过策略梯度上升(确定性策略梯度定理)更新Actor参数：最大化 $\mu(s|\theta^\mu)|\theta^Q)$
    $\nabla_{\theta_\mu}\mathcal{J}\approx\mathbb{E}\left[ \nabla_aQ(s,a)|_{a=\mu(s)} \cdot \nabla_{\theta_\mu}\mu(s)\right]$
目标网络软更新：
- 定期以微小步长更新目标网络参数（ $τ≪1\tau \ll 1$ ）

3. DDPG的优势与改进

3.1 与DQN的区别

特性	DDPG	DQN
动作空间	连续（直接输出动作值）	离散（选择Q值最大的动作）
策略类型	确定性策略（Actor直接输出动作）	隐式策略（通过Q值选择动作）
网络架构	Actor-Critic（双网络协同）	单一Q网络
探索方式	通过动作噪声（如OU过程）	ε-greedy随机选择动作
目标网络更新	软更新（参数缓慢混合）	硬更新（定期复制参数）

3.2 DDPG的改进

连续动作空间：直接输出连续动作值，解决DQN的维度灾难问题。
确定性策略梯度：相比随机策略梯度（如A3C），训练更高效，方差更低。
目标网络与经验回放：继承DQN的稳定性技术，缓解Q-learning的高估问题。
探索与利用的平衡：通过添加噪声（如Ornstein-Uhlenbeck过程）实现探索，避免策略陷入局部最优。

4. DDPG的挑战与后续改进

训练不稳定：对超参数敏感（如学习率、噪声参数）。
过估计问题：Critic可能高估Q值，导致策略偏差。
改进算法：
TD3（Twin Delayed DDPG）：
- 使用双Critic网络取最小值，减少Q值高估。
- 延迟策略更新（Actor更新频率低于Critic）。
- 添加目标策略平滑噪声。

5. 应用场景

机器人控制（如机械臂抓取）
自动驾驶（连续转向和油门控制）
物理仿真（如MuJoCo环境中的复杂运动任务）

6. 代码demo

import torch
import torch.nn as nn
import torch.optim as optim
import numpy as np
import gym

# Actor网络（策略网络）
class Actor(nn.Module):
    def __init__(self, state_dim, action_dim, max_action):
        super(Actor, self).__init__()
        self.net = nn.Sequential(
            nn.Linear(state_dim, 256),
            nn.ReLU(),
            nn.Linear(256, 256),
            nn.ReLU(),
            nn.Linear(256, action_dim),
            nn.Tanh()  # 输出范围[-1, 1]
        )
        self.max_action = max_action  # 缩放动作到环境范围

    def forward(self, state):
        return self.max_action * self.net(state)

# Critic网络（Q值网络）
class Critic(nn.Module):
    def __init__(self, state_dim, action_dim):
        super(Critic, self).__init__()
        self.net = nn.Sequential(
            nn.Linear(state_dim + action_dim, 256),
            nn.ReLU(),
            nn.Linear(256, 256),
            nn.ReLU(),
            nn.Linear(256, 1)
        )

    def forward(self, state, action):
        x = torch.cat([state, action], dim=1)
        return self.net(x)

# DDPG Agent
class DDPG:
    def __init__(self, state_dim, action_dim, max_action, device='cuda', tau=0.005, gamma=0.99):
        self.actor = Actor(state_dim, action_dim, max_action).to(device)
        self.actor_target = Actor(state_dim, action_dim, max_action).to(device)
        self.actor_target.load_state_dict(self.actor.state_dict())
        self.actor_optimizer = optim.Adam(self.actor.parameters(), lr=1e-4)

        self.critic = Critic(state_dim, action_dim).to(device)
        self.critic_target = Critic(state_dim, action_dim).to(device)
        self.critic_target.load_state_dict(self.critic.state_dict())
        self.critic_optimizer = optim.Adam(self.critic.parameters(), lr=1e-3)

        self.tau = tau  # 软更新系数
        self.gamma = gamma  # 折扣因子
        self.device = device

    def select_action(self, state, noise=None):
        state = torch.FloatTensor(state).unsqueeze(0).to(self.device)
        action = self.actor(state).cpu().data.numpy().flatten()
        if noise is not None:
            action += noise.sample()
        return np.clip(action, -self.actor.max_action, self.actor.max_action)

    def update(self, batch):
        states, actions, rewards, next_states, dones = batch

        # 转换为Tensor
        states = torch.FloatTensor(states).to(self.device)
        actions = torch.FloatTensor(actions).to(self.device)
        rewards = torch.FloatTensor(rewards).unsqueeze(1).to(self.device)
        next_states = torch.FloatTensor(next_states).to(self.device)
        dones = torch.FloatTensor(dones).unsqueeze(1).to(self.device)

        # Critic更新
        with torch.no_grad():
            next_actions = self.actor_target(next_states)
            target_q = self.critic_target(next_states, next_actions)
            target_q = rewards + (1 - dones) * self.gamma * target_q

        current_q = self.critic(states, actions)
        critic_loss = nn.MSELoss()(current_q, target_q)

        self.critic_optimizer.zero_grad()
        critic_loss.backward()
        self.critic_optimizer.step()

        # Actor更新
        actor_loss = -self.critic(states, self.actor(states)).mean()

        self.actor_optimizer.zero_grad()
        actor_loss.backward()
        self.actor_optimizer.step()

        # 软更新目标网络
        for param, target_param in zip(self.actor.parameters(), self.actor_target.parameters()):
            target_param.data.copy_(self.tau * param.data + (1 - self.tau) * target_param.data)
        for param, target_param in zip(self.critic.parameters(), self.critic_target.parameters()):
            target_param.data.copy_(self.tau * param.data + (1 - self.tau) * target_param.data)

        return critic_loss.item(), actor_loss.item()

# 经验回放缓冲区
class ReplayBuffer:
    def __init__(self, max_size):
        self.buffer = []
        self.max_size = max_size

    def add(self, state, action, reward, next_state, done):
        if len(self.buffer) >= self.max_size:
            self.buffer.pop(0)
        self.buffer.append((state, action, reward, next_state, done))

    def sample(self, batch_size):
        indices = np.random.choice(len(self.buffer), batch_size, replace=False)
        states, actions, rewards, next_states, dones = zip(*[self.buffer[i] for i in indices])
        return (
            np.array(states),
            np.array(actions),
            np.array(rewards),
            np.array(next_states),
            np.array(dones)
        )

# 训练示例
env = gym.make('Pendulum-v0')
state_dim = env.observation_space.shape[0]
action_dim = env.action_space.shape[0]
max_action = float(env.action_space.high[0])

device = 'cuda' if torch.cuda.is_available() else 'cpu'
agent = DDPG(state_dim, action_dim, max_action, device=device)
buffer = ReplayBuffer(max_size=100000)

max_episodes = 1000
batch_size = 64
ou_noise = OUNoise(action_dim)  # 实现略，可用高斯噪声替代

for episode in range(max_episodes):
    state = env.reset()
    episode_reward = 0
    while True:
        action = agent.select_action(state, ou_noise)
        next_state, reward, done, _ = env.step(action)
        buffer.add(state, action, reward, next_state, done)
        state = next_state
        episode_reward += reward

        if len(buffer.buffer) > batch_size:
            batch = buffer.sample(batch_size)
            critic_loss, actor_loss = agent.update(batch)
        
        if done:
            break
    print(f"Episode: {episode}, Reward: {episode_reward}")

7. 策略梯度扩展理解:随机性策略梯度 vs 确定性策略梯度

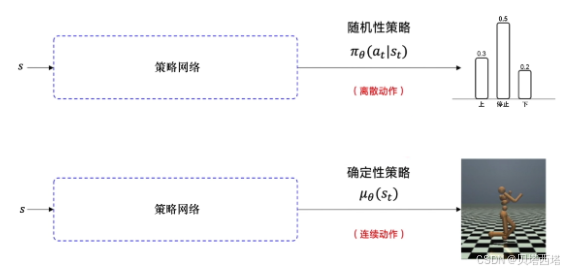
在这里插入图片描述

7.1. 随机策略梯度（Stochastic Policy Gradient）

原理

策略形式：策略输出动作的概率分布，即 $π(a∣s;θ)\pi(a|s; \theta)$ 。
目标函数：最大化期望回报 $J(θ)=Eτ∼π[∑t=0Tγtrt]J(\theta) = \mathbb{E}_{\tau \sim \pi} \left[ \sum_{t=0}^T \gamma^t r_t \right]$ 。
梯度公式：
$\nabla_\theta J(\theta) = \mathbb{E}_{s \sim \rho^\pi, a \sim \pi(\cdot|s)} \left[ \nabla_\theta \log \pi(a|s; \theta) \cdot Q^\pi(s,a) \right]$
物理意义：通过调整动作概率分布，增加高Q值动作的概率，随机策略梯度通过调整动作概率间接优化Q值，无需计算Q对动作的导数。

特点

探索机制：通过概率分布自然探索（如高熵策略）。
计算复杂度：需处理概率分布或采样动作（连续空间计算复杂）。
适用场景：离散或连续动作空间，需显式探索的任务（如多臂老虎机）。

代码理解

# 策略网络输出动作概率
  probs = policy_network(state)
  action_dist = Categorical(probs)
  action = action_dist.sample() # 随机策略需要采样，通过优化概率优化策略

  # 计算梯度
  log_prob = action_dist.log_prob(action)
  loss = -log_prob * Q_value  # Q_value为蒙特卡洛回报或Critic估计值
  loss.backward()

直接使用Q值作为权重，不涉及对Q的求导。

7.2. 确定性策略梯度（Deterministic Policy Gradient）

原理

策略形式：策略直接输出确定性动作，即 $\mu(s; \theta)$ 。
目标函数：最大化Q值 $Qμ(s,μ(s;θ))Q^\mu(s, \mu(s; \theta))$ 。
梯度公式：
$\nabla_\theta J(\theta) = \mathbb{E}_{s \sim \rho^\mu} \left[ \nabla_\theta \mu(s; \theta) \cdot \nabla_a Q^\mu(s,a) \big|_{a=\mu(s)} \right]$
物理意义：直接调整动作 ( a ) 的方向以最大化Q值，需知道Q值对动作的敏感度。确定性策略梯度直接优化动作值以最大化Q值，必须计算Q对动作的导数并通过链式法则更新策略参数。

代码理解：

    actor_target = Actor(state_dim, action_dim, max_action)
    actor_optimizer = optim.Adam(actor.parameters(), lr=1e-4)

    # 策略网络输出确定性动作
    deterministic_action = actor_network(state) # 不需要采样
    # Critic网络评估Q值
    q_value = critic_network(state, deterministic_action)

    # 计算梯度(需Q对动作的导数),通过优化Q值梯(变大的方向)直接优化action
    actor_loss = -q_value.mean()  # 最大化Q值
    acto_optimizer.zero_grad()
    actor_loss.backward()
    acto_optimizer.step()

Critic计算 $∇aQ(s,a)\nabla_aQ(s,a)$ 反向传播至Actor网络, actor_optimizer只有actor模型的parameters，critic损失的反响传播会把 $∇aQ(s,a)\nabla_aQ(s,a)$ 梯度传播到actor，但是critic模型的参数不会被actor_optimizer优化。

特点

探索机制：需依赖外部噪声（如OU噪声或高斯噪声）。
计算复杂度：直接优化动作值，无需概率积分（高效）。
适用场景：连续动作空间的高效优化（如机器人控制）。

7.3. 核心区别

特性	随机策略梯度	确定性策略梯度
策略输出	动作概率分布 $π(a∥s;θ)\pi(a\\|s;\theta)$	确定性动作 $\mu(s; \theta)$
梯度计算	依赖 $∇θlog⁡π(a∥s)\nabla_\theta \log \pi(a\\|s)$	依赖 $∇aQ(s,a)\nabla_a Q(s,a)$ 和 $∇θμ(s)\nabla_\theta \mu(s)$
探索方式	通过概率分布自然探索	需外部添加噪声
优化目标	增加高Q值动作的概率	直接优化动作以最大化Q值
计算效率	高维连续空间计算复杂（需采样）	高效（无概率积分或采样）
典型算法	REINFORCE, A2C, PPO	DDPG, TD3