算法设计与分析实验：强连通分量与图遍历

  

目录

一、查找集群内的关键连接

1.1 思路一：DFS

1.2 思路二：BFS

二、The Cow Prom S

2.1 具体思路

2.2 流程展示

2.3 代码实现

2.4 代码复杂度分析

2.5 运行结果

结尾语

---

一、查找集群内的关键连接

力扣第1192题

连通分量算法通常使用深度优先搜索（DFS）和广度优先搜索（BFS）实现。本题，我们首先使用DFS来找到关键连接。

1.1 思路一：DFS

（1）具体思路

将connections中的边存储为邻接表形式。我们首先需要把输入的边列表转换为邻接表表示，以便于我们进行深度优先搜索。

访问每个节点，从任意一个节点开始进行深度优先搜索，记录每个节点被遍历的时间戳，并记录当前最小的时间戳low。因为对于每个节点，我们都要从任意一个节点开始进行深度优先搜索。我们使用一个计数器i来记录每个节点被访问的时间戳，即ids[node] = i。同时，我们也需要记录当前最小的时间戳low，初始值为ids[node]。

如果发现某个节点v的子节点u的low值小于v的时间戳，则说明这是一条关键连接

在进行深度优先搜索的过程中，对于每一个节点v，我们需要遍历它的所有相邻节点，并判断它是否是关键连接。

如果发现某个节点v的子节点u的low值小于v的时间戳，则说明u不能通过其他路径到达v，因此(u, v)就是一条关键连接。这是由于low值表示一个节点能够访问到的最小时间戳，如果一个节点的low值小于它的父节点的时间戳，说明该节点只能通过这条边到达父节点，删除该边会导致该节点无法连接父节点及其它子节点。

重复步骤2和3直到所有节点都被遍历过。

最后，返回存储了所有关键连接的列表res。

（2）流程展示

以下是一个示例图，展示了一个包含6个节点和7条边的图，并用DFS的方式遍历该图寻找关键连接：

对于这个示例图，我们首先将边列表转换为邻接表形式：

connections = [[0, 1], [1, 2], [2, 0], [1, 3], [3, 4], [4, 1], [2, 5]]

对应的邻接表如下：

graph = {

    0: [1, 2],

    1: [0, 2, 3, 4],

    2: [0, 1, 5],

    3: [1, 4],

    4: [3, 1],

    5: [2]

}

假设我们从节点0开始进行深度优先搜索，初始时间戳为1，low值也为1。我们从0开始遍历其相邻节点1和2，此时它们的时间戳都为2，low值也为2。接着我们遍历节点1的相邻节点2、3和4，此时它们的时间戳分别为3、4和5，而它们的low值分别为2、3和2。其中，节点2的low值小于节点1的时间戳，因此边(1, 2)是一条关键连接。接着我们遍历节点2的相邻节点0和5，此时它们的时间戳分别为6和7，low值也分别为2和2。因为节点2没有其它相邻节点了，所以我们返回到节点1，并继续遍历它的相邻节点，即节点3和4。此时节点3的low值小于节点1的时间戳，因此边(1, 3)是一条关键连接。

接着我们遍历节点4的相邻节点1和3，此时它们的时间戳分别为8和9，而它们的low值分别为4和4。因为节点4没有其它相邻节点了，所以我们返回到节点3，并继续遍历其相邻节点4。此时我们发现节点4和节点1之间的边(1, 4)也是一条关键连接。最后，我们遍历节点5的相邻节点2，此时它们的时间戳都为10，low值也为10。因为节点5没有其它相邻节点了，所以遍历结束。

（3）代码实现

from collections import defaultdict
from typing import List


class Solution:
    def criticalConnections(self, n: int, connections: List[List[int]]) -> List[List[int]]:
        graph = defaultdict(list)  # 建立邻接表
        for conn in connections:
            graph[conn[0]].append(conn[1])
            graph[conn[1]].append(conn[0])

        ids = [-1] * n  # 记录每个节点被访问的时间戳
        lows = [-1] * n  # 记录当前最小的时间戳
        res = []  # 存储关键连接

        def dfs(node, parent, i):
            ids[node] = i
            lows[node] = i
            i += 1
            for neighbor in graph[node]:
                if ids[neighbor] == -1:  # 如果该节点未被访问
                    i = dfs(neighbor, node, i)
                    lows[node] = min(lows[node], lows[neighbor])  # 更新当前最小的时间戳

                    if lows[neighbor] > ids[node]:  # 该节点子节点的low值小于该节点的时间戳，这是一条关键连接
                        res.append([neighbor, node])
                elif neighbor != parent:  # 如果该节点已经被访问，但不是父节点
                    lows[node] = min(lows[node], ids[neighbor])  # 更新当前最小的时间戳
            return i

        dfs(0, -1, 0)  # 从节点0开始进行深度优先搜索

        return res


# 测试部分
solution = Solution()
n = 4
connections = [[0, 1], [1, 2], [2, 0], [1, 3]]
output = solution.criticalConnections(n, connections)
print(output)  # 预期输出: [[1, 3]]

n = 2
connections = [[0, 1]]
output = solution.criticalConnections(n, connections)
print(output)  # 预期输出: [[0, 1]]

（4）代码复杂度分析

在 DFS 中，我们遍历了图中的每个节点，并对每个节点进行以下操作：

设置节点的 ids 和 lows 数组，时间复杂度为 O(1)。

遍历节点的每个邻居，并递归调用 DFS，时间复杂度为 O(n)，其中 n 是节点的邻居数。

更新节点的 lows 数组，时间复杂度为 O(1)。

因此，DFS 的时间复杂度可以表示为：T(n) = O(n) + Σ(T(v))，其中 T(v) 表示节点 v 的 DFS 时间复杂度。

接下来分析整个算法的时间复杂度。

建立邻接表：对于每条边，需要将其添加到邻接表中，时间复杂度为 O(E)，其中 E 是边的数量。

初始化数组和结果列表：需要遍历所有节点，时间复杂度为 O(n)。

执行 DFS：对于每个节点进行 DFS 操作，时间复杂度为 Σ(T(v))，其中 v 表示节点。

总体时间复杂度：O(E + n + Σ(T(v)))

另外，空间复杂度主要取决于邻接表和节点数组的空间占用，即 O(E + n)。

综上所述，该代码的时间复杂度为 O(E + n + Σ(T(v)))，空间复杂度为 O(E + n)。其中 E 表示边的数量，n 表示节点的数量，T(v) 表示节点 v 的 DFS 时间复杂度。

1.2 思路二：BFS

（1）具体思路

利用队列这个数据结构。首先将connections中的边存储为邻接表形式。

创建一个队列，并将任意一个节点入队。

对于每个节点v，维护一个visited列表来记录该节点是否被访问过。

在循环中，从队列中取出一个节点v，并标记为已访问。

遍历节点v的相邻节点u，如果节点u未被访问过，则将u入队，并将(u, v)加入关键连接列表。

重复步骤4和5直到队列为空。

（2）流程展示

connections = [[0, 1], [1, 2], [2, 0], [1, 3]]

节点编号： 0   1   2   3

初始状态：

visited: [False, False, False, False]

关键连接: []

开始进行BFS遍历：

队列: [0]

I. 出队节点 0，标记为已访问

visited: [True, False, False, False]

关键连接: []

II. 遍历节点 0 的相邻节点：

    - 相邻节点 1 未访问过，入队，并将 (0, 1) 加入关键连接列表

    队列: [1]

    visited: [True, True, False, False]

    关键连接: [(0, 1)]

III. 遍历节点 1 的相邻节点：

    - 相邻节点 2 未访问过，入队，并将 (1, 2) 加入关键连接列表

    队列: [2]

    visited: [True, True, True, False]

    关键连接: [(0, 1), (1, 2)]

    

IV. 遍历节点 2 的相邻节点：

    - 相邻节点 0 已访问过，跳过

    队列: []

    visited: [True, True, True, False]

    关键连接: [(0, 1), (1, 2)]

遍历结束，关键连接列表为：[(0, 1), (1, 2)]

（3）代码实现

#BFS
from collections import defaultdict, deque

class Solution:
    def criticalConnections(self, n: int, connections: List[List[int]]) -> List[List[int]]:
        graph = defaultdict(list) #建立邻接表
        for conn in connections:
            graph[conn[0]].append(conn[1])
            graph[conn[1]].append(conn[0])
        
        visited = [False] * n #记录节点是否被访问过
        lows = [-1] * n #记录当前最小的时间戳
        res = [] #存储关键连接
        
        queue = deque()
        queue.append(0) #从节点0开始进行广度优先搜索
        visited[0] = True
        
        while queue:
            node = queue.popleft()
            for neighbor in graph[node]:
                if not visited[neighbor]:
                    queue.append(neighbor)
                    visited[neighbor] = True
                    lows[neighbor] = lows[node] + 1

                    if lows[neighbor] > lows[node]: #该节点的low值大于父节点，这是一条关键连接
                        res.append([neighbor, node])
        
        return res

（4）运行结果

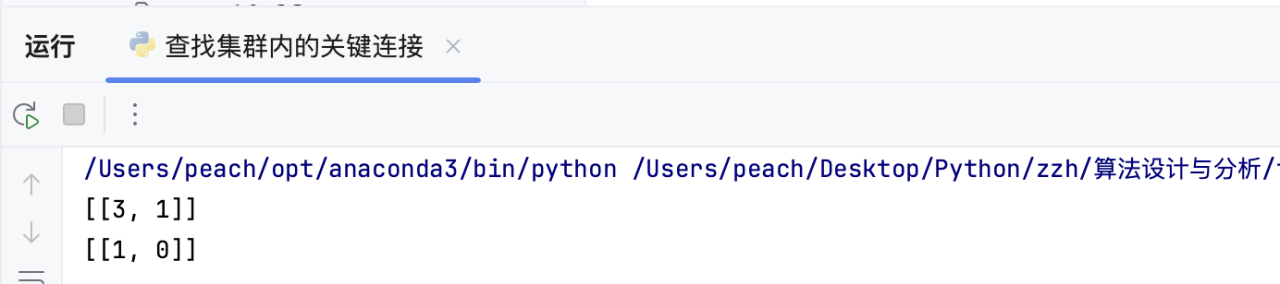
观察结果可知与预期结果一致

二、The Cow Prom S

P2863 [USACO06JAN]

本题使用 Kosaraju 算法进行求解。

2.1 具体思路

首先，Kosaraju 算法的基本思路是：

对原图进行一次深度优先遍历，得到每个节点的“结束时间”；

对原图进行一次反向操作（即将所有的边反向），按照结束时间从大到小的顺序对每个节点进行深度优先遍历，这些遍历所得到的集合就是该节点所在的强连通分量。

因此在具体实现时，可以按照如下步骤进行：

建立原图和反图的邻接表；

对原图进行一次深度优先遍历，记录每个节点的结束时间；

对反图按照结束时间从大到小的顺序进行深度优先遍历，记录遍历过程中所遇到的节点集合；

遍历记录的每个节点集合，若其包含多个节点，则说明存在一个点数大于1的强连通分量。

2.2 流程展示

假设我们有以下的有向图：

首先，我们需要建立原图和反图的邻接表。

原图的邻接表如下：

1: [2]

2: [3]

3: []

4: [5]

5: [2]

6: [1, 5]

反图的邻接表如下：

1: [6]

2: [1, 5]

3: [2]

4: []

5: [4, 6]

6: []

然后，我们对原图进行一次深度优先遍历，得到每个节点的结束时间。假设我们遍历的顺序是：3, 2, 1, 6, 5, 4。

接下来，按照结束时间从大到小的顺序对反图进行深度优先遍历，记录遍历过程中所遇到的节点集合。

首先从节点3开始深度优先遍历，得到的集合是：[3]。

然后从节点2开始深度优先遍历，得到的集合是：[2].

接着从节点1开始深度优先遍历，得到的集合是：[1, 6].

继续从节点6开始深度优先遍历，得到的集合是：[6].

再从节点5开始深度优先遍历，得到的集合是：[5].

最后从节点4开始深度优先遍历，得到的集合是：[4].

遍历完所有节点后，我们可以看到集合[1, 6]和集合[2]都包含多个节点，因此它们都是强连通分量。

2.3 代码实现

from collections import defaultdict

def kosaraju(n, edges):
    # 1. 建立原图和反图的邻接表
    graph = defaultdict(list)
    reverse_graph = defaultdict(list)
    for u, v in edges:
        graph[u].append(v)
        reverse_graph[v].append(u)

    # 2. 对原图进行一次深度优先遍历，得到每个节点的结束时间
    visited = set()
    timestamps = []
    def dfs(u):
        visited.add(u)
        for v in graph[u]:
            if v not in visited:
                dfs(v)
        timestamps.append(u)
    for u in range(1, n + 1):
        if u not in visited:
            dfs(u)

    # 3. 对反图按照结束时间从大到小的顺序进行深度优先遍历，记录遍历过程中所遇到的节点集合
    visited = set()
    sccs = []
    def reverse_dfs(u, scc):
        visited.add(u)
        scc.add(u)
        for v in reverse_graph[u]:
            if v not in visited:
                reverse_dfs(v, scc)
    while timestamps:
        u = timestamps.pop()
        if u not in visited:
            scc = set()
            reverse_dfs(u, scc)
            if len(scc) > 1:
                sccs.append(scc)

    # 4. 遍历记录的每个节点集合，若其包含多个节点，则说明存在一个点数大于1的强连通分量
    return len(sccs)

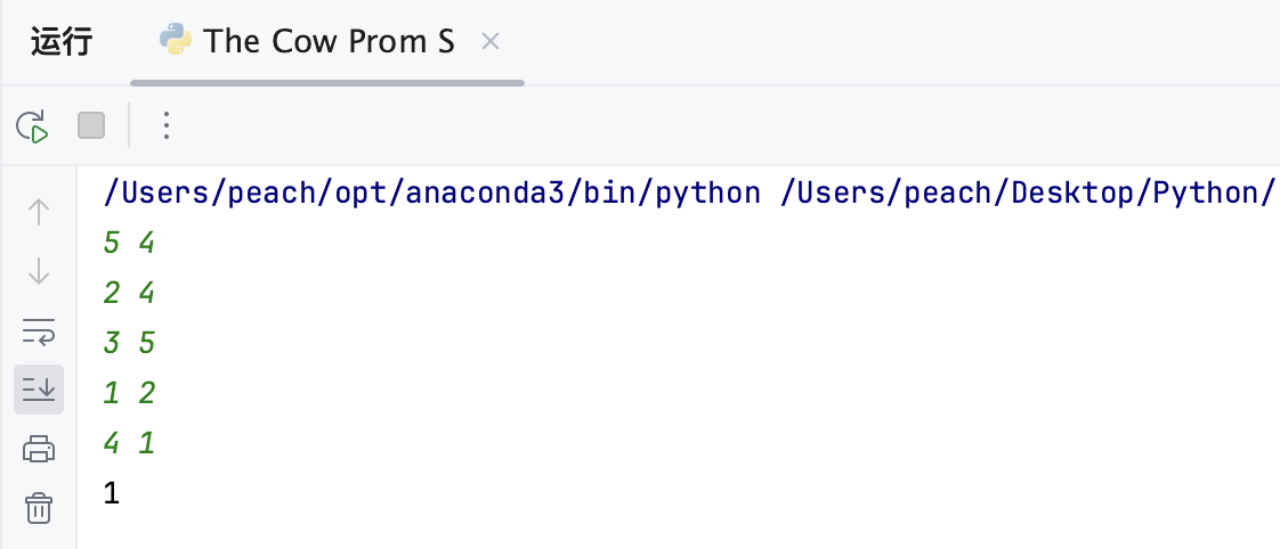
n, m = map(int, input().split())
edges = [list(map(int, input().split())) for _ in range(m)]
print(kosaraju(n, edges))

2.4 代码复杂度分析

建立原图和反图的邻接表：

时间复杂度：O(m)，其中 m 是边的数量。

对原图进行一次深度优先遍历，得到每个节点的结束时间：

时间复杂度：O(n + m)，其中 n 是节点的数量。

对反图按照结束时间从大到小的顺序进行深度优先遍历，记录遍历过程中所遇到的节点集合：

时间复杂度：O(n + m)

遍历记录的每个节点集合，若其包含多个节点，则说明存在一个点数大于1的强连通分量：

时间复杂度：O(num)，其中 num是强连通分量的数量。

综上，整个算法的时间复杂度为 O(n + m) + O(n + m) + O(num) = O(n + m + num)。

空间复杂度方面，主要用于存储图的邻接表、已访问节点的集合和强连通分量的列表。

图的邻接表所需空间：O(m)

已访问节点的集合所需空间：O(n)

强连通分量的列表所需空间：O(num) 

因此，整个算法的空间复杂度为 O(m + n + num)。

2.5 运行结果

结尾语

2024-2-1