实现图的宽度优先遍历

任务描述

本关任务：请你实现 graph.cpp 里的int Graph_WidthFirst(Graph*g, int start, Edge* tree)函数。 注意遵守约定：编号小的优先入队列。

相关知识

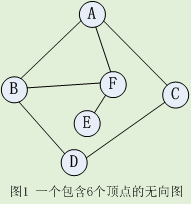
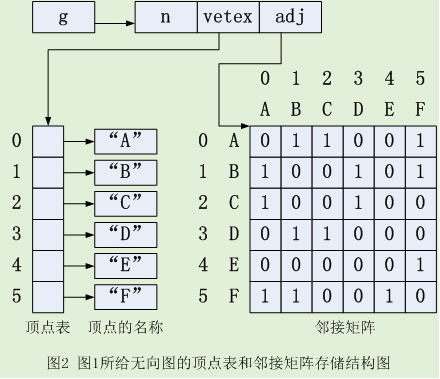
图 2 给出了对图 1 的无向图的存储结构图：每个顶点的名称由一个字符串描述，所有字符串的起始地址组织为一个数组，数组的起始地址为vetex；顶点的相邻关系保存在相邻矩阵中，其起始地址为adj，adj[i*n+j]的值为 1 表示i号顶点到j号顶点有边，为 0 表示无边，其中n是顶点个数，i和j是顶点在顶点表中的编号。 将n,vetex,adj组织成结构：

1. struct Graph {
2. int n;//顶点数
3. char** vetex;
4. int* adj;
5. };

给定指向该结构的指针g，就可以对图进行操作。

宽度优先遍历算法（伪代码）：

1. WidthFirst(Graph, start)
2. //输入Graph是图，start是开始顶点的编号
3. //输出：tree_edge[i]=<from,to>是遍历树的一条边
4. //tree_edge[1..n-1]为遍历树的n-1条边
5. //tree_edge[0].to … tree_edge[n-1].to是遍历序列
6. QueueIn(<-1,start>)
7. k=0;
8. while(QueueNotEmpty) {
9. <a,b>=QueueOut;
10. if (unvisited(b)) {
11. visit(b); // visit b, and set a flag for b.
12. tree_edge[k++]=<a,b>; // add <a,b> to the tree
13. for each <b,c> in the Edge Set {
14. if (unvisited(c)) QueueIn(<b,c>); //约定：编号小的先入队列
15. }
16. }
17. }

对图1运行该算法的结果： 生成树的边是：<-1,A> <A,B> <A,C> <A,F> <B,D> <F,E>； 宽度优先遍历的顶点访问次序是：A B C F D E。

编程要求

请你实现graph.cpp里的int Graph_WidthFirst(Graph*g, int start, Edge* tree)函数。 注意遵守约定：编号小的优先入队列。

1. //Graph.cpp
2. ///////////////////////////////////////////////////
3. #include <stdio.h>
4. #include <stdlib.h>
5. #include <string.h>
6. #include "Graph.h"
7. //////////////////////////////////////////////////
9. Graph* Graph_Create(int n)
10. {
11. Graph* g=(Graph*)malloc(sizeof(Graph));
12. g->n=n;
13. g->vetex=(char**)malloc(sizeof(char*)*n);
14. int i;
15. for (i=0; i<n; i++) g->vetex[i] = NULL;
16. g->adj=(int*)malloc(sizeof(int)*n*n);
17. int j;
18. for(i=0; i<n; i++) {
19. for(j=0; j<n; j++) {
20. g->adj[i*n+j]=0;
21. }
22. }
23. return g;
24. }
26. void Graph_Free(Graph* g)
27. {
28. free(g->adj);
29. int i;
30. for (i=0; i<g->n; i++) free(g->vetex[i]);
31. free(g->vetex);
32. free(g);
33. }
35. int Graph_WidthFirst(Graph*g, int start, Edge* tree)
36. //从start号顶点出发宽度优先遍历，（编号从0开始）
37. //返回访问到的顶点数，
38. //tree[]输出遍历树
39. //返回的tree[0]是(-1, start),
40. //真正的遍历树保存在tree[1..return-1], return是返回值
41. //顶点的访问次序依次为tree[0].to, tree[1].to, ..., tree[return-1].to
42. //输入时，tree[]的长度至少为顶点数
43. //返回值是从start出发访问到的顶点数
44. {
45. const int MAX=1000;
46. Edge queue[MAX];
47. int head=0, tail=0;
48. #define In__(a,b) {queue[tail].from=a; queue[tail].to=b; tail=(tail+1)%MAX;}/////////
49. #define Out__(a,b) {a=queue[head].from; b=queue[head].to; head=(head+1)%MAX;}//
50. #define QueueNotEmpty (head!=tail?1:0)///////////////////////////////////
51. #define HasEdge(i,j) (g->adj[(i)*g->n+(j)]==1)
53. char* visited=(char*)malloc(sizeof(char)*g->n);
54. memset(visited, 0, sizeof(char)*g->n);
56. int parent=-1;
57. int curr=start;
58. In__(parent, curr);
59. int k=0; //已经访问的结点数
61. //在begin和end之间实现你的代码
62. /*****Begin*****/
64. /*****End*****/
66. free(visited);
67. return k;
68. #undef In__//////////////////////////////
69. #undef Out__///////////////////////////////
70. #undef QueueNotEmpty////////////////////////
71. #undef HasEdge
72. }

测试说明

本关的测试过程如下：

1. 平台编译 step1/Main.cpp ；
2. 平台运行该可执行文件，并以标准输入方式提供测试输入；
3. 平台获取该可执行文件的输出，然后将其与预期输出对比，如果一致则测试通过；否则测试失败。

输入输出格式说明：

输入格式： 输入n，顶点数； 输入n个字符串，即n个顶点的名称，其编号按输入次序是,0,...,n-1； 输入若干数字对(a b)或<a b>，(a b)表示无向边，<a b>表示有向边； 输入字符x，表示边输入结束； 输入一个数start，表示开始顶点的编号。

输出格式： 输出生成树的边序列，边的第start个顶点构成的序列应是顶点访问序列。

以下是平台对 step1/Main.cpp 的测试样例： 样例输入

1. 6
2. A
3. B
4. C
5. D
6. E
7. F
8. ( 0 1 )
9. ( 0 2 )
10. ( 0 5 )
11. ( 1 3 )
12. ( 1 5 )
13. ( 2 3 )
14. ( 4 5 )
15. x
16. 0

样例输出

1. tree edges: <-1,A> <A,B> <A,C> <A,F> <B,D> <F,E>
2. visit sequence: A B C F D E

---

//Graph
///////////////////////////////////////////////////////////
#include <stdio.h>
#include <stdlib.h>
#include <string.h>
#include "Graph.h"
/////////////////////////////////////////////////////////////

Graph* Graph_Create(int n)
{
	Graph* g=(Graph*)malloc(sizeof(Graph));
	g->n=n;
	g->vetex=(char**)malloc(sizeof(char*)*n);
	int i;
	for (i=0; i<n; i++) g->vetex[i] = NULL;
	g->adj=(int*)malloc(sizeof(int)*n*n);
	int j;
	for(i=0; i<n; i++) {
		for(j=0; j<n; j++) {
			g->adj[i*n+j]=0;
		}
	}
	return g;
}

void Graph_Free(Graph* g)
{
	free(g->adj);
	int i;
	for (i=0; i<g->n; i++) free(g->vetex[i]);
	free(g->vetex);
	free(g);
}

int Graph_WidthFirst(Graph*g, int start, Edge* tree)
//从start号顶点出发宽度优先遍历，（编号从0开始）
//返回访问到的顶点数，
//tree[]输出遍历树
//返回的tree[0]是(-1, start), 
//真正的遍历树保存在tree[1..return-1], return是返回值
//顶点的访问次序依次为tree[0].to, tree[1].to,  ..., tree[return-1].to
//输入时，tree[]的长度至少为顶点数
//返回值是从start出发访问到的顶点数
{
	const int MAX=1000;
	Edge queue[MAX];
	int head=0, tail=0;
#define In__(a,b)  {queue[tail].from=a; queue[tail].to=b; tail=(tail+1)%MAX;}/////////
#define Out__(a,b)  {a=queue[head].from; b=queue[head].to; head=(head+1)%MAX;}//
#define QueueNotEmpty (head!=tail?1:0)///////////////////////////////////
#define HasEdge(i,j)  (g->adj[(i)*g->n+(j)]==1)

	char* visited=(char*)malloc(sizeof(char)*g->n);
	memset(visited, 0, sizeof(char)*g->n);

	int parent=-1;  
	int curr=start;
	In__(parent, curr); 
	int k=0; //已经访问的结点数
	/*请在BEGIN和END之间实现你的代码*/
    /*****BEGIN*****/
    while(QueueNotEmpty){
        Out__(parent,curr);
        if((HasEdge(parent,curr)||parent==-1)&&visited[curr]!=1){
            visited[curr]=1;
            tree[k].from=parent;
            tree[k].to=curr;
            k++;
            for(int i=0;i<g->n;i++)
            {
                if(HasEdge(curr,i)&&visited[i]!=1)
            {
                In__(curr,i)
            }
            }
        }
    }
    
    /*****END*******/
	return k;
#undef In__//////////////////////////////
#undef Out__///////////////////////////////
#undef QueueNotEmpty////////////////////////
#undef HasEdge
}