【模式识别】 概率密度函数的估计

引言

1，先验概率的估计比较简单，通常只需根据大量样本计算出各类样本在其中所占的比例，或者根据对所研究问题的领域知识实现确定。

2，两步贝叶斯决策：通过训练样本估计概率密度函数，再用统计决策进行类别判断

3，在监督学习中，训练样本的类别是已知的，而且假定各类样本中只包含本类的信息，这在多数情况下是正确的。因此，我们要做的是利用同一类的样本来估计本类的类条件概率密度。

4，概率密度函数的估计方法分为两大类：参数估计与非参数估计。参数估计中，已知概率密度函数的形式，但其中部分或者全部参数未知，概率密度函数的估计问题就是用样本来估计这些参数。主要方法又有两类：最大似然估计和贝叶斯估计，两者在很多实际情况下结果接近，但从概念上它们的处理方法是不同的。非参数估计，就是概率密度函数的形式也未知，或者概率密度函数不符合目前研究的任何分布模型，因此不能仅仅估计几个参数，而是用样本把概率密度函数数值化地估计出来。

5，在数理统计中，用来判断估计好坏的常用标准是无偏性，有效性和一致性。显然，无偏性，有效性都只是说明对于多次估计来说，估计量能以较小的方差平均地表示其真实值，并不能保证具体的一次估计的性能；而一致性则保证当样本数无穷多时，每一次的估计量都将在概率意义上任意地接近其真实值。

最大似然估计

一，最大似然估计的基本原理

1，假设

（1）要估计的参数是确定但未知的量，这与把它看作随机量的方法是不同的

（2）每类的样本满足独立同分布条件

（3）类条件概率密度具有某种确定的函数形式，只是其中的参数未知
（4）各类样本只包含本类的分布信息，也就是说，不同类别的参数是独立的，这样就可以分别对每一类单独处理。

2，基于上面的假设，可只考虑一类样本

3，基本思想

4，求解

（1）在似然函数满足连续可微的条件下

如果只有一个待估计参数

更一般地，多个未知参数组成的向量时，求解似然函数的最大值就需要对每一维分别求偏导

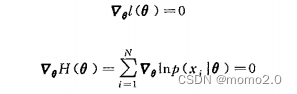
需要注意的是，在某些情况下，似然函数可能有多个极值，此时上述方程组可能有多个解，其中使得似然函数最大的那个解才是最大似然估计量。

（2）并不是所有概率密度形式都可以用上面的方法求得最大似然估计

二，正态分布下的最大似然估计

贝叶斯估计

一，基本思想

1，把参数估计看成贝叶斯决策问题，只是离散决策状态变成了连续空间里的决策

2，把带估计参数看成具有先验分布的随机变量，其取值和样本集有关，根据样本集估计参数

3，最优条件：最小错误率或最小风险

4，损失函数

5，贝叶斯决策和贝叶斯估计都立足于使贝叶斯风险最小，只是要解决的问题不同。前者是要决策x的真实状态，而后者则是估计样本集所属总体分布的参数

二，平方误差下贝叶斯估计的步骤

三，正态分布下的贝叶斯估计

1，求解

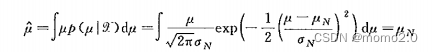
2，分析

正态分布下贝叶斯估计的结果是由两项组成的，一项是样本的算术平均，另一项是对均值的先验认识。当样本数目趋于无穷大时，第一项的系数趋于1而第二项的系数趋于0，即估计的均值就是样本的算术平均。这与最大似然估计是一致的。当样本数目有限时，如果先验知识非常确定，此时第一项的系数就很小，而第二项的系数接近1，估计主要由先验知识来决定。一般情况下，均值的贝叶斯估计是在样本算术平均与先验分布均值之间进行加权分布。

这里可以看到，贝叶斯估计的优势不但在于使用样本中提供的信息进行估计，而且能够很好地把关于待估计参数的先验知识融合起来，并且能够根据数据量大小和先验知识的确定程度来调和两部分信息的相对贡献。

概率密度估计的非参数方法

一，非参数估计的基本原理与直方图方法

1，直方图估计

2，非参数估计的基本原理

3，小舱选择

随样本数的增加，小舱体积应尽可能小，同时又必须保证小舱内有充分多样本，但每个小舱内的样本数又必须是总样本数中的很小的一部分。

我们自然可以想到，小舱内有多少样本不但与小舱体积有关，还与样本的分布有关。固定小舱宽度的直方图方法只是最简单的非参数估计方法，要想得到更好的估计，需要采用能够根据样本分布情况调整小舱体积的方法。

二，Kn近邻估计法

根据总样本确定一个参数kn，即在总样本数为N时我们要求每个小舱内拥有的样本个数。

这样，在样本密度比较高的区域小舱的体积就会比较小，而在密度低的区域则小舱体积自动增大

三，Parzen窗法

可以看作用核函数对样本在取值空间中进行插值

一个基本的要求是，这样估计出的函数至少应该满足概率密度函数的基本条件，即函数值应该非负且积分为1，显然这只需要

在这些窗函数中，都有一个表示窗口宽度的参数，也称作平滑参数，它反映了一个样本对多大范围内的密度估计产生影响。

当被估计的密度函数连续时，在核函数及其参数满足一定的条件下，parzen窗估计是逐渐无偏和平方误差一致的。这些条件是：对称且满足密度函数条件，有界，核函数取值随着距离的减小而迅速减小，对应小舱的体积应随着样本数的增加而趋于零，但是不能缩减速度太快，即慢于1/N趋于零的速度。

三，小结

作为非参数方法的共同问题是对样本数目需求较大，只要样本数目足够大，总可以保证收敛于任何复杂的未知密度，但是计算量和存储量都比较大。当样本数很少时，如果能够对密度函数有先验认识，则参数估计方法能取得更好的估计效果。

代码实战

问题描述：

已知四组一维数据集，样本数分别为16、256、1000和2000，请分别使用近邻估计法和Parzen窗法估计四组数据集的概率密度函数：

import numpy as np
import matplotlib.pyplot as plt
import pandas as pd


"""导入数据"""
df16 = pd.read_excel('./data/sampled_data_16.xlsx')
df256 = pd.read_excel('./data/sampled_data_256.xlsx')
df1000 = pd.read_excel('./data/sampled_data_1000.xlsx')
df2000 = pd.read_excel('./data/sampled_data_2000.xlsx')
data16 = df16.values    # (15, 1)
data256 = df256.values      # (255, 1)
data1000 = df1000.values    # (999, 1)
data2000 = df2000.values    # (1999, 1)

"""K近邻估计法"""
# 定义距离算法，此处采用欧氏距离
def Distance(x1, x2):
    return np.linalg.norm(x1-x2)
# 估算
def Density_cal(xx, data, kn):
    distances = np.array([Distance(xx, i) for i in data])
    # 得到最近的k个点中的最远的点距离索引
    dis_idx = np.argsort(distances)[kn-1]
    dis = distances[dis_idx]
    density = kn / (2*dis) / len(data)
    return density

"""Parzen窗法"""
# 高斯窗
def gaussian_pdf(xx, mu, sigma):
    pro = 1/np.sqrt(2*np.pi)/sigma*np.exp(-(xx-mu)**2/2/sigma**2)
    return pro
# 方窗
def square_pdf(xx, d, h):
    temp = abs(xx-d)/h
    comp = [0.5] * len(temp)
    ll = np.vstack((temp, comp))
    pro = np.argmax(ll, axis=0)/h
    return pro
# 计算概率密度
def parzen_window_pdf(xx, data, param, f):
    if f == 0:
        px = [gaussian_pdf(xx, mu, param) for mu in data]
    else:
        px = [square_pdf(xx, d, param) for d in data]
    return np.mean(np.array(px), axis=0)


"""估算概率密度并绘图"""

"""生成横坐标"""
# 选取数据集
# Data = data16
# Data = data256
# Data = data1000
Data = data2000
x = np.arange(min(Data)-1, max(Data)+1, 0.1)

"""K近邻估计法"""
# 对于不同数据集使用不同k值，以下为经测试我认为最合适的k值
# k = 4  # data16
# k = 16    # data256
# k = 100      # data1000
k = 200     # data2000
prob = [Density_cal(i, Data, k) for i in x]
plt.figure(figsize=(15, 10))
plt.plot(x, prob)
plt.plot(Data, [0]*len(Data), '.r')
plt.xlabel('x')
plt.ylabel('p(x)')
plt.title('K')
plt.grid()


"""Parzen窗法"""
# 最后参数为0的是高斯窗
prob01 = parzen_window_pdf(x, Data, 0.25, 0)
prob02 = parzen_window_pdf(x, Data, 1, 0)
prob03 = parzen_window_pdf(x, Data, 4, 0)
# 最后参数为1的是方窗
prob11 = parzen_window_pdf(x, Data, 0.25, 1)
prob12 = parzen_window_pdf(x, Data, 1, 1)
prob13 = parzen_window_pdf(x, Data, 4, 1)
# 绘图
plt.figure(figsize=(15, 10))
plt.subplot(231)
plt.plot(x, prob01)
plt.title("gaussian,0.25")
plt.plot(Data, [0]*len(Data), '.r')
plt.xlabel('x')
plt.ylabel('p(x)')
plt.subplot(232)
plt.plot(x, prob02)
plt.title("gaussian,1")
plt.plot(Data, [0]*len(Data), '.r')
plt.xlabel('x')
plt.ylabel('p(x)')
plt.subplot(233)
plt.plot(x, prob03)
plt.title("gaussian,4")
plt.plot(Data, [0]*len(Data), '.r')
plt.xlabel('x')
plt.ylabel('p(x)')
plt.subplot(234)
plt.plot(x, prob11)
plt.title("square,0.25")
plt.plot(Data, [0]*len(Data), '.r')
plt.xlabel('x')
plt.ylabel('p(x)')
plt.subplot(235)
plt.plot(x, prob12)
plt.title("square,1")
plt.plot(Data, [0]*len(Data), '.r')
plt.xlabel('x')
plt.ylabel('p(x)')
plt.subplot(236)
plt.plot(x, prob13)
plt.title("square,4")
plt.plot(Data, [0]*len(Data), '.r')
plt.xlabel('x')
plt.ylabel('p(x)')
plt.grid()
plt.show()

不同的h值代表了窗宽（或者带宽）的大小，它会影响概率密度估计的平滑程度。较小的h值会导致估计的概率密度函数更加尖锐和噪声敏感，反之，较大的h值会导致估计的概率密度函数更加平滑。

观察图形可以得到以下结论：

h值越小，概率密度估计曲线越尖锐，更能反映原始数据的细节特征，但容易受到噪声的影响。

h值越大，概率密度估计曲线越平滑，更能反映数据的整体分布情况，但可能会丢失一些细节特征