【LeetCode力扣】70. 爬楼梯 (简单)

最新推荐文章于 2025-04-09 12:13:48 发布

爱学的小涛

最新推荐文章于 2025-04-09 12:13:48 发布

阅读量1.1k

点赞数 20

文章标签： leetcode 算法 c语言学习

本文链接：https://blog.csdn.net/m0_65277261/article/details/134033485

版权

1、题目介绍

原题链接：70. 爬楼梯 - 力扣（LeetCode）

示例 1：

输入：n = 2
输出：2
解释：有两种方法可以爬到楼顶。
1. 1 阶 + 1 阶
2. 2 阶

示例 2：

输入：n = 3
输出：3
解释：有三种方法可以爬到楼顶。
1. 1 阶 + 1 阶 + 1 阶
2. 1 阶 + 2 阶
3. 2 阶 + 1 阶

提示：

1 <= n <= 45

2、解题

2.1、解题思路

我们可以用F(n)来表示爬到第n个阶梯的总方案数，因为一次可以上1或2个阶梯，所以最后一步可能跨了1个台阶，也可能跨了2个台阶；意思就是最后一步可能是从第n-1个台阶跨到了第n个台阶，或者是从第n-2个台阶跨到了第n个台阶；

根据上面的分析，我们可以看出爬到第n个阶梯的方案可以分为两个大部分：（1）可以先用能达到第n-1个阶梯的总方案爬到第n-1个阶梯后，再跨一个阶梯达到第n个阶梯；这一大部分的方案总数就是能达到第n-1个阶梯的总方案，即F(n-1) （2）可以先用能达到第n-2个阶梯的总方案爬到第n-2个阶梯后，再跨两个阶梯达到第n个阶梯；这一大部分的方案总数就是能达到第n-2个阶梯的总方案，即F(n-2)

所以爬到第n个阶梯的总方案数：F(n) = F(n-1) + F(n-2)

2.2、图解说明

提示：在下图，中四角星代表一步；五角星代表两步；红色方框里为F(n-2)的总方案；蓝色方框里为F(n-1)的总方案

到第1阶梯有一个方案：一步

到第2阶梯有两个方案：一步+一步；两步

到第3阶梯有三个方案：F(1)里的方案各加两步 {一步+两步} + F(2)里的方案各加一步 {一步+一步+一步；两步+一步}

即F(3) = F(1) + F(2)

到第4阶梯有五个方案：F(2)里的方案各加两步 {一步+一步+两步；两步+两步} + F(3)里的方案各加一步 {一步+两步+一步；一步+一步+一步+一步；两步+一步+一步}

即F(4) = F(2) + F(3)

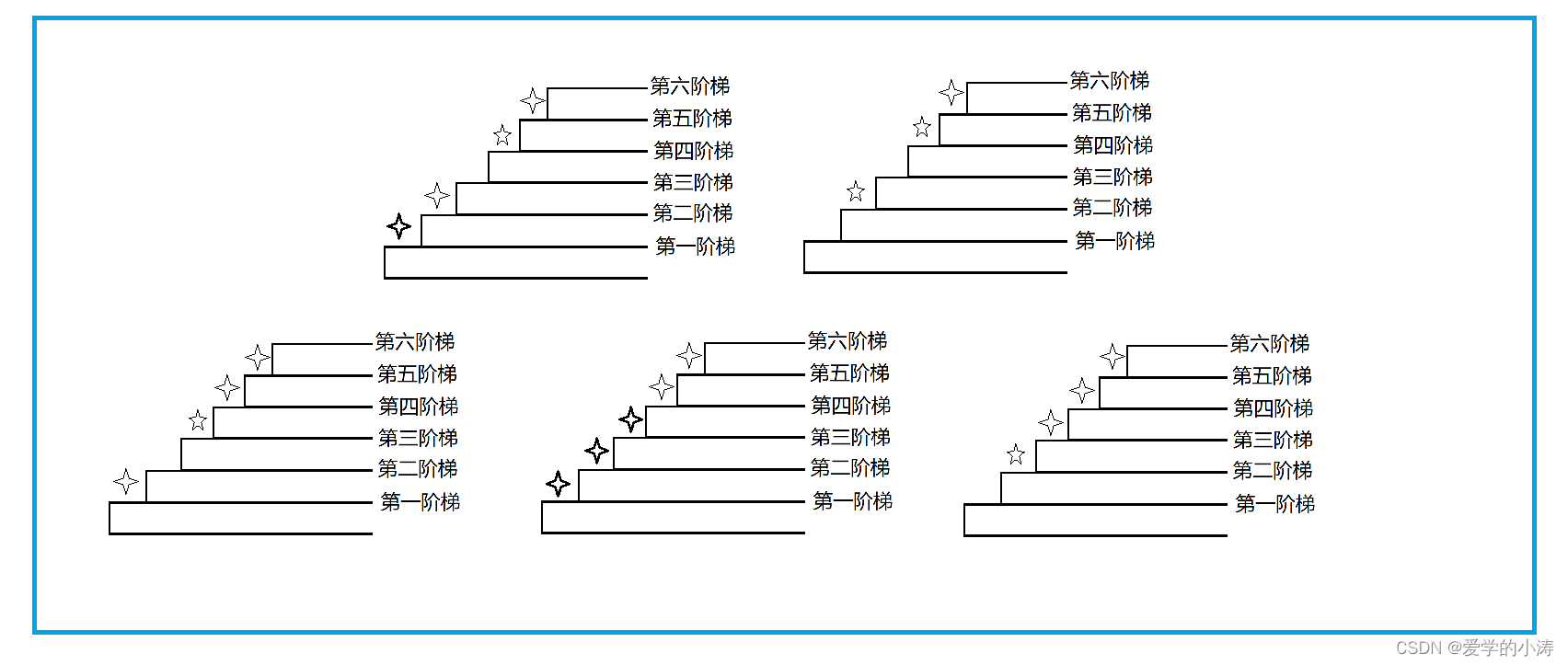
到第5阶梯有八个方案：F(3)里的方案各加两步 {一步+两步+两步；一步+一步+一步+两步；两步+一步+两步} + F(4)里的方案各加一步 {一步+一步+两步+一步；两步+两步+一步；一步+两步+一步+一步；一步+一步+一步+一步+一步；两步+一步+一步+一步}

即F(5) = F(3) + F(4)

2.3、解题代码

（1）滚动数组（用的是c语言）

int climbStairs(int n){
    int a = 0, b = 0, c = 1;
    for(int i = 1; i <= n; i++){
        a = b;
        b = c;
        c = a + b;
    }
    return c;
}

通过了

（2）递归（用的是c语言）

int sum(int n){
    if(n == 1){
        return 1;
    } else if(n == 2){
        return 2;
    }
    return sum(n-1)+sum(n-2);
}

int climbStairs(int n){
   return sum(n);
}

我们运行代码是可以解题的，但是这道题用递归这个方法会超时

【数据结构与算法】快速排序及其优化（随机划分值）-CSDN博客https://blog.csdn.net/m0_65277261/article/details/133959987?spm=1001.2014.3001.5502