【第二章 · 数字图像基础】

最新推荐文章于 2025-03-18 21:50:58 发布

不爱白开水

最新推荐文章于 2025-03-18 21:50:58 发布

阅读量4.1k

点赞数 24

分类专栏：数字图像处理学习笔记文章标签：图像处理笔记学习

本文链接：https://blog.csdn.net/m0_65547998/article/details/134695407

版权

数字图像处理学习笔记专栏收录该内容

3 篇文章

订阅专栏

第二章 · 数字图像基础

文章目录

第二章 · 数字图像基础
总结
视觉感知要素
- 亮度适应和鉴别
- - 两种现象清楚地表明感知亮度不是简单的强度的函数。
  - 视觉错觉（Optical Illusions）
光和电磁波谱
图像感知和获取
图像取样和量化
像素间的一些基本关系
基于像素的图像操作

总结

知识小点

图像的取样率——单位距离的取样数目（在两个空间方向上）
灰度级最大——白色；灰度级为0——黑色
注意数字图像处理坐标方向
x——箭头方向向下
y——箭头方向向右
灰度的取值范围为[0,L-1]；动态范围——也就是0~255有256个灰度级
RGB——R：红色；G：绿色；B：蓝色。
CMYK——C：青色；M：品红；Y：黄色；K：黑色。
HSI—— H：色调；S：饱和度；B：亮度。
空间分辨率：采样间隔——采样间隔值越小，空间分辨率越高
灰度分辨率：灰度值越低，图像分辨率越低，甚至出现假轮廓
邻域与邻接

图像存储大小计算

公式：b（需要比特数）=M（图像横坐标长度）*N（图像横坐标长度）*k（灰度级换算为以2为底的次数）
2的k次方等于灰度级

图像数学计算

加法：取反——灰度级最大值255-图像每个点灰度级
减法：增大差异——{（灰度级最大值255+[（图像每个点灰度级-灰度级最大值255）/2]}

图像逻辑计算

与
只要有0，结果就为0
任何值与0相与——结果为0
可以保留图像性质
或
只要有1，结果就为1
任何值与1相或——结果为1
在图像中提取图像
非
~1 =0
~0 =1

图像处理的空间操作

单象素操作；
邻域操作；
几何空间变换

视觉感知要素

本节主要介绍人眼的构造、成像等内容。

视觉的基本功能：空间辨别、时间辨别。
视知觉：颜色视觉、图形知觉、空间知觉

亮度适应和鉴别

人眼对不同亮度的适应和鉴别能力
亮 ——暗适应慢
暗 —— 亮适应快

两种现象清楚地表明感知亮度不是简单的强度的函数。

同时对比效应（Simultaneous Contrast）——背景变亮,相同强度的方块变暗。即人眼对某个区域感觉的亮度（主观亮度）不仅依赖于他自身的亮度，还与它的背景有关；
马赫带效应感觉亮度不是简单的强度函数的；视觉系统有趋于过高或过低估计不同亮度区域边界值的效应。图中各色带亮度恒定，但实际感觉条带边缘亮度有变化：边缘处，亮的一边更亮，暗的一边更暗；

视觉错觉（Optical Illusions）

在错觉中，眼睛填上了不存在的信息或错误地感知物体的几何特点。

请添加图片描述

光和电磁波谱

描述

电磁波谱可以用波长( λ )、频率( ν )或能量（ E ）来描述。
波长( λ )和频率( ν )的关系。
c=2.988*（10^8）–光速
波长单位是米（m）。常用的单位是微米（μm, 1μm=10^-6m；和纳米（nm,1nm=10^-9m
频率用赫兹（Hz）来度量，1Hz表示正弦波每秒1个周期。常用的能量单位是电子伏特。

请添加图片描述

电磁波谱的各个分量能量。h–普朗克常量

光 —— 可以被人眼感知的电磁波。

可见光谱是电磁波谱中相当窄的一部分。
电磁波是能量的一种，任何有能量的物体，都会释放电磁波。
人从物体感受的颜色由物体反射光决定
- 若所有反射的可见光波长均衡，则物体显示白色。
- 有颜色的物体是因为物体吸收了其他波长的大部分能量，从而反射某段波长范围的光。
- 没有颜色的光叫单色光或消色，灰度级通常用来描述单色光的强度，其范围从黑到灰，最后到白。
- 在原理上，如果可以开发出一种传感器，能够检测由一种电磁波谱发射的能量，就可以在那一段波长上对感兴趣的物体成像。

灰度和色彩

彩色模型：
RGB 加色法
CMY,CMYK 减色法
HSB(色泽,饱和度,明亮度)
灰度级—词通常用来表示单色光的强度。从黑到白的单色光的度量值范围通常称为灰度级，而单色图像常称为灰度图像。
色彩：彩色光的电磁能谱跨越0.43 um(紫色)~0.79 um(红色)的范围。
彩色光源的三个基本属性：
- ①发光强度——从光源流出的能量的总量。单位：瓦特(W)
- ②光通量——观察者从光源感受到的能量。单位：流明(lm)
  例如、从远红外光谱范围的光源发射出的光具有实际意义的能量，但观察者却很难感知到它。它的光通量几乎是零。
- ③亮度——光感受的主观描绘子。单位：不能测量
  它实际上不能度量。它具体体现了强度的无色概念,是描述彩色感觉的参数之一。

图像感知和获取

使用单个传感器获取图像

单个传感器通过运动来生成二维图像

图中显示了单个传感器的部件。也许最熟悉的这类传感器是光二极管，它由硅材料构成.并且其输出电压波形与入射光成正比。在传感器前面用一个滤光器改善选择性。例如，光传感器前面的绿色(通过)滤光器有利于彩色谱的绿波段光通过。因此，传感器输出的绿光比可见光谱中的其他分量要强。
使用单个传感器成像的另一个例子是将一个激光源和传感器放在一起。使用镜子来控制扫描模式的发射光束，并将反射的激光信号引导到传感器。

使用条带传感器获取图像

图
比单个传感器更常用的几何结构是由内嵌传感器形式组成的传感器带。
以圆环形方式安装的传感器带用于医学和工业成像，以得到三维物体的剖面(“切片”)图像，
注意
- 传感器的输出必须由重建算法处理，重建算法的目的是把感知数据转换为有意义的剖面图像。换句话说，图像不可能单靠传感器的运动直接得到;它们需要进一步的处理。由图像堆叠组成的三维数字物体是由物体与传感器环在相垂直方向的运动产生的。
基于CAT原理的其他成像模式包括核磁共振成像(MRI)和正电子发射断层(PET)成像。

使用传感器阵列获取图像

简单的数字图像成像模型

外界光（太阳光）——>被照射物体反射（散光）——>接收设备接收——形成模拟图像——>取样——>量化——>数字图像
注
- 我们感兴趣的各类图像都是由“照射”源和形成图像的“场景”元素对光能的反射或吸收相结合而产生的。
- 图像形成模型
  在特定坐标(x,y)处，通过传感器转换获得的f值为一正的标量。
- 函数f(x,y)可由两个分量表征：
  ①入射到观察场景的光源总量；i(x,y)入射分量。
  ②场景中物体反射光的总量组成；r(x,y)反射分量。
- 入射分量【i(x,y)】与反射分量【r(x,y)】
  - 两个函数乘积合并形成f(x,y)
    公式
    其中
    灰度（Intensity）
    
    白光强度（illumination）性质取决于照射源
    平均反射系数（reflectance）性质取决于成像物体的特性
    反射分量为零为全吸收；反射分量为为全吸收；

图像取样和量化

引言

获取图像的目标是从感知的数据中产生数字图像，但是传感器的输出是连续的电压波形，因此需要把连续的感知数据转换为数字形式。
转换也就是两种处理
取样：数字化坐标值。
量化：数字化幅度值。
图像的取样率：单位距离的取样数目（在两个空间方向上）

取样和量化的基本概念

概念

取样（数字化坐标值）——坐标的数字化称为采样；
量化（数字化幅度值）——幅度值的数字化为量化。

分类

均匀采样和量化
非均匀采样和量化

均匀采样和非均匀采样

图像的非均匀采样：

在灰度级变化尖锐的区域，用细腻的采样，在灰度级比较平滑的区域，用粗糙的采样。

图像的非均匀量化：

非均匀量化是依据一幅图像具体的灰度值分布的概率密度函数,按总的量化误差最小的原则来进行量化.

具体做法
- 对图像中像素灰度值频繁出现的灰度值范围,量化间隔取小一些,而对那些像素灰度值极少出现的范围,则量化间隔取大一些.
- 由于图像灰度值的概率分布函数因图像不同而异,所以不可能找到可用于所有图像的最佳非等间隔量化方法.

图像的数字化

黑白图像的数字化——用0、1表示颜色

0——黑
1——白

灰度图像的数字化——灰度0~255共256个灰度级；

灰度值为0——黑色
灰度值为255——白色

彩色图像的数字化（RGB）——红、绿、蓝

数字图象的表示

图像的表示方法

图像矩阵排列坐标图

一般，M、N和L取值为2的整数次幂。M,N必须为正数，L为灰度级,灰度的取值范围为[0，L-1]。
灰度级的取值范围一般称为图像的动态范围。

矩阵表达式

请添加图片描述
表达式的右侧定义了一幅数字图像。矩阵中的每个元素称为图像像素。

图像的坐标系的表示

（1）直角坐标系

请添加图片描述
1.坐标原点位于左下角
2.数据先沿x轴增加
3.然后沿y轴增加

（2）矩阵坐标系（MATLAB）

请添加图片描述
1.坐标原点位于左上角
2.数据先沿i轴增加
3.然后沿j轴增加
4.坐标值为整数

（3）像素坐标系（显示）

请添加图片描述
1、坐标原点位于左上角
2、数据先沿x轴增加
3、然后再沿y轴增加
4、坐标轴为整数

思考：

为什么图像经常用512×512、256×256、128×128等形式表述；

答: 因为当图像的大小是2的次幂时，图像的许多计算可以得到简化。

存储一幅512×512，有256个灰度级的图像需要多少比特？

答: 存储一幅大小为M×N，有2^k不同灰度级的图像所用的Bit数为: b=M×N×k 因此，存储一幅512×512 ，有256个灰度级（k=8）的图像需要512×512×8=2097152(Bit) 或 512×512=256K(Byte)
当M=N时，b=N²*k

空间和灰度分辨率

空间分辨率（spatial resolution）

直观上——空间分辨率是图像中可辨别的最小细节的度量。
数量上——有很多方法去说明，其中每单位距离线对数和每单位距离点数(像素数)是最通用的度量。
图像中可分辨的最小细节，主要由采样间隔值决定。（采样间隔值越小，空间分辨率越高）

灰度分辨率

灰度级别中可辨别的最小变化，通常也把灰度级L称为灰度分辨率

小结：

图像的分辨率表示的是能看到图像细节的多少，显然依赖于M×N和L
保持M×N不变而减少L则会导致假轮廓
保持L不变而减少M×N则会导致棋盘状效果
图像质量一般随着M×N和L的增加而增加，但存储量增大。

实验表明图像的细节越多，用保持M×N恒定而增加L的方法来提高图像的显示效果就越不明显，因此，对于有大量细节的图像只需要少数的灰度级。

图像的收缩与放大

（1）图像的收缩—— 行、列删除

（2）图像的放大

①创立新的象素位置；
②给新象素赋灰度值

双线性内插方法

定义
使用邻近4 个点的像元值,按照其距内插点的距离赋予不同的权重,进行线性内插
公式

双三次内插——复杂度较高

公式
双三次内插在保持细节方面比双线性内插相对要好。
双三次内插是商业图像编辑程序的标准内插方法，例如Adobe Photoshop和 CorelPhotopaint。

像素间的一些基本关系

假设——像素p(m,n)

相邻像素

p的4邻域——N₄p

p的4邻域像素坐标—— (m+1,n),(m-1,n),(m,n+1),(m,n-1)

p的对角相邻邻域 ——N_Dp

p的对角相邻邻域像素坐标——(m+1,n+1),(m+1,n-1),(m-1,n+1),(m-1,n-1)

p的8邻域——N₈p

p的8邻域像素坐标——N₄ p+ N_Dp
N4§ + ND§ = (m+1,n),(m-1,n),(m,n+1),(m,n-1)，(m+1,n+1),(m+1,n-1),(m-1,n+1),(m-1,n-1)

邻接性、连通性、区域和边界

邻接——像素的相邻仅说明了两个像素在位置上的关系，若再加上取值相同或相近，则称两个像素邻接。

两个像素p和q邻接的条件

（1）位置相邻
p(m,n)和q（s,t）位置上满足相邻，即
（2）灰度值相近
即称为灰度值相近（似）准则。称为灰度值相近（似）准则。

令V是用于定义邻接性的灰度值集合（相似性准则），存在三种类型的邻接性：

（1）4邻接:
若像素p和q的灰度值均属于V中的元素，且q在N₄p中，则p和q是4邻接的。
（2）8邻接:
若像素p和q的灰度值均属于V中的元素，且q在N₈p集中,则p和q是8邻接的。
（3）m邻接(混合邻接):
若像素p和q的灰度值均属于V中的元素，
{ ①q在N₄p中,或者
②q在N_Dp中}且{集合N₄p∩N₄q没有V值的像素},则具有V值的像素p和q是m邻接的。
4邻接与8邻接的关系 ——（4邻接必8邻接，反之不一定成立。）
两种邻接及其关系见下图所示，相似性准则为V={1}，p与q： 4邻接，也8邻接；q与r ：8邻接但非4邻接。
混合邻接是8邻接的改进。混合邻接的引入是为了消除采用8邻接时产生的（通路）二义性。
只定义8邻接，则q₂和q₁之间的通路有两条（二义）；
定义了m邻接，则q₂和q₁之间的通路就只有一条（m通路）

通路

像素p(x₀,y₀)到像素q(x_n,y_n)的通路(path)定义为特定的像素序列：(x₀,y₀),(x1,y1), (x₂,y₂) …,(xn,yn), st.(xi,yi)和(x_i-1,yi~-1)(对于1≤i≤n)是邻接的.
n是通路的长度.

连通性

若S是图像中的一个象素子集，对任意的p,q∈S，如果存在一条由S中像素组成的从p到q的通路，则称p在图像集S中与q连通，连通也分为4连通和8连通。
连通集：如果S中仅有一个连通分量，则S叫连通集；

区域(region)

区域：R是图像中的像素子集。如果R是连通集，则称R为一个区域（黄色部分）。
邻接区域：两个区域。如果联合（并）为一个区域，则称这两个区域为邻接区域。如图Ri和Rj
注意
①定义区域时，必须指明灰度相似性准则V={ }
灰度相似性准则V不一样，则区域就不一样；
②定义邻接区域时，还必须指明邻接类型；
（a）中，Ri和Rj是4邻接区域，且Ri＋Rj为连通集；
（b）中， Ri和Rj是8邻接区域，但Ri＋Rj为非连通集；

区域的边界(boundary)

内边界:一个区域的边缘或轮廓线叫做边界。（即：该区域中和其背景相邻接的点的集合）
外边界:对应于背景边界
一个区域和其背景中的点之间的邻接要根据8连通来定义！！！

距离度量

D是距离的度量函数。

对于像素点p(x,y),q(s,t),z(v,w),
（1）正定性
（2）对称性
（3）距离三角不等式
各像素点的距离计算方法
欧氏距离(类似三角形求边长)
D4距离（城市街区距离）
D8距离（棋盘距离）
欧式距离、D4距离、D8距离三种距离的关系为通过D4和D8的计算，可以大大减少运算量，以适应数字图像数据量很大的特点
Dm距离:
欧式距离、D4距离、D8距离和通路无关、只和点坐标有关
Dm距离用点间最短通路决定

基于像素的图像操作

阵列与矩阵操作(复习线性代数)

包含一幅或多幅图像的阵列操作是以逐像素为基础执行的。图像可以等价地被看成是矩阵。
当我们谈到一幅图像的求幂时，意味着每个像素均进行求幂操作；当我们谈到一幅图像除以另一幅图像时，意味着在相应的像素对之间进行相除。

线性和非线性操作

（1）线性算子H
请添加图片描述
输人乘以常数的线性操作的输出与乘以该常数的原始输入的操作的输出是相同的。第一个特性称为加性，第二个特性称为同质性。
（2）非线性算子：不满足上面公式的算子

图像处理的算术操作

定义

算数运算是指对两幅或多幅输入图像进行点对点的加、减、乘、除计算而得到输出图像的运算

注

算术运算只涉及一个空间位置（象素）的运算；
算术运算在相同大小的图像之间进行；
两幅图像的相除看成用一幅的取反图像与另一幅图像相乘.
图像的乘法不仅可以用于对二进码模板进行处理,而且可以直接用于灰度处理.
减法处理主要用于增强两幅图像的差异。

加法

公式
作用
一、去除“叠加性”噪音
二、生成图像的叠加效果

减法

减法的定义
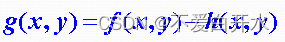
主要应用举例
去除不需要的叠加性图案；
检测两幅图像之间的差别；
计算物体边界的梯度（差分运算）；
去除不需要的叠加性图案,电视制作的蓝屏技术就基于此
检测两幅图像之间的差别，增强细节。图像减法处理:计算两幅图像对应像素点的差.。主要作用：增强两幅图像的差异。
检测同一场景两幅图像之间的变化
计算物体边界的梯度。在一个图像内，寻找边缘时，梯度幅度（描绘变化陡峭程度的量）的近似计算

乘法：

注：在MATLAB中要用点乘运算

乘法的定义

请添加图片描述

主要应用举例

图象的局部显示（用二值模板图像与原图像做乘法）

小结

给定一幅图像f，保证图像间算术操作的结果的整个值域落入某个固定bit数的方法如下：
（1）生成一幅灰度最小值为0的图像fm
（2）生成一幅灰度值在[0,K]范围内的图像fs：
例如：处理8bit图像时，K＝255
注意：执行除法时，需将一个较小的灰度值加到除数图像的像素上，以避免除数为0。

集合和逻辑操作

图像中的逻辑操作主要以像素对像素为基础在两幅或多幅图像间进行。

逻辑运算：与、非、或（象素灰度值作为二进制串处理）

基本集合操作

逻辑操作

在处理二值图像时，我们可以把图像想象为像素集合的前景(1值)与背景(0值)。
处理二值图像时，OR、AND和 NOT逻辑操作就是指普通的并、交和求补操作，在逻辑理论中，1代表真,0代表假。
考虑由前景像素组成的区域(集合)A和B。这两个集合的
OR(或)操作结果不是属于A，就是属于B，或者属于两者。
AND操作是共同属于A和B的元素的集合。
集合A 的NOT操作是不在A中的元素的集合。

模糊集合

空间操作

直接在给定图像的象素上执行；分为以下三大类：

（1）单象素操作

描述公式
s =T(z)
z - 原图像中象素的灰度值；
s - 处理后图像中象素的灰度值

（2）邻域操作

公式
邻域处理的局部平均：
S_xy — f(x,y)中以任意一点（x,y）为中心的一个淋雨坐标集

（3）几何空间变换和图像配准；

几何空间变换（橡皮模变换）要改变图像中象素间的空间关系。

几何变换的两个基本操作：

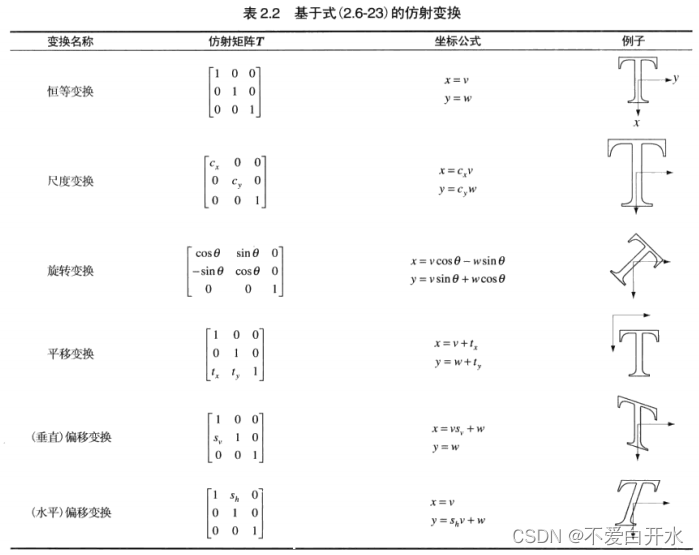
①坐标的空间变换；
代表式
(v,w)一原图像中象素的坐标;(x,y)一变换后图像中象素的坐标;
②灰度内插，即对空间变换后的像素赋灰度值。

基于例公式的

仿射变换
前向映射
- 它由扫描输人图像的像素，并在每个位置(v,w)
- 用式直接计算输出图像中相应像素的空间位置(x, y)组成。
- 不足：前向映射算法的一个问题是输人图像中的两个或更多个像素可被变换到输出图像中的同一位置，这就产生了如何把多个输出值合并到一个输出像素的问题。
  一种可能是某些输出位置可能完全没有要赋值的像素。
反向映射
- 扫描输出图像的象素(x,y)；
- 在每个位置(x,y)应用计算(v,w);
- 内插方法决定输出图像(x,y)处的灰度值；

向量与矩阵操作

多光谱图像处理是使用向量和矩阵操作的典型领域。大小为M×N的RGB彩色图像就可用这一大小的三个分量图像来表示，或者总共用MN个三维向量来表示。

图像变换

线性变换域中操作的一般方法
基本步骤
首先，变换输入图像，
然后用预定义的操作修改该变换，
最后，输出图像由计算修改后的变换的反变换得到。

图像处理的概率方法

概率方法应用的前提：直将图像的灰度值看成是随机变量
均值和方差对于图像的视觉特性有明显的直接关系，高阶距更敏感！
均值和方差对于图像的视觉特性有明显的直接关系，高阶矩更敏感。例如，一个正三阶矩指出其灰度倾向于比均值高，负三阶矩则指出相反的条件,并且零三阶矩告诉我们灰度近似相等地分布在均值的两侧。这些特性对于计算目的很有用，但它们一般不能告诉我们更多图像外观的内容。