图——邻接矩阵基本操作算法实现

原创 已于 2025-07-28 15:30:28 修改 · 278 阅读 · 0 ·
CC 4.0 BY-SA版权
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
文章标签：

#算法 #数据结构 #图论

于 2025-07-28 02:28:59 首次发布
部署运行你感兴趣的模型镜像

一、存储结构

#include <stdio.h>
#include <stdlib.h>
#define INFINT 9999999  //最大int值，即无穷
#define MAXVertexNum 100	//最大顶点数
 
typedef char VerTexType;	//顶点对应的数据类型 
typedef int ArcType;	//边对应的数据类型 

typedef struct{
	VerTexType vexs[MAXVertexNum];	//顶点表
	ArcType arcs[MAXVertexNum][MAXVertexNum];	//邻接矩阵,边表
	int vexnum,arcnum;	//图的当前点数和边数
	bool isUndirected; //记录是否为无向图 
}MGraph;

二、初始化操作

对顶点数和边数初始化为0

同时考虑顶点自身的边数为0

初始所有顶点之间没有变，设为无穷∞

void InitGraph(MGraph &G) {
    int i, j;

    // 设置图的当前顶点数和边数
    G.vexnum = 0;  // 初始化顶点数为0
    G.arcnum = 0;  // 初始化边数为0
	G.isUndirected = 1;   //默认为无向图 

    // 初始化邻接矩阵，将所有边的值设为INFINITY
    for (i = 0; i < MAXVertexNum; i++) {
        for (j = 0; j < MAXVertexNum; j++) {
            if (i == j) {
                G.arcs[i][j] = 0; // 顶点到自身的边为0
            } else {
                G.arcs[i][j] = INFINT;  // 无穷大表示没有边
            }
        }
    }
}

三、插入顶点操作

// 插入顶点函数
void InsertVertex(MGraph &G, VerTexType v) {
    if (G.vexnum >= MAXVertexNum) {
        printf("顶点表已满");
        return;
    }

    // 在顶点数组中插入新顶点
    G.vexs[G.vexnum] = v;
    G.vexnum++;
    return;
}

四、插入边操作

如果是无向图，则ij位置交替再赋值一次

if(G.isUndirected)  G.arcs[j][i] = weight; 

// 插入边函数
int AddEdge(MGraph &G, VerTexType v1, VerTexType v2, ArcType weight=1) {
    int i = -1, j = -1;

    // 查找顶点v1和v2在顶点表中的索引
    for (int k = 0; k < G.vexnum; k++) {
        if (G.vexs[k] == v1) {
            i = k;
        }
        if (G.vexs[k] == v2) {
            j = k;
        }
    }

    // 如果找到顶点v1和v2
    if (i != -1 && j != -1) {
        G.arcs[i][j] = weight;  // 插入边，v1 -> v2
        if(G.isUndirected)  G.arcs[j][i] = weight;  // 如果是无向图，插入边，v2 -> v1
        G.arcnum++;
        return 1; 
    } else {
        printf("顶点不存在");
        return 0;
    }
}

五、输出查看邻接矩阵

// 查看邻接矩阵的函数
void DisplayAdjMatrix(MGraph &G) {
    int i, j;

    // 打印顶点
    printf("顶点表");
    printf("   ");
    for (i = 0; i < G.vexnum; i++) {
        printf("%c ", G.vexs[i]);
    }
    printf("\n");

    // 打印邻接矩阵
    for (i = 0; i < G.vexnum; i++) {
        printf("%c: ", G.vexs[i]);
        for (j = 0; j < G.vexnum; j++) {
            if (G.arcs[i][j] == INFINT) {
                printf("INF ");
            } else {
                printf("%d ", G.arcs[i][j]);
            }
        }
        printf("\n");
    }
}

六、主函数

int main() {

//=====================================================
//无向图
//========
    MGraph G;  // 创建一个图
    InitGraph(G);  // 初始化图

    // 插入顶点
    InsertVertex(G, 'A');
    InsertVertex(G, 'B');
    InsertVertex(G, 'C');
    InsertVertex(G, 'D');
    InsertVertex(G, 'E');

    // 插入边
    InsertEdge(G, 'A', 'B');  
    InsertEdge(G, 'A', 'D');  
    InsertEdge(G, 'A', 'C');  
    InsertEdge(G, 'B', 'E');  
    InsertEdge(G, 'C', 'D');  
    DisplayAdjMatrix(G);
    return 0;
//=====================================================


}

 七、判断图是否存在边<x,y>或(y,x)

有向图和无向图算法一致

// 判断图是否存在边<x,y>或(y,x)
int Adjacent(MGraph G, VerTexType x, VerTexType y) {
    int i = -1, j = -1;
    
    // 查找顶点 x 和 y 的索引
    for (int k = 0; k < G.vexnum; k++) {
        if (G.vexs[k] == x) i = k;
        if (G.vexs[k] == y) j = k;
    }

    // 如果顶点存在并且存在边
    if (i != -1 && j != -1 && (G.arcs[i][j] != INFINT || G.arcs[j][i] != INFINT)) {
        return 1; // 存在边
    }
    return 0; // 不存在边
}

 八、列出图中节点 x 的邻接的边

考虑有向图的入边邻接点

// 列出图中节点 x 的邻接的边 
void Neighbors(MGraph G, VerTexType x) {
    int i = -1;

    // 查找顶点 x 的索引
    for (int k = 0; k < G.vexnum; k++) {
        if (G.vexs[k] == x) {
            i = k;
            break;
        }
    }

    if (i == -1) {
        printf("顶点 %c 不存在\n", x);
        return;
    }

    // 输出与顶点 x 相邻的所有顶点
    printf("顶点 %c 的邻接的边: ", x);
    for (int j = 0; j < G.vexnum; j++) {
        if (G.arcs[i][j] != INFINT && i != j) {
        	if(G.isUndirected==1) printf("(%c,%c) ", G.vexs[i],G.vexs[j]);
        	if(G.isUndirected==0) printf("<%c,%c> ", G.vexs[i],G.vexs[j]);
        }
        else (G.isUndirected==0 && G.arcs[j][i] != INFINT && i != j) { //考虑有向图的入边邻接点 
            printf("<%c,%c>", G.vexs[j],G.vexs[i]);
        }
    }
    printf("\n");
}

九、删除顶点操作

DeleteVertex(G,c) 在图中删除顶点x

有向图比无向图操作略有增加，主要体现在计算边数的时候

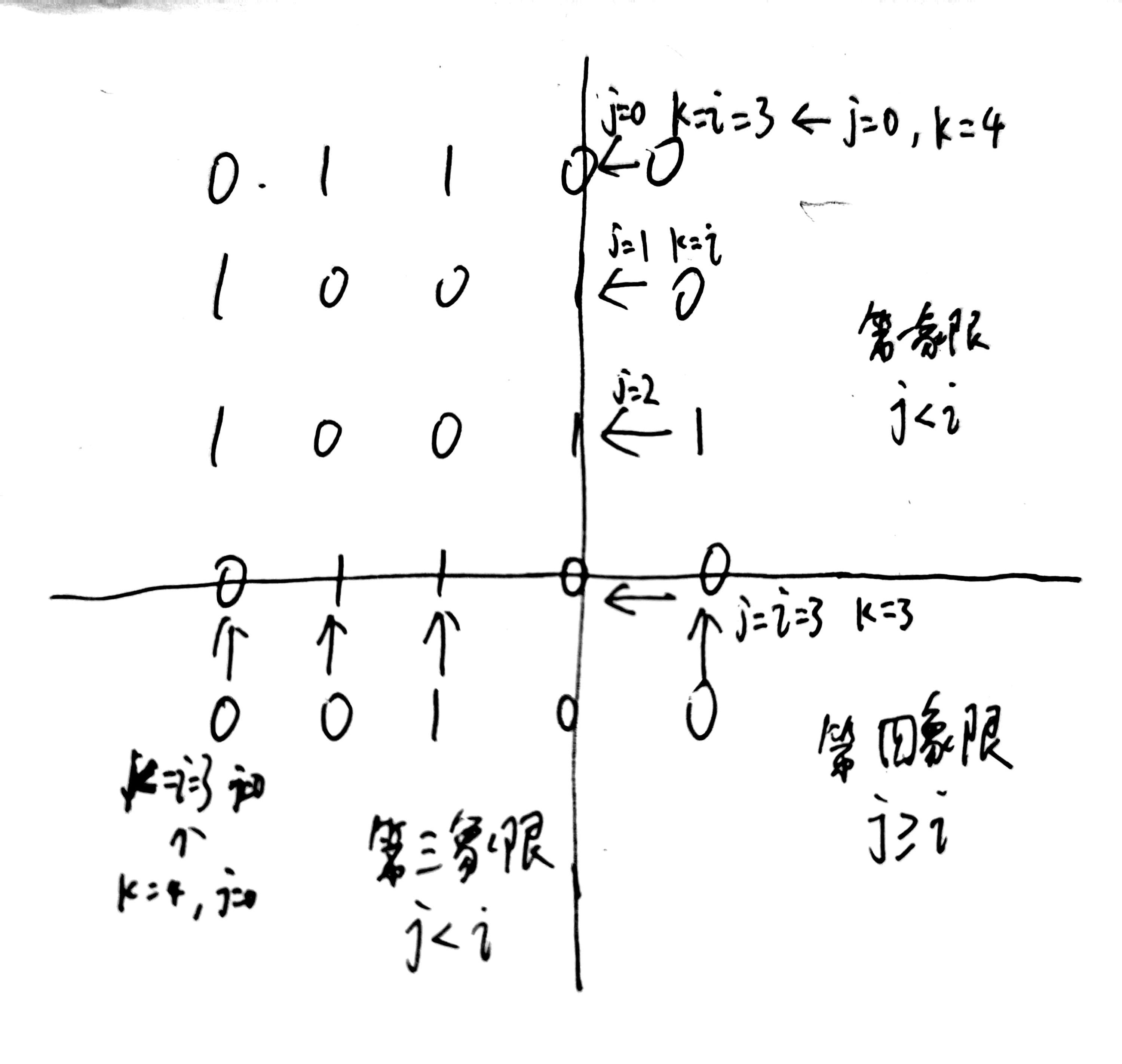
将图分成四块区域

按象限顺序，第二象限为不动组，

第一象限和第三象限为左移或上移一格组，

第四象限为先上移再左移组

操作示意图如下

// 删除顶点函数
void DeleteVertex(MGraph &G, VerTexType c) {
    int i, j;

    // 查找顶点 c 的索引
    for (i = 0; i < G.vexnum; i++) {
        if (G.vexs[i] == c) break;
    }

    if (i == G.vexnum) {
        printf("顶点 %c 不存在\n", c);
        return;
    }

    // 删除顶点 c 对应的行和列
    for (j = 0; j < G.vexnum - 1; j++) {
        G.vexs[j+i] = G.vexs[j + i + 1];
        for (int k = i; k < G.vexnum; k++) {
        	if(j<i) {
        		if(j<i && k==i && (G.arcs[j][k]!=INFINT && G.arcs[j][k]!=0)) G.arcnum--;
				
				// 如果是有向图，则需要判断双向         		
				if(G.isUndirected==0 &&j<i && k==i && (G.arcs[k][j]!=INFINT && G.arcs[k][j]!=0)) G.arcnum--;
        		
				G.arcs[j][k] = G.arcs[j][k+1];
        		G.arcs[k][j] = G.arcs[k+1][j];
			}
			if(j>=i){
				if(j==i && (G.arcs[j][k+1]!=INFINT && G.arcs[j][k+1]!=0)) G.arcnum--;
				
				//如果是有向图，则需要判断双向 
				if(G.isUndirected==0 && j==i && (G.arcs[k+1][j]!=INFINT && G.arcs[k+1][j]!=0)) G.arcnum--;
				if(G.isUndirected==0 && j==i && k==G.vexnum-1 && (G.arcs[k+1][j]!=INFINT && G.arcs[k+1][j]!=0)) G.arcnum--;
	            
				G.arcs[j][k+1] = G.arcs[j + 1][k+1];
	            G.arcs[j][k] = G.arcs[j][k+1];
	    	}
        }
    }

    G.vexnum--;
    
}

十、删除边操作

如果是无向图，则ij位置交替再删除一次，即删除两个方向的边

if(G.isUndirected)  G.arcs[j][i] = INFINT;

// 删除边函数
void RemoveEdge(MGraph &G, VerTexType x, VerTexType y) {
    int i = -1, j = -1;

    // 查找顶点 x 和 y 的索引
    for (int k = 0; k < G.vexnum; k++) {
        if (G.vexs[k] == x) i = k;
        if (G.vexs[k] == y) j = k;
    }

    if (i != -1 && j != -1) {
        G.arcs[i][j] = INFINT;
        if(G.isUndirected)  G.arcs[j][i] = INFINT; // 无向图需要删除两个方向的边
        G.arcnum--;
    } else {
        printf("边 (%c, %c) 不存在\n", x, y);
    }
}

 十一、求顶点 x 的第一个邻接点

求图中顶点x的第一个邻接点，若有则返回定点好，若x没有邻接点或图中不存在x，则返回-1

// 求顶点 x 的第一个邻接点
int FirstNeighbor(MGraph G, VerTexType x) {
    int i = -1;

    // 查找顶点 x 的索引
    for (int k = 0; k < G.vexnum; k++) {
        if (G.vexs[k] == x) {
            i = k;
            break;
        }
    }

    if (i == -1) {
        printf("顶点 %c 不存在\n", x);
        return -1;
    }

    // 查找第一个邻接点
    for (int j = 0; j < G.vexnum; j++) {
        if (G.arcs[i][j] != INFINT && i != j) {
            return j; // 返回邻接点的索引
        }
        
        //如果是有向图，第一个邻接点可能源自于入边 
        if (G.isUndirected==0 &&G.arcs[j][i] != INFINT && i != j) {
            return j; // 返回邻接点的索引
        }        
    }
    return -1; // 没有邻接点
}

十二、求顶点 x 的下一个邻接点 

假设图中顶点y是顶点x的一个邻接点，返回除y外顶点x的下一个邻接点的顶点号，若y是x的最后一个邻接点，则返回-1 

// 求顶点 x 的下一个邻接点
int NextNeighbor(MGraph G, VerTexType x, VerTexType y) {
    int i = -1, j = -1;

    // 查找顶点 x 和 y 的索引
    for (int k = 0; k < G.vexnum; k++) {
        if (G.vexs[k] == x) i = k;
        if (G.vexs[k] == y) j = k;
    }

    if (i == -1 || j == -1) {
        printf("顶点 %c 或 %c 不存在\n", x, y);
        return -1;
    }

    // 查找下一个邻接点
    for (int k = j + 1; k < G.vexnum; k++) {
        if (G.arcs[i][k] != INFINT && i != k) {
            return k;
        }
		 
        //如果是有向图，则下一个邻接点可能源自于入边 
        if (G.isUndirected==0 && G.arcs[k][i] != INFINT && i != k) {
            return k;
        }
    }

    return -1; // 没有下一个邻接点
}

十三、获取边的权值

// 获取边的权值
ArcType Get_edge_value(MGraph G, VerTexType x, VerTexType y) {
    int i = -1, j = -1;

    // 查找顶点 x 和 y 的索引
    for (int k = 0; k < G.vexnum; k++) {
        if (G.vexs[k] == x) i = k;
        if (G.vexs[k] == y) j = k;
    }

    if (i != -1 && j != -1) {
        return G.arcs[i][j];
    }

    printf("边 (%c, %c) 不存在\n", x, y);
    return -1;
}

十四、设置边的权值

// 设置边的权值
void Set_edge_value(MGraph &G, VerTexType x, VerTexType y, ArcType v) {
    int i = -1, j = -1;

    // 查找顶点 x 和 y 的索引
    for (int k = 0; k < G.vexnum; k++) {
        if (G.vexs[k] == x) i = k;
        if (G.vexs[k] == y) j = k;
    }

    if (i != -1 && j != -1) {
        G.arcs[i][j] = v;
        if(G.isUndirected)  G.arcs[j][i] = v;  // 无向图需设置两个方向
    } else {
        printf("边 (%c, %c) 不存在\n", x, y);
    }
}

您可能感兴趣的与本文相关的镜像

ACE-Step

ACE-Step

音乐合成
ACE-Step

ACE-Step是由中国团队阶跃星辰（StepFun）与ACE Studio联手打造的开源音乐生成模型。 它拥有3.5B参数量，支持快速高质量生成、强可控性和易于拓展的特点。 最厉害的是，它可以生成多种语言的歌曲，包括但不限于中文、英文、日文等19种语言

基于邻接矩阵的Dijkstra算法——C++实现
程序必须为人类阅读而编写，并且仅仅碰巧可以让机器执行
06-01 1217
本文实现的Dijkstra(迪杰斯特拉)算法包含如下功能： 1. 可指定起始点和初始点 2. 能够计算起始点和初始点之间的最短路径长度 3. 能够输出起始点和初始点之间的最短路径(中间节点)
C语言邻接矩阵和邻接表的相互转换算法讲解,图——邻接矩阵和邻接表基本存储及转换算法...
weixin_28683689的博客
05-24 1709
代码基于：【数据结构】【严蔚敏】【清华大学】【邻接矩阵和邻接表相互转换算法】 问题描述：该算法的设计，要求运行结果如下所示： 图 G 的邻接矩阵: 0 1 1 0 0 0 0 0 1 0 0 1 1 0 0 0 1 0 0 0 0 1 1 0 0 1 0 0 0 0 0 1 0 1 0 0 0 0 0 1 0 0 1 0 0 0 1 0 0 0 1 0 0 1 0 0 0 0 0 1 1 0 0 ...
数据结构与算法-图结构 | 尚硅谷韩顺平
weixin_54232666的博客
10-05 491
想弄懂数据结构与算法-图结构，这一篇就够了！包括图的介绍，图的深度遍历和广度遍历的思路和代码实现。
Dijkstra算法——邻接矩阵实现+路径记录
胡海龙
01-08 1105
本文章介绍了如何实现图的邻接矩阵，并通过邻接矩阵实现 Dijkstra 最短路径算法，文章提供了完整的邻接矩阵实现代码和 Dijkstra 实现代码。 并提供了完整的测试用例，打印最短距离和记录路径信息。
图——邻接矩阵 DFS、BFS（C语言实现）
且视他人之疑目如盏盏鬼火
12-02 341
/访问数组(用来确定元素是不是已经被访问)EdgeType Edge[MaxVexNum][MaxVexNum];//用静态数组存放队列元素。#define MaxVexNum 100//顶点数目的最大值。//队头指针和队尾指针。//DFSTraverse(防止非连通图)//BFSTraverse(防止非连通图)//输入边(此处用无向图举例)//打印图的邻接矩阵。
图——邻接矩阵和邻接表基本存储及转换算法
○( ＾皿＾)っHiahiahia…的博客
12-23 9394
代码基于：【数据结构】【严蔚敏】【清华大学】 【邻接矩阵和邻接表相互转换算法】 问题描述：该算法的设计，要求运行结果如下所示： 图 G 的邻接矩阵: 0 1 1 0 0 0 0 0 1 0 0 1 1 0 0 0 1 0 0 0 0 1 1 0 0 1 0 0 0 0 0 1 0 1 0 0 0 0 0 1 0 0 1 0 0 0 1 0 0 0 1 0 0 1 0 0 0 0 0 1 1 0 0...
图——邻接矩阵
zhuziyuzzy的博客
05-02 4440
*图的储存*///点的数量//定义点集合数组v[i]=j;第i个结点的编号是jstruct edges{//单条边结构体int from;//该条边的左顶点int to;//该条边的右顶点double w;//边的长度//边集合int cnt=1;//当前在读入第cnt条边//记录第cnt条边的左顶点是u//记录第cnt条边的右顶点是ve[cnt].w=w;////记录第cnt条边的权值cnt++;//换下一条边去读/*邻接矩阵*///
数据结构——邻接矩阵
分享大数据、人工智能领域原创文章
10-21 535
无权图：若顶点( v_i )与( v_j )间有边（无向图）或弧（有向图，( v_i )指向( v_j )），则( A[i][j] = 1 )；否则( A[i][j] = 0 )（或用特殊值标记“无连接”）。带权图（网）：若顶点( v_i )与( v_j )间有边/弧，且权值为( w_{ij} )，则( A[i][j] = w_{ij} )；否则( A[i][j] )用“无穷大（( \infty )）”或特殊标记表示“无连接且无权值”。
Python——数据结构——图——邻接矩阵
qq_41188247的博客
01-07 4578
Python——数据结构——图——邻接矩阵
Transcad——邻接矩阵
yyua0006的博客
04-13 643
邻接矩阵是用来表达小区之间的相邻关系的。
基于图卷积神经网络的创新数据分类预测系统——GCN分类算法的Matlab实现 · 邻接矩阵
08-01
GCN分类技术通过将不同特征视为节点并以邻接矩阵表示它们之间的相关系数，从而提供了一种全新的数据分类预测手段。该系统的运行环境要求MATLAB版本为2022b及以上，已提供的测试数据集可以直接用于源程序运行，且代码...
数据结构实验——实现图的邻接矩阵和邻接表存储以及实现图的遍历算法
u014114223的博客
11-18 3275
CreateMat(MatGraph &g,int A[MAXV][MAXV],int n,int e):由边数组A、顶点数n和边数e创建图的邻接矩阵g。·DFSl(AdjGraph*G,intv):以非递归的方法从顶点v深度优先遍历图G。(2)输出如图8.1所示的有向图G中从顶点0开始的深度优先遍历序列(非递归算法)。·DFS(AdjGraph*G,intv):以递归的方法从顶点v深度优先遍历图G。(1)输出如图8.1所示的有向图G中从顶点0开始的深度优先遍历序列(递归算法)。
力扣hot100：搜索二维矩阵
一本大学生java学习技术分享与交流
12-14 284
二分查找返回的是目标值最先出现的位置或者是在有序数组中的插入位置，如果是在有序数组中的插入位置则可能为在数组最后一个位置加一个数，这是如果进行matrix[i][weizi]==target的判断的话会导致数组越界，必须先处理越界问题，最终判断条件应为weizi<matrix[i].length&&matrix[i][weizi]==target。本题的本质是一个查找算法，为了提高性能可以使用二分查找，这个二维矩阵可以看出许多个数组，只需要对每个数组都进行一次二分查找就可以实现查找整个二维矩阵。
Louvain 算法
FionaDong的博客
12-12 229
Louvain 是一种经典的图社区发现算法（Community Detection），由 Blondel 等人在 2008 年提出。核心目标：通过最大化 Modularity（模块度）来自动划分图中的社区（cluster）。它最大的特点是：✔ 速度非常快✔ 能处理百万级节点的大图✔ 结果相对稳定。
智驾空间智能、物理智能、世界模型相关的最新论文和开源算法链接
Bonaventure的博客
12-16 883
这些资源涵盖了2025年自动驾驶领域的前沿研究，从空间推理到物理建模和世界模拟，提供了丰富的开源工具和理论框架。建议用户通过链接深入探索论文和代码，以应用于实际项目或进一步研究。如果您需要更详细的解读或特定应用建议，请随时补充信息！
从零开始写算法——链表篇4:删除链表的倒数第 N 个结点 + 两两交换链表中的节点
m0_59624833的博客
12-15 776
hot100链表的两道题详解。
JVM 之 垃圾回收算法及其内部实现原理【垃圾回收的核心问题有哪些？分别怎么解决的？可达性分析解决了什么问题？回收算法有哪些？内部怎么实现的？】
人生快意事，读的好书，觅得良友
12-16 1097
JVM垃圾回收面临的核心问题有哪些？分别怎么解决的？ 可达性分析解决了什么问题？回收算法有哪些？内部怎么实现的？ 根节点枚举、安全点、安全区域、记忆集与卡表、写屏障、并发性可达性分析各自解决了什么问题？怎么协同工作的？ G1中他们是怎么协作的？
Leetcode 79 最佳观光组合
最新发布
im_AMBER的博客
12-17 358
每个元素只遍历一次只用了两个变量O(n)O(1)公式拆分是核心：将原得分公式拆分为，把双变量问题转化为单变量的遍历问题。贪心维护最优值：遍历j时，用best维护之前所有i < j中的最大值，这样每一步只需要 O (1) 计算，整体时间复杂度是 O (n)。遍历顺序：因为要求i < j，所以从j=1开始遍历，先计算当前j的得分，再更新best（避免 j 自己和自己配对）。
二分答案算法详解：从理论到实践解决最优化问题
2401_86619696的博客
12-12 915
文章记录了何为二分法，二分法怎么用，以及二分查找。主要详细讲了二分答案，讲了二分答案的模板，以及一部分题
MATLAB实现最短路径算法——基于输入邻接矩阵
算法的基本思想是动态规划，通过迭代计算逐渐更新邻接矩阵中的元素值。在每一步迭代中，算法会尝试通过中间顶点k更新顶点i到顶点j的最短路径。如果通过顶点k的路径比已知的直接路径更短，则更新矩阵中的对应值。经过...
评论
成就一亿技术人!
拼手气红包6.0元
还能输入1000个字符
 
红包 添加红包
表情包 插入表情
表情包 代码片
 条评论被折叠 查看
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值