Python数学建模

python数学建模

本人学习用python数学建模，争取当一个编程手。（持续更新中。。。。。）
内容可能会借鉴别人的，只做学习用途，如有侵权，请联系我删除
如有错误欢迎指正

numpy库的基本使用

NumPy 通常与 SciPy（Scientific Python）和 Matplotlib（绘图库）一起使用优点是速度快，比python自带的列表要快很多

NumPy - Ndarray 对象

Scipy库的基本使用

linprog函数

用来求解线性规划问题

def linprog(c,A_ub=None, b_ub=None, A_eq=None, b_eq=None,bounds=None, method='interior-point', callback=None,options=None, x0=None)

参数	意义
c	求解目标函数的系数向量(一维数组)
A_ub	不等式约束矩阵， Aub 的每一行指定x 上的线性不等式约束的系（二维数组）
b_ub	由A_ub对应不等式顺序的阈值向量（一维数组）
A_eq	等式约束组成的决策变量系数矩阵（二维数组）
b_eq	由A_ub对应等式顺序的阈值向量（一维数组）
bounds	表示决策变量x连续的定义域的n×2维矩阵，None表示无穷（x的最小值和最大值）
method	调用的求解方法 {‘interior-point’, ‘revised simplex’, ‘simplex’}
callback	选择的回调函数
options	求解器选择的字典
x0	初始假设的决策变量向量，若可行linprog会对方法优化

输出格式

参数	意义
x	在满足约束的情况下将目标函数最小化的决策变量的值
fun	目标函数的最佳值
slack	不等式约束的松弛值（名义上为正值）b_u b − A_ub x
con	等式约束的残差（名义上为零）
success	当算法成功找到最佳解决方案时为 True
status	表示算法退出状态的整数 0 : 优化成功终止1 : 达到了迭代限制2 : 问题似乎不可行3 : 问题似乎是不收敛4 : 遇到数值困难
nit	在所有阶段中执行的迭代总数
message	算法退出状态的字符串描述符

odeint函数

scipy.integrate.odeint(func, y0, t, args=(), Dfun=None, col_deriv=0, full_output=0, ml=None, 
mu=None, rtol=None, atol=None, tcrit=None, h0=0.0, hmax=0.0, hmin=0.0, ixpr=0, mxstep=0, 
mxhnil=0, mxordn=12, mxords=5, printmessg=0, tfirst=False)

参数	意义
func	自行定义的求解的微分方程的函数
y0	微分方程的初值（可以是一个元组，顺序要对应）
t	微分方程的自变量，应该是一个连续的序列值

Pulp库的基本使用

PuLP是一个开源的第三方工具包，可以求解线性规划、整数规划、混合整数规划问题。

三个基本函数

LpProblem(name=‘NoName’, sense=LpMinimize)#定义问题
solve(solver=None, **kwargs)#解决问题
LpVariable(name, lowBound=None, upBound=None, cat=‘Continuous’, e=None)#定义变量

Sympy库的基本使用

sympy的全称是Symbolic Python，是一款用于符号运算的python库。SymPy的真正强大之处是做各种类型的符号计算。SymPy可以符号形式地简化表达式、计算导数、积分和极限、解方程、处理矩阵等等。

matplotlib.pyplot库的基本使用

（一）规划问题之线性规划

线性规划求解需要清晰两部分，目标函数(max, min) 和 约束条件 ，求解前应转化为标准形式：

使用的是scipy.optimize.linprog函数来解决

使用例子

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-JPFxaFM3-1684412080182)(C:\Users\15858\Pictures\Screenshots\屏幕截图 2023-05-07 164716.png)]

scipy库求解

from scipy import optimize
import numpy as np
c = np.array([2,3,-5])#将目标函数的系数存入numpy中 一维数组
A = np.array([[-2,5,-1],[1,3,1]])#将不等式约束条件系数存入数组中 二维数组
B = np.array([-10,12])#将不等式约束条件的右边存入数组中
Aeq = np.array([[1,1,1]])#将等式的系数放入数组中
Beq = np.array([7])#将等式的右边放入数组Beq中
res = optimize.linprog(-c,A,B,Aeq,Beq)#进行求解
print(res)

求解结果

           con: array([0.])
 crossover_nit: 0
         eqlin:  marginals: array([-2.28571429])
  residual: array([0.])
           fun: -14.571428571428571 #最优值
       ineqlin:  marginals: array([-0.14285714, -0.        ])
  residual: array([0.        , 3.85714286])
         lower:  marginals: array([0.        , 0.        , 7.14285714])
  residual: array([6.42857143, 0.57142857, 0.        ])
       message: 'Optimization terminated successfully. (HiGHS Status 7: Optimal)'
           nit: 3
         slack: array([0.        , 3.85714286])
        status: 0
       success: True
         upper:  marginals: array([0., 0., 0.])
  residual: array([inf, inf, inf])
             x: array([6.42857143, 0.57142857, 0.        ])#对应决策变量的值 从左到右依次表示x1，x2,x3

对很大/小的数不使用科学计数法 np.set_printoptions(suppress=True)

使用plup库求解

例题

import pulp as pp

# 目标函数的系数
z = [2, 3, 1]
a = [[1, 4, 2], [3, 2, 0]]
b = [8,6]
aeq = [[1,2,4]]
beq = [101]

# 确定最大最小化问题，当前确定的是最大化问题
m = pp.LpProblem(sense=pp.LpMaximize)

# 定义三个变量放到列表中
x = [pp.LpVariable(f'x{i}', lowBound=0) for i in [1, 2, 3]]

# 定义目标函数，并将目标函数加入求解的问题中
m += pp.lpDot(z, x) # lpDot 用于计算点积

# 设置比较条件
for i in range(len(a)):
    m += (pp.lpDot(a[i], x) >= b[i])

# 设置相等条件
for i in range(len(aeq)):
    m += (pp.lpDot(aeq[i], x) == beq[i])

# 求解
m.solve()
# 输出结果
print(f'优化结果：{pp.value(m.objective)}')
print(f'参数取值：{[pp.value(var) for var in x]}')

（二）规划问题之整数规划

（三）规划问题之非线性规划

（四）微分方程求解

前言

常微分方程建模是数学建模的重要方法，因为许多实际问题的数学描述将导致求解常微分方程的定解问题。把形形色色的实际问题化成常微分方程的定解问题，大体上可以按以下步骤：

（1）根据实际要求确定要研究的量(自变量、未知函数、必要的参数等)并确定坐标系。

（2）找出这些量所满足的基本规律(物理的、几何的、化学的或生物学的等等)。

（3）运用这些规律列出方程和定解条件。

求解方式：
（1）解析解法（精确解）

（2）数值解法（近似值）就是将x离散化，求得每一个x对应的近似y

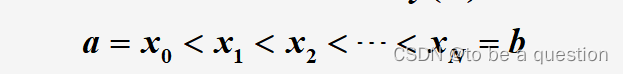
求解思路

用差商近似导数

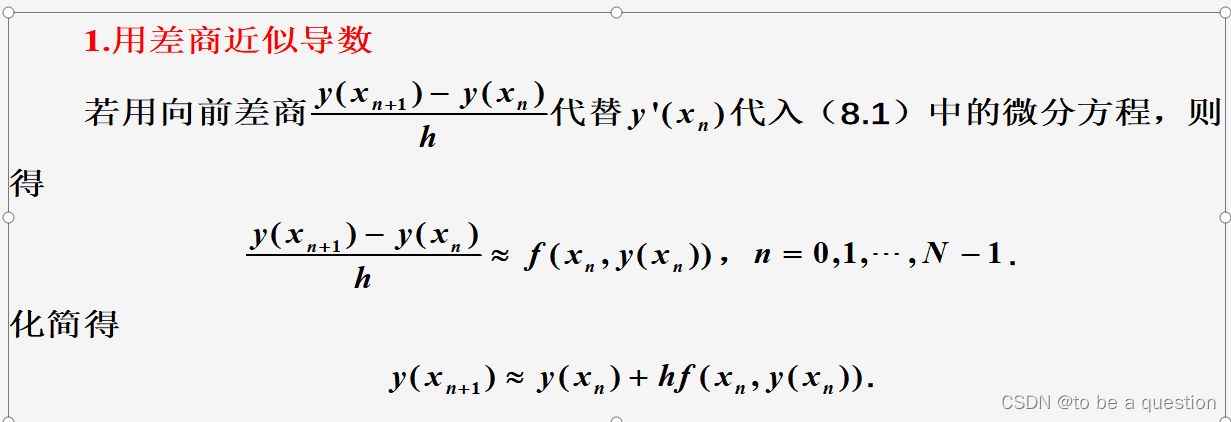
用数值积分方法

泰勒多项式近似

用python求解微分方程

解析解法

具备解析解的ODE（常微分方程），我们可以利用SymPy库进行求解

例子

代码

#程序文件Pex8_1.py
from sympy.abc import x
from sympy import diff, dsolve, simplify, Function
y=Function('y')
eq=diff(y(x),x,2)+2*diff(y(x),x)+2*y(x)  #定义方程
con={y(0): 0, diff(y(x),x).subs(x,0): 1}  #定义初值条件
y=dsolve(eq, ics=con)
print(simplify(y))

求得

具备解析解的ODE（常微分方程），我们可以利用SymPy库进行求解

以求解阻尼谐振子的二阶ODE为例，其表达式为：

Demo代码

import sympy
 
 
def apply_ics(sol'''微分方程的解''',ics, x, known_params):#应用初始条件
    free_params = sol.free_symbols - set(known_params)
    eqs = [(sol.lhs.diff(x, n) - sol.rhs.diff(x, n)).subs(x, 0).subs(ics) for n in range(len(ics))]
    sol_params = sympy.solve(eqs, free_params)
    return sol.subs(sol_params)
 
 
# 初始化打印环境
sympy.init_printing()
# 标记参数，且均为正
t, omega0, gamma = sympy.symbols("t, omega_0, gamma", positive=True)
# 标记x是微分函数，非变量
x = sympy.Function("x")
# 用diff()和dsolve得到通解 
# ode 微分方程等号左边的部分，等号右边为0
ode = x(t).diff(t, 2) + 2 * gamma * omega0 * x(t).diff(t) + omega0 ** 2 * x(t)
ode_sol = sympy.dsolve(ode)
# 初始条件：字典匹配
ics = {x(0): 1, x(t).diff(t).subs(t, 0): 0}
x_t_sol = apply_ics(ode_sol, ics, t, [omega0, gamma])
sympy.pprint(x_t_sol)#表达式的简化与打印

#——————————————另一种写法————————————————#

import sympy

# 初始化打印环境
sympy.init_printing()
# 标记参数，且均为正
t, omega0, gamma = sympy.symbols("t, omega_0, gamma", positive=True)
# 标记x是微分函数，非变量
x = sympy.Function("x")
# 用diff()和dsolve得到通解 
# ode 微分方程等号左边的部分，等号右边为0
ode = x(t).diff(t, 2) + 2 * gamma * omega0 * x(t).diff(t) + omega0 ** 2 * x(t)

# 初始条件：字典匹配
ics = {x(0): 1, x(t).diff(t).subs(t, 0): 0}
ode_sol = sympy.dsolve(ode ,ics=ics)#添加初始化条件和微分方程
sympy.pprint(ode_sol)#表达式的简化与打印

数值解法

当ODE无法求得解析解时，可以用scipy中的integrate.odeint求 数值解来探索其解的部分性质,并辅以可视化，能直观地展现 ODE解的函数表达。

Python对常微分方程的数值求解是基于一阶方程进行的，高阶微分方程必须化成一阶方程组，通常采用龙格—库塔方法。scipy.integrate模块的odeint函数求常微分方程的数值解，其基本调用格式为：

sol=odeint(func, y0, t)

例子

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-WNDJFF0t-1684412080183)(C:\Users\15858\AppData\Roaming\Typora\typora-user-images\image-20230509161633671.png)]

#程序文件Pex8_4.py
from scipy.integrate import odeint
from numpy import arange
dy=lambda y, x: -2*y+x**2+2*x
x=arange(1, 10.5, 0.5)
sol=odeint(dy, 2, x)
print("x={}\n对应的数值解y={}".format(x, sol.T))

#程序文件Pex8_5.py
from scipy.integrate import odeint
from sympy.abc import t
import numpy as np
import matplotlib.pyplot as plt
def Pfun(y,x):
    y1, y2=y;
    return np.array([y2, -2*y1-2*y2])
x=np.arange(0, 10, 0.1)  #创建时间点
sol1=odeint(Pfun, [0.0, 1.0], x)  #求数值解
plt.rc('font',size=16); plt.rc('font',family='SimHei')
plt.plot(x, sol1[:,0],'r*',label="数值解")
plt.plot(x, np.exp(-x)*np.sin(x), 'g', label="符号解曲线")
plt.legend(); plt.savefig("figure8_5.png"); plt.show()