【通俗易懂从小白开始学数学】：两个极限公式推导以及了解夹逼定理跟洛必达法则

 前言：

因为这种章涉及到很多公式，不好打出，故都采用图片分享，希望对你们有所帮助，喜欢的帮忙一键三连。

 

 

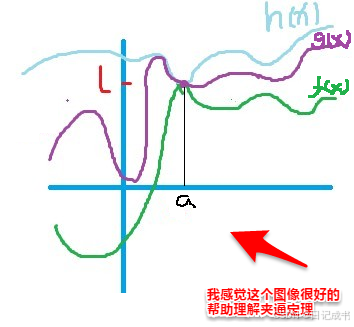
夹逼定理：

1.夹逼定理是判定数列或函数的极限存在、求数列或函数的极限的一个重要方法（它的核心思想是通过找到两个较为简单的函数，将待求极限夹在它们之间，从而推导出原始极限的结果）

2.夹逼准则的条件： 为了使用夹逼准则，以下条件必须满足：

在某一点a的去心邻域内，存在两个函数f(x)和h(x)，满足对于所有的x，都有 f(x)≤g(x)≤h(x)。

当x趋近于a时，函数f(x)和h(x)都收敛到同一个极限L，即lim(x→a)f(x)=lim(x→a)h(x)= L。

洛必达法则:

1.洛必达法则是在一定条件下通过分子分母分别求导再求极限来确定原分式极限的方法，其实这是由瑞士数学家伯努利发现的，只不过当时洛必达买走了伯努力的知识产权，后来以洛必达命名。

需要注意的事项：

极限形式为0/0或∞/∞，即分子和分母分别趋向于零或无穷大（面对极限题型的时候首先判断分子分母的极限是不是都等于零或者无穷）

可导性要求：洛必达法则要求函数在考虑的区间内是可导的，且分母的导数不能为零。

非洛必达形式的处理：对于非洛必达形式的问题，需要通过代数技巧或其他极限计算方法来处理。

 下一章预告：泰勒级数