拟合回归中的误差计算

趣知boy

已于 2023-04-24 15:54:36 修改

阅读量4.5k

点赞数

分类专栏：机器学习文章标签：回归机器学习算法

于 2023-04-24 15:41:48 首次发布

本文链接：https://blog.csdn.net/m0_67794575/article/details/129302953

版权

机器学习专栏收录该内容

6 篇文章

订阅专栏

常用度量

1.MAE（平均绝对误差）

2.RMSE（均方根误差）

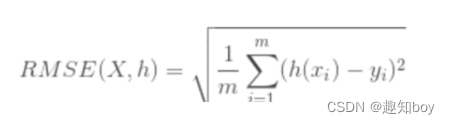
3.MSE（均方误差）

%matlab中mse计算
mse=mse(T_sim-t_test); %T_sim为预测值  t_test为实际值

4.R^2非线性模型

%matlab计算R^2
N = size(t_test,1);   % t_test为行向量 N为行向量或者列向量得维数
R2=(N*sum(T_sim.*t_test)-sum(T_sim)*sum(t_test))^2/((N*sum((T_sim).^2)-(sum(T_sim))^2)*(N*sum((t_test).^2)-(sum(t_test))^2))  %T_sim预测值   t_test为实际值

5.R2线性模型

6.交叉验证：

交叉验证是在机器学习中创建模型和验证模型参数时常用的方法。

为什么需要cv？

在训练集（train set）上训练得到的模型表现良好，但在测试集（test set）的预测结果不尽如人意，这就说明模型可能出现了过拟合（overfitting），bias低而variance高，在未知数据上的泛化能力差。

一个改进方案是，在训练集的基础上进一步划分出新的训练集和验证集（validate set），在新训练集训练模型，在验证集测试模型，不断调整初始模型（超参数等），使得训练得到的模型在验证集上的表现最好，最后放到测试集上得到这个最优模型的评估结果。

这个方案的问题在于模型的表现依赖于验证集的划分，可能使某些特殊样本被划入验证集，导致模型的表现出现异常（偏好或偏差）。而且训练集划了一部分给验证集后，训练模型能得到的数据就变少了，也会影响训练效果。因为通常来说，训练数据越多，越能反映出数据的真实分布，模型训练的效果就越好，越可能得到无偏估计。

交叉验证思想应运而生，交叉验证可以充分使用所有的训练数据用于评估模型。
————————————————
版权声明：本文为CSDN博主「CtrlZ1」的原创文章，遵循CC 4.0 BY-SA版权协议，转载请附上原文出处链接及本声明。
原文链接：https://blog.csdn.net/qq_41076797/article/details/102730862

不同的超参数可能会导致我们训练出来不同的模型,也直接会影响到我们模型的表现。那么该如何调整或者说设置这些参数呢?我们就会用到交叉验证。