【仅供参考】Csapp第五章课后习题答案（欢迎批评指正）

最新推荐文章于 2023-03-18 20:48:52 发布

只会c语言

最新推荐文章于 2023-03-18 20:48:52 发布

阅读量3.2k

点赞数 1

文章标签： c语言

本文链接：https://blog.csdn.net/m0_68072963/article/details/124531322

版权

本文探讨了代码性能优化的策略，通过分析关键路径上的操作，如浮点数加法和乘法的CPE（计算性能评估），以及如何通过并行计算和循环展开来提升效率。例如，`inner4`函数的优化减少了迭代次数但保持了乘法操作，而`effective_memset`函数通过地址对齐和批量设置提高了内存操作效率。同时，`polynew`函数利用了多项式计算的特性来减少重复计算。这些方法在实际编程中对于提高代码运行速度具有重要意义。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

5.13

【答案】

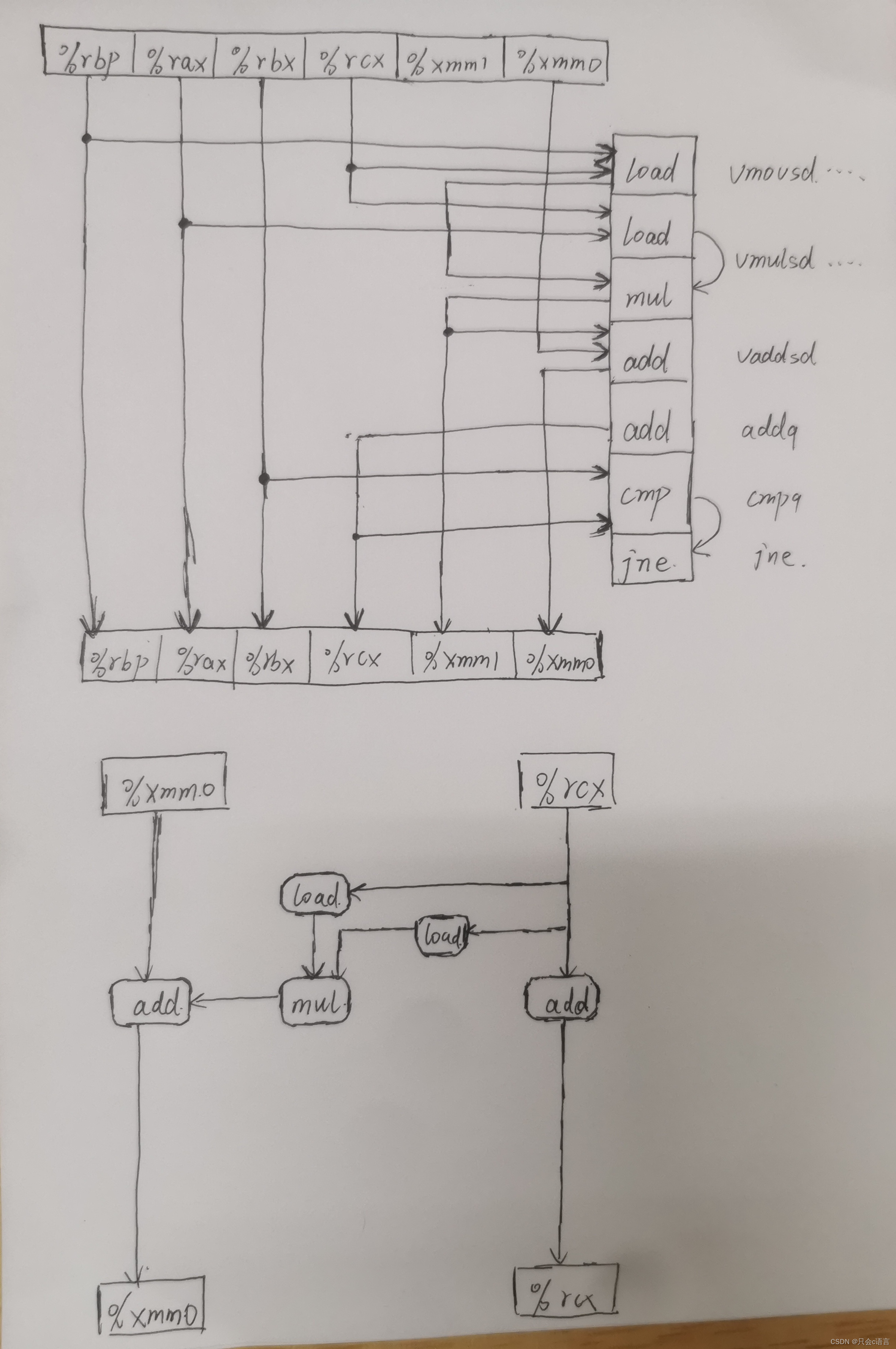
B.3.0

C.1.0

D.浮点乘法不在关键路径上。

【解释】

A.如图

B.关键路径上只有浮点数加法CPE为3.0

C.整数加法的CPE为1.0

D.结合图理解。

5.14

【答案】

void inner4(vec_ptr u, vec_ptr v, data_t *dest) {
  long i;
  long length = vec_length(u);
  data_t *udata = get_vec_start(u);
  data_t *vdata = get_vec_start(v);
  data_t sum = (data_t) 0;
  for (i = 0; i < length-6; i+=6) {
    sum = sum + udata[i] * vdata[i]
              + udata[i+1] * vdata[i+1]
              + udata[i+2] * vdata[i+2]
              + udata[i+3] * vdata[i+3]
              + udata[i+4] * vdata[i+4]
              + udata[i+5] * vdata[i+5];
  }
  for(; i < length; i++) {
    sum = sum + udata[i] * vdata[i];
  }
  *dest = sum;
}

A.虽然迭代次数减少为6/n，但是每次迭代中有6个乘法操作，所以关键路径上还是一共有n个乘法操作。

B.与上面相同

5.15

【答案】

void inner4(vec_ptr u, vec_ptr v, data_t *dest) {
  long i;
  long length = vec_length(u);
  data_t *udata = get_vec_start(u);
  data_t *vdata = get_vec_start(v);
  data_t sum = (data_t) 0;
  data_t sum1 = (data_t) 0;
  data_t sum2 = (data_t) 0;
  data_t sum3 = (data_t) 0;
  data_t sum4 = (data_t) 0;
  data_t sum5 = (data_t) 0;
  for (i = 0; i < length-6; i+=6) {
    sum = sum + udata[i] * vdata[i];
    sum1 = sum1 + udata[i+1] * vdata[i+1];
    sum2 = sum2 + udata[i+2] * vdata[i+2];
    sum3 = sum3 + udata[i+3] * vdata[i+3];
    sum4 = sum4 + udata[i+4] * vdata[i+4];
    sum5 = sum5 + udata[i+5] * vdata[i+5];
  }
  for(; i < length; i++) {
    sum = sum + udata[i] * vdata[i];
  }
  *dest = sum + sum1 + sum2 + sum3 + sum4 + sum5;
}

因为只有两个加载器

5.16

【答案】

只需要用括号将后面两两括起来，括哪两个都可以，只要是两两括起来就可以。

void inner4(vec_ptr u, vec_ptr v, data_t *dest) {
  long i;
  long length = vec_length(u);
  data_t *udata = get_vec_start(u);
  data_t *vdata = get_vec_start(v);
  data_t sum = (data_t) 0;
  for (i = 0; i < length-6; i+=6) {
    sum = sum + (udata[i] * vdata[i]
              + (udata[i+1] * vdata[i+1]
              + (udata[i+2] * vdata[i+2]
              + (udata[i+3] * vdata[i+3]
              + (udata[i+4] * vdata[i+4]
              + (udata[i+5] * vdata[i+5])))));
  }
  for(; i < length; i++) {
    sum = sum + udata[i] * vdata[i];
  }
  *dest = sum;
}

5.17

【答案】

void effective_memset(void *s, int c, size_t n){
    unsigned long newc = (unsigned long)(1+(2<<8)+(2<<16)+(2<<24)+(2<<32)+
                        (2<<40)+(2<<48)+(2<<56))*(unsigned char);  
    size_t K = sizeof(unsigned long);                         #newc是用unsigned long
    size_t cnt = 0;                                            类型的数据保存8个c。
    unsigned char *schar = s;                                 #此处的循环目的是地址对齐
    while((size_t)schar % K == 0){
        *schar++ = (unsigned char)c;
        cnt++;
    }
    
    size_t rest = n - cnt;
    size_t part1 = rest / K;
    size_t part2 = rest % K;
    unsigned long *spart1 = (unsigned long *)schar;           #此处目的地址为K的倍数
    size_t i;                                                  使用字级的写
    for(i = 0; i < part1; i++){
        *spart1++ = newc;
    };

    schar = (unsigned char *)spart1;                          #最后的收尾再回到字节级的写
    for(i = 0; i < part2; i++){
        *schar++ = (unsigned char)c;
    };
    return s;
}

5.18

【答案】

double polynew(double a[], double x, long degree) {
  long i = 1;
  double result = a[0];
  double result1 = 0;
  double result2 = 0;
  double xpwr = x;
  double xpwr1 = x * x * x;
  double xpwr2 = x * x * x * x * x;
  double xpwr_loop = x * x * x * x * x * x;
  for (; i <= degree - 6; i+=6) {
    result = result + (a[i]*xpwr + a[i+1]*xpwr*x);
    result1 = result1 + (a[i+2]*xpwr1 + a[i+3]*xpwr1*x);
    result2 = result2 + (a[i+4]*xpwr2 + a[i+5]*xpwr2*x);
    xpwr *= xpwr_loop;
    xpwr1 *= xpwr_loop;
    xpwr2 *= xpwr_loop;
  }
  
  for (; i <= degree; i++) {
    result = result + a[i]*xpwr;
    xpwr *= x;
  }
  return result + result1 + result2;
}

5.19

【答案】

void psumnew(float a[], float p[], long n) {
  long i;
  float val, last_val;
  float tmp1, tmp2, tmp3, tmp4;
  last_val = p[0] = a[0];
  for (i = 1; i < n - 4; i++) {
    temp1 = last_val + a[i];
    temp2 = temp1 + a[i+1];
    temp3 = temp2 + a[i+2];
    temp4 = temp3 + a[i+3];
    p[i] = temp1;
    p[i+1] = temp2;
    p[i+2] = temp3;
    p[i+3] = temp4;
    last_val = temp4;
  }
  for (; i < n; i++) {
    last_val += a[i];
    p[i] = last_val;
  }
}