提示:本篇只介绍了常用的三种校验码
目录
前言
计算机系统运行时,各个部件之间要进行数据交换,为了确保数据在传送过程中正确无误,一是提高硬件电路中的可靠性;二是提高代码的校验能力,包括查错和纠错。通常使用效验码的方法来检测传送的数据是否出错,即对数据可能出现的编码分为两类:合法编码和错误编码。合法编码用于传送数据,错误编码是不允许在数据中出现的编码。合理的设计错误编码以及编码规则,使得数据在传送中出现某种错误是就会变成错误编码,这样就可以检测出接收到的数据是否有误。
码距是效验码中的一个重要概念。所谓码距,是指一个编码系统中任意两个合法编码之间至少有多少个二进制不同。例如,1000,1001码距为1 1000, 1011码距为2,码距的计算是对两个编码进行异或运算,并计算出语或运算结果中1的个数。4位8421码的码距为1,在传输过程中,该代码的一位或者多位发生错误,都将变成另外一个合法编,因此这种代码无差错检验能力。8421码是一种BCD码,其中每一位的“1”都代表一个固定的十进制数值。 从左到右看,每一位“1”分别代表数字“8”、“4”、“2”、“1”,因此得名8421码。 这种编码方式中,每位的权都是固定不变的,因此8421码是恒权码。
下面简单介绍常用的三种效验码:奇偶效验码(Parity Codes)、海明码(Hamming Code)和循环冗余校验(Cyclic Redundancy Check, CRC)码。
一、奇偶效验码
奇偶效验是一种简单有效的校验方法。这种方法通过在编码中增加一个校验位来使编码中1的个数为奇数(奇校验)或者偶数(偶校验)从而使码距变为2,对于奇偶校验,它可以检测代码中奇数位出错的代码,但不能发现哦偶数位出错的情况,即当合法编码中奇数位发生了错误,也就是编码中的1变成了0或0变成1,则该编码中1的个数的就行就发生了变化,从而可以发现错误。8421码的奇偶校验码如下所示。

从中可以看出,带奇偶校验位的8421码由4位信息为和一位校验位组成,码距为2,能检查出代码信息中的奇数位出错的情况,而错在哪些位置检查不出来的。也就是说,它只能发现错误,而不能校正错误。
常用的奇偶效验码有3种:水平奇偶校验码,垂直奇偶校验码和水平垂直校验码。
1.水平奇偶校验码
水平奇偶校验码。对每一个数据的编码添加校验位,使信息位与校验位处于同一行。
2.垂直奇偶校验码
垂直奇偶校验码。这种校验码把数据分成若干组,一组数据占一行,排列整齐,再加一行校验码,针对每一列采用奇校验或偶校验。
对于32位数据10100101 00110110 11001100 10101011,其中垂直奇校验和垂直偶校验如下所示。

3.水平垂直校验码
水平垂直校验码。在垂直校验码的基础上,对每个数据再增加一位水平校验码,便构成水平垂直校验码。
对于32位数据10100101 00110110 11001100 10101011,其水平垂直奇校验和偶校验如下所示:

二、海明码
1.校验位数
海明码也是利用奇偶性来检查和纠错的校验方法。海明码的构成方法是:在数据为之间插入k个校验位,通过该扩大码距来实现检错和纠错。
关于信息码对应的校验码位数如下所示,一般死记硬背。
例如,对于8位的数据位,进行海明校验需要4个校验位。另数据位D7、D6、D5、D4、D3、D2、D1、D0,校验位为P4、P3、P2、P1,形成的海明码为H12、H11、H10、H9、H8、H7、H6、H5、H4、H3、H2、H1,则编码过程如下。
2.校验位计算
(1)首先确定数据位与校验位在海明码中的位置,如下所示
校验位设置在2^i位置,因此P1对应H1,P2对应H2,P3对应H4,P4对应H8。
每个校验位只校验数据中位置号的二进制编码和自身位置号的二进制编码相匹配的数据位。例如,D3(H7)的位置号为7(=4+2+1),因此该数据位由P1、P2和P3校验。

(2)通过校验关系,确定各个校验位的值。

若采用奇校验,则将各校验位的偶校验值取反即可。
3.检测错误
(3)检测错误,对使用海明编码的数据进行差错检测很简单,只需做一下计算:

若采用偶校验,则G4 G3 G2 G1全为0时表示接受到的数据无错误(奇校验则应全为1)。当G4 G3 G2 G1 不全为0说明发生了错误,而且G4 G3 G2 G1 的十进制值指出发生错误的位置。例如G4G3G2G1 = 1010,说明H10(D5)出错了,将其取反即可纠正错误。
4. 例题
例:设数据为01101001,试采用4个校验位求其偶校验方式的海明码。
解:D7.D6.D5.D4.D3.D2.D1 = 01101001,根据公式

验算

三、循环冗余校验码
循环冗余效验码广泛应用于数据通信领域和磁介质存储系统中。他利用生成多项式为k个数据位产生r个校验码位来进行编码,其编码长度为k+r。CRC的代码格式为:

由此可知,循环冗余校验码是由两部分组成,左边的为信息码(数据),右边的为校验码。若信息码占k位,则冗余校验码就占n-k位。其中,n位CRC码的字长,所以又称为(n,k)码。效验码是由信息码产生的,效验码位数越长,改代码的校验能力就越强。在求CRC编码时,采用的是模2运算。
1.模2运算
先提前介绍一下模2加减运算的规则是:按位运算,不发生错位和进位,如下
0+0=0 1+0=1 0+1=1 1+1=0
0-0=0 1-0=1 0-1=1 1-1=0
在计算循环冗余校验码之前,我们先获得一些必要条件。
信息码,生成多项式,校验位,多项式对应的二进制数,余数。
信息码就是数据,生成多项式就是除数。有什么作用呢,信息码加校验码莫2除以除数为0,则表示信息传输无误。这就是循环冗余校验码的校验方式。所以生成多项式一般由数据的发送方和接收方同时定义。根据生成多项式计算校验位以及对应的二进制数。如何根据多项式计算校验位,多项式的最高次幂就是校验位位数。对应的二进制数(除数)为多项式系数相加。
2.信息码和多项式
例:设数据(信息码)为101001,生成多项式为G(X)= X^3+X^2+1,求CRC代码;
解:根据信息码和生成多项式可得
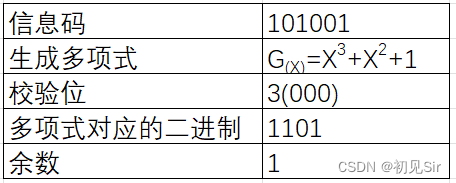
3.校验位
校验位为多项式最高次幂,可得知校验位为3位,用000填充。
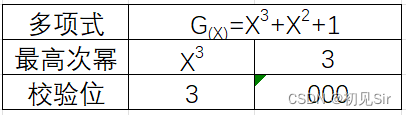
4.多项式对应的2进制
多项式对应的二进制为每一项的系数,没有的则为0,二进制系数为110+1,则除数为1101

将信息码和校验位相拼凑得出被除数为101001000

将被除数(101001000)和除数(1101)进行模2运算

得到余数为1,余数就是最终校验位,则最终的CRC代码为101001001
验算一边的话就是将CRC代码除以多项式对应的二进制,最终结果为0,
且可以将结果翻译为对应的十进制查看错误位置,例如。余数为101,则错误位数在第五位。
总结
以上就是学习的结果,关于循环冗余校验中“冗余”,实际传输的数据中包含不表达信息的冗余位。是进行检验的代价,提供检验的可行性。“循环”检验过程中数据在计算机中重复计算检验的过程,也就是循环的由来。
























 1868
1868

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










