单调栈讲解

目录

MT3042这项目我小码哥投了

MT3039山脉

MT3040矩形覆盖

MT3041多项式变换求值

---

        

        

单调栈不可怕，记住一句话：找右边(或左边)第一个小于或大于的数，用单调栈

        

        

 单调栈引入

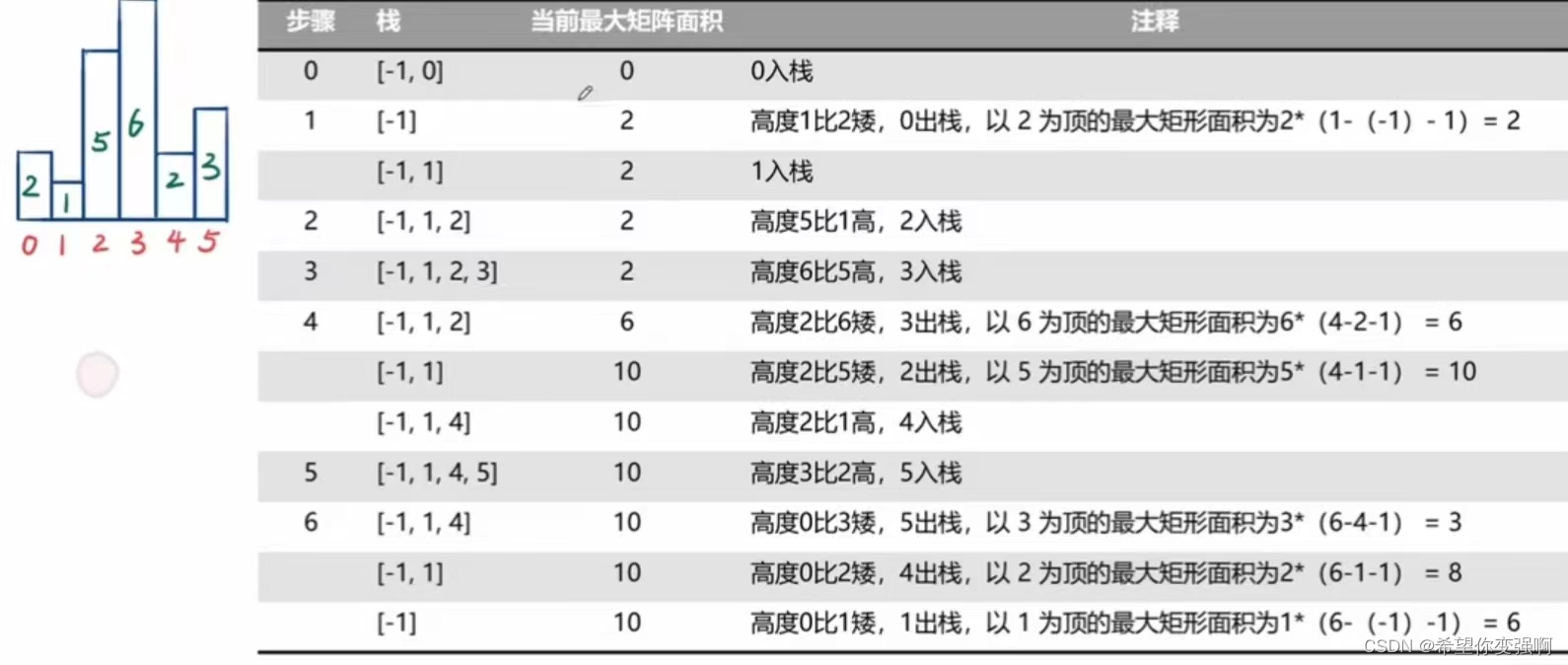
我们需要维护一个递增的单调栈，同时要给下标入栈，而不是元素入栈。

给i位置入栈的时候，发现右指针i+1位置元素一定小，而左指针i-1位置元素也一定小，所以当前i位置元素出栈对应的答案为（(i+1)指向的下标的元素 - (i-1)指向的下标的元素 - 1）*a[i的下标]

元素：2  1  5  6  2  3  

下标：0  1  2  3  4  5

2入栈

栈：0

1入栈，发现不单调，0下标需要出栈，又因为0已经最左边位置了，所以0的左边应该是-1下标：更新答案{1-（-1）-1}*a[0]=2

栈：1

5入栈

栈：1,2

6入栈

栈：1,2,3

2入栈，发现不单调，3下标需要出栈，所以更新答案：{4-2-1}*a[3]=6，2下标也需要出栈，更新答案：{4-1-1}*a[2]=10

栈：1,4

3入栈

栈：1,4,5

开始出栈：

5下标先出栈，更新答案：{6-4-1}*a[5]=3，4下标再出栈，更新答案：{6-3-1}*a[4]=4，1下标再出栈，更新答案：{6-(-1)-1}*a[1]=6

综上：答案为10.

下面是图解： 

        

        

MT3042这项目我小码哥投了

其实这个是一个二维单调栈的用法，再进一步说就是上面的题的二维形态。

请看下图： 

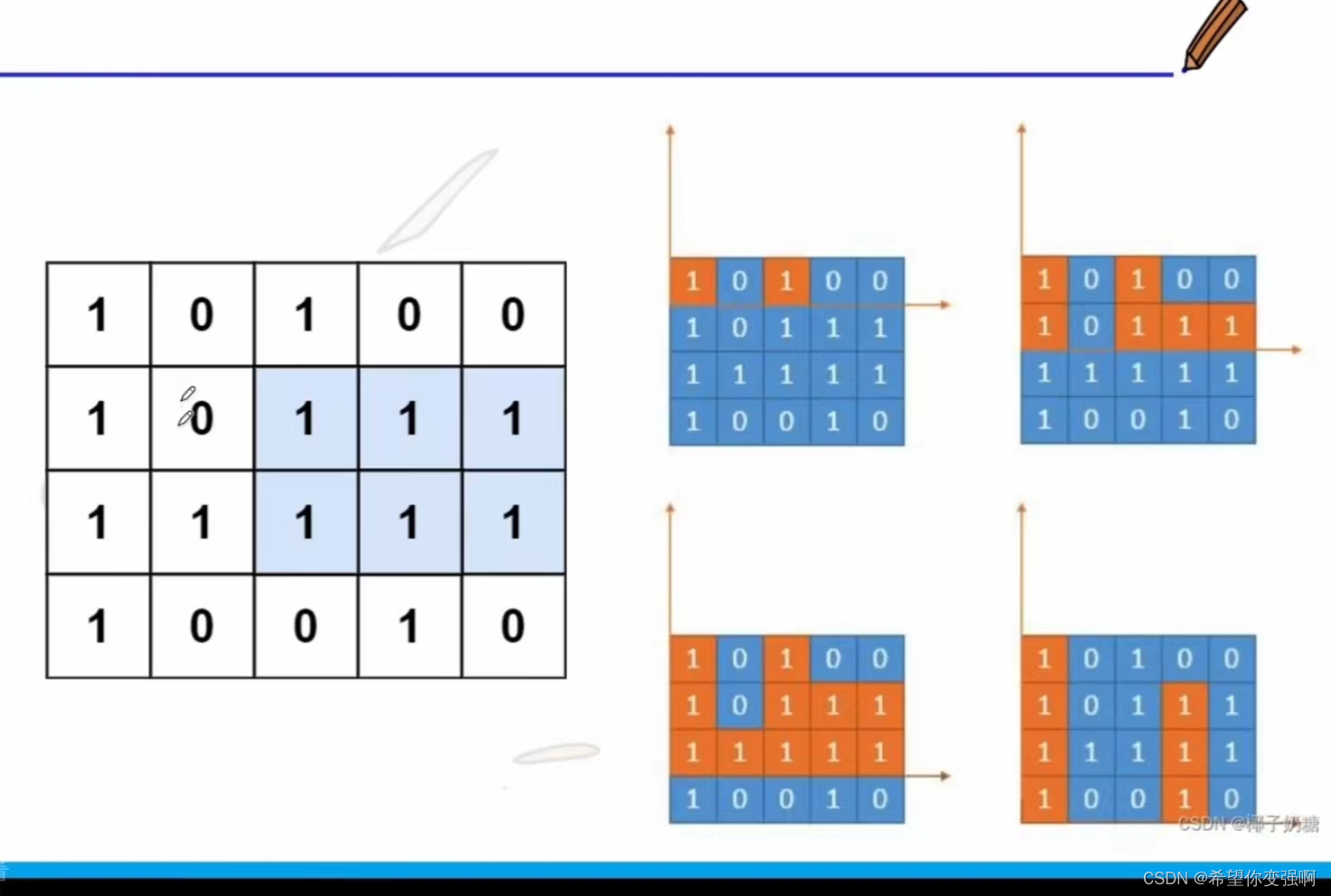
加入现在是这种状态，那么我们可以从第一行开始跑一次一维单调栈，获得一个ans。

然后从第二行跑一次一维单调栈，再获得一个ans，不断的重复，获得最大的ans即可。 

#include <bits/stdc++.h>
using namespace std;
const int N=1e3+5;
int n,m,a[N][N],ans;
char ch;
int maxx(int x){
	int ret=0;
	stack<int>s;
	s.push(0);//在左边添加一个0下标
	for(int i=1;i<=m+1;i++){
		while(a[x][i]<a[x][s.top()]){//更小元素来了，栈不单调就要有元素出栈
			int h=a[x][s.top()];//每出栈一个元素就获得一个矩形高度
			s.pop();
			int w=i-s.top()-1;求底边：i是右边界，s.top()是左边界
			ret=max(ret,w*h);
		}
		s.push(i);//直到栈单调后才把新元素入栈
	}
	return ret;
}
int main(){
	cin>>n>>m;
	for(int i=1;i<=n;i++){
		for(int j=1;j<=m;j++){
			cin>>ch;
			if(ch=='G')a[i][j]=1;
		}
	}
	for(int i=1;i<=n;i++){
		for(int j=1;j<=m;j++){
			if(a[i][j])a[i][j]+=a[i-1][j];
		}
	}
	for(int i=1;i<=n;i++){
		ans=max(ans,maxx(i));
	}
	cout<<ans*10;
}

        

        

MT3039山脉

单调栈。为什么能想到单调栈？因为要求的是总数，而我们把往后看转化成向左看，即在每个元素入栈的时候看一下左边有几个元素可以看到它，这样做求得的总数是不会变的。

所以我们需要一个单减的单调栈。

新元素进栈时候不会改变单调性就直接进栈，同时统计有几个元素可以看到它（栈里有几个元素）。如果会改变单调性，就把栈中的元素一个一个出栈。统计答案，新元素入栈。

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
ll n,num,sum;
stack<int>sk;
int main(){
	cin>>n;
	for(int i=1;i<=n;i++){
		scanf("%lld",&num);
		while(!sk.empty()&&sk.top()<=num) sk.pop();
		sum+=sk.size();
		sk.push(num);
		
	}
	cout<<sum;
}

        

        

MT3040矩形覆盖

首先就是观察规律：

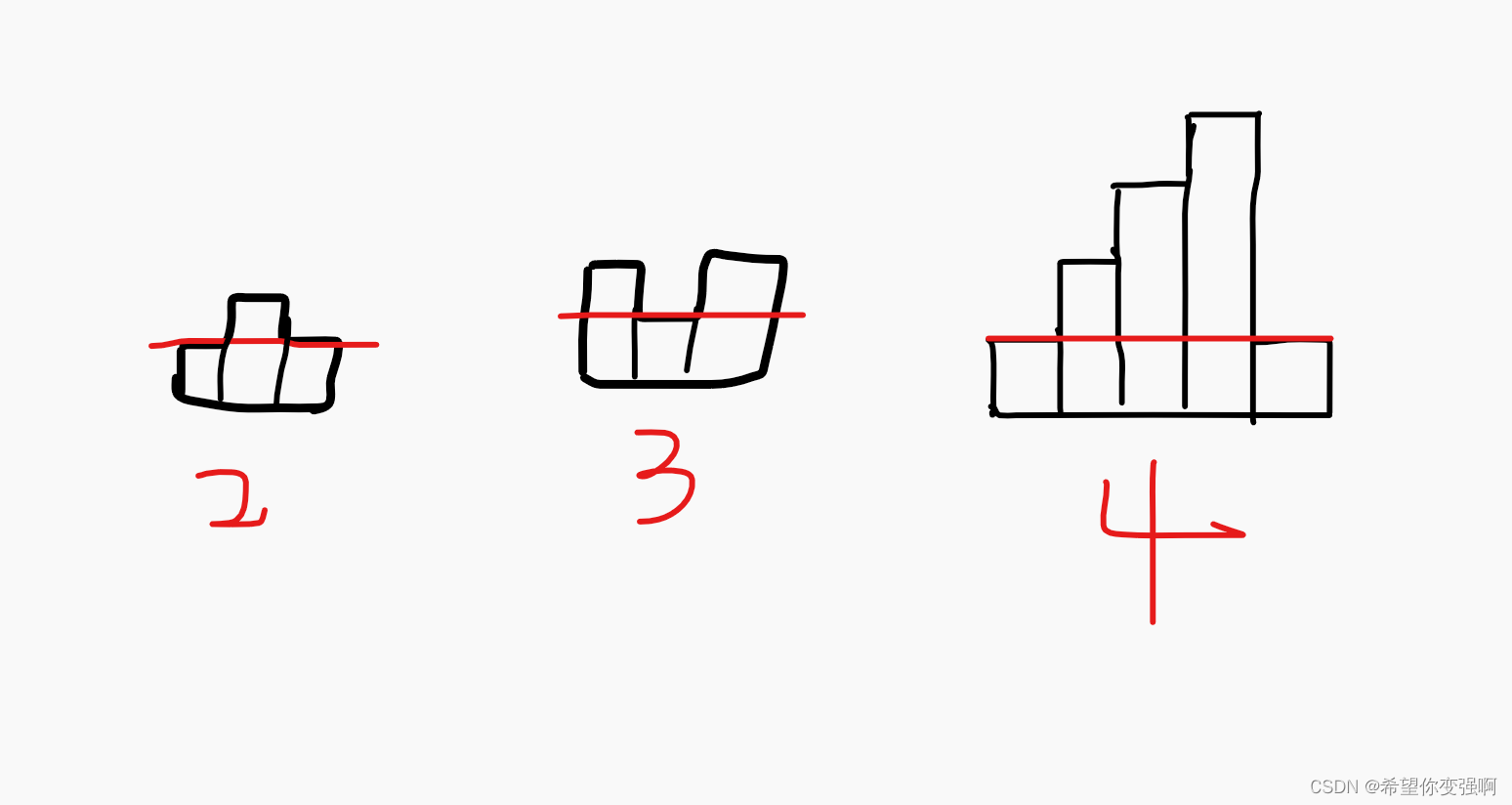
根据2,3情况。

我们发现如果左右有同高度且中间是凸出的矩形条，最好就要把这个红色横线下面的大矩形给贴一下。

而对于左右有同高度且中间有凹下的矩形条，你按不按照这个红色横线去贴，答案都不变。

然后用4情况来进行验证，发现确实是这样的。

那么如何统计答案呢？第2种情况下一定会少贴一次，那么如果有更多同高度的矩形条，就会少贴更多次。我们只需要统计少贴多少次就行。

所以我们需要一个单调增加的栈。

新元素进栈不会改变单调性就直接入栈

新元素入栈会改变单调性，就把栈里面的元素进行出栈，直到左边的同高度的元素也出栈，然后ans++，表示这里可以少贴一次。新元素入栈。

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
int n,ans,d,w;
stack<int>sk;
int main(){
	cin>>n;
	for(int i=1;i<=n;i++){
		cin>>d>>w;
		while(!sk.empty()&&w<=sk.top()){
			if(sk.top()==w) ans++;
		sk.pop();}
		sk.push(w);
	}
	cout<<n-ans;
}

        

        

MT3041多项式变换求值

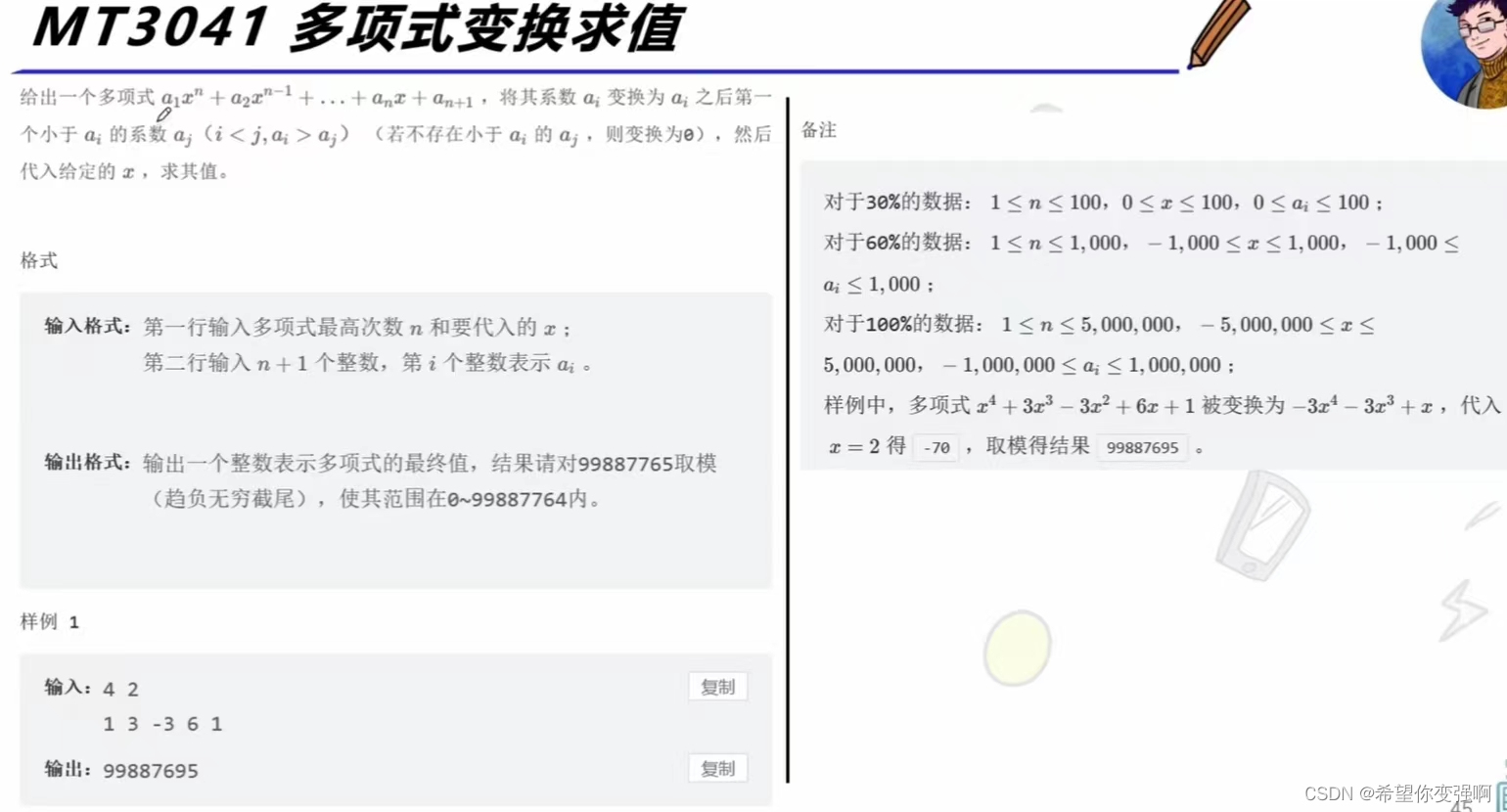
我们要维护一个单调递增的单调栈，在新来的元素比栈顶元素小的时候，栈顶元素出栈，并更新，直到新元素可以入栈为止。

唯一要注意的就是负数取模了，要现加上去mod再取模。 

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int mod=99887765,N=5e6+5;
stack<int>st;
ll ans;
int n,x,a[N],b[N];
int main(){
	cin>>n>>x;
	for(int i=1;i<=n+1;i++){
		cin>>a[i];
		while(!st.empty()&&a[i]<a[st.top()]){
			b[st.top()]=a[i];
			st.pop();
		}
		st.push(i);
	}
	for(int i=1;i<=n+1;i++){
		ans=ans*x+b[i];
		ans=(ans%mod+mod)%mod;//注意负数是如何取模的
	}
	cout<<ans;
}