OpenHarmony实战开发-如何通过Function Flow编程模型和FFRT实现并行编程。

最新推荐文章于 2025-02-12 21:06:28 发布

不入流HarmonyOS开发

最新推荐文章于 2025-02-12 21:06:28 发布

阅读量729

点赞数 3

分类专栏： HarmonyOS OpenHarmony 鸿蒙文章标签： harmonyos OpenHarmony 鸿蒙系统 HarmonyOS 华为鸿蒙鸿蒙工程师

本文链接：https://blog.csdn.net/m0_70749039/article/details/138921393

版权

场景介绍

Function Flow编程模型是一种基于任务和数据驱动的并发编程模型，允许开发者通过任务及其依赖关系描述的方式进行应用开发。FFRT（Function Flow运行时）是支持Function Flow编程模型的软件运行时库，用于调度执行开发者基于Function Flow编程模型开发的应用。通过Function Flow编程模型和FFRT，开发者可专注于应用功能开发，由FFRT在运行时根据任务依赖状态和可用执行资源自动并发调度和执行任务。

本文用于指导开发者基于Function Flow编程模型和FFRT实现并行编程。

接口说明

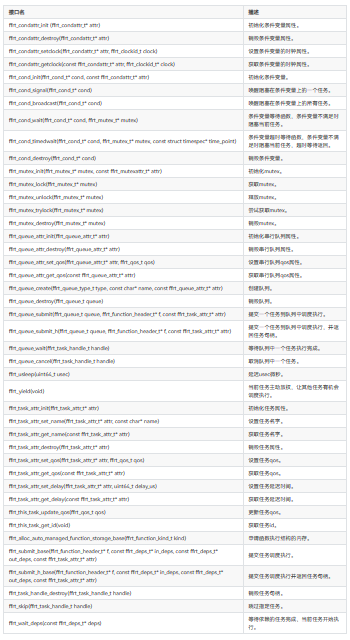
在这里插入图片描述

函数介绍

任务管理
ffrt_submit_base

该接口为ffrt动态库的导出接口，基于此可以封装出C API ffrt_submit，满足二进制兼容。

声明

const int ffrt_auto_managed_function_storage_size = 64 + sizeof(ffrt_function_header_t);
typedef enum {
   
    ffrt_function_kind_general,
    ffrt_function_kind_queue
} ffrt_function_kind_t;

void* ffrt_alloc_auto_managed_function_storage_base(ffrt_function_kind_t kind);

typedef void(*ffrt_function_t)(void*);
typedef struct {
   
    ffrt_function_t exec;
    ffrt_function_t destroy;
    uint64_t reserve[2];
} ffrt_function_header_t;

void ffrt_submit_base(ffrt_function_header_t* func, const ffrt_deps_t* in_deps, const ffrt_deps_t* out_deps, const ffrt_task_attr_t* attr);

参数
kind

function子类型，用于优化内部数据结构，默认使用ffrt_function_kind_general类型。

func

CPU Function的指针，该指针执行的数据结构，按照ffrt_function_header_t定义的描述了该CPUTask如何执行和销毁的函数指针，FFRT通过这两个函数指针完成Task的执行和销毁。

in_deps

该参数是可选的。
该参数用于描述该任务的输入依赖，FFRT 通过数据的虚拟地址作为数据的Signature 来建立依赖。

out_deps

该参数是可选的。
该参数用于描述该任务的输出依赖。
注意：该依赖值本质上是一个数值，ffrt没办法区分该值是合理的还是不合理的，会假定输入的值是合理的进行处理；但不建议采用NULL，1, 2等值来建立依赖关系，建议采用实际的内存地址，因为前者使用不当会建立起不必要的依赖，影响并发。

attr

该参数是可选的。
该参数用于描述Task 的属性，比如qos 等，详见 ffrt_task_attr_t章节。

返回值

不涉及。

描述

建议用户对ffrt_submit_base进行封装后调用，具体可参考样例。
ffrt_submit_base作为底层能力，使用时需要满足以下限制：
ffrt_submit_base入参中的func指针只能通过
ffrt_alloc_auto_managed_function_storage_base申请，且二者的调用需一一对应。
ffrt_alloc_auto_managed_function_storage_base申请的内存为ffrt_auto_managed_function_storage_size字节，其生命周期归ffrt管理，在该task结束时，由FFRT自动释放，用户无需释放。
ffrt_function_header_t 中定义了两个函数指针：
exec：用于描述该Task如何被执行，当FFRT需要执行该Task时由FFRT调用。
destroy：用于描述该Task如何被销毁，当FFRT需要销毁该Task时由FFRT调用。

样例

template<class T>
struct function {
   
    template<class CT>
    function(ffrt_function_header_t h, CT&& c) : header(h), closure(std::forward<CT>(c)) {
   }
    ffrt_function_header_t header;
    T closure;
};

template<class T>
void exec_function_wrapper(void* t)
{
   
    auto f = (function<std::decay_t<T>>*)t;
    f->closure();
}

template<class T>
void destroy_function_wrapper(void* t)
{
   
    auto f = (function<std::decay_t<T>>*)t;
    f->closure = nullptr;
}

template<class T>
inline ffrt_function_header_t* create_function_wrapper(T&& func)
{
   
    using function_type = function<std::decay_t<T>>;
    static_assert(sizeof(function_type) <= ffrt_auto_managed_function_storage_size,
        "size of function must be less than ffrt_auto_managed_function_storage_size");

    auto p = ffrt_alloc_auto_managed_function_storage_base(ffrt_function_kind_general);
    auto f = new (p) function_type(
        {
   exec_function_wrapper<T>, destroy_function_wrapper<T>},
        std::forward<T>(func));
    return (ffrt_function_header_t*)f;
}

static inline void submit(std::function<void()>&& func)
{
   
    return ffrt_submit_base(create_function_wrapper(std::move(func)), NULL, NULL, NULL);
}

ffrt_wait

同步等待，与ffrt_submit_base 配合使用。 * 等待指定的数据被生产完成，或等待当前任务的所有子任务完成，在不满足条件之前，当前的执行上下文被suspend，在满足条件后恢复执行。

声明

void ffrt_wait_deps(ffrt_deps_t* deps);
void ffrt_wait();

参数
deps

需要等待被生产完成的数据的虚拟地址，这些地址可能作为某些任务在submit时的out_deps，该依赖的生成见ffrt_deps_t章节，空指针表示无依赖。

返回值

不涉及。

描述

ffrt_wait_deps(deps) 用于等待deps指代的数据被生产完成才能执行后面的代码。
ffrt_wait()用于等待当前上下文提交的所有子任务（注意：不包括孙任务和下级子任务）都完成才能执行后面的代码。
该接口支持在FFRT task内部调用，也支持在FFRT task 外部调用。
在FFRT task 外部调用的wait 是OS 能够感知的等待，相对于FFRTtask 内部调用的wait 是更加昂贵的，因此我们希望尽可能让更多的wait 发生在FFRT task 内部，而不是FFRT task外部。

样例
recursive fibonacci

串行版的fibonacci 可以实现为：

#include <stdio.h>

void fib(int x, int* y) {
   
    if (x <= 1) {
   
        *y = x;
    } else {
   
        int y1, y2;
        fib(x - 1, &y1);
        fib(x - 2, &y2);
        *y = y1 + y2;
    }
}
int main(int narg, char** argv)
{
   
    int r;
    fib(10, &r);
    printf("fibonacci 10: %d\n", r);
    return 0;
}

若要使用 FFRT 实现并行（注，对于单纯的fibonacci，单个 Task 的计算量极小，不具有并行加速的意义，但这种调用pattern 对并行编程模型的灵活性考验是非常高的），其中1种可行的实现为：

#include <stdio.h>
#include "ffrt.h"  //包含所有ffrt涉及的头文件

typedef struct {
   
    int x;
    int* y;
} fib_ffrt_s;

typedef struct {
   
    ffrt_function_header_t header;
    ffrt_function_t func;
    ffrt_function_t after_func;
    void* arg;
} c_function;

static void ffrt_exec_function_wrapper(void* t)
{
   
    c_function* f = (c_function*)t;
    if (f->func) {
   
        f->func(f->arg);
    }
}

static void ffrt_destroy_function_wrapper(void* t)
{
   
    c_function* f = (c_function*)t;
    if (f->after_func) {
   
        f->after_func(f->arg);
    }
}

#define FFRT_STATIC_ASSERT(cond, msg) int x(int static_assertion_##msg[(cond) ? 1 : -1])
static inline ffrt_function_header_t* ffrt_create_function_wrapper(const ffrt_function_t func,
    const ffrt_function_t after_func, void* arg)
{
   
    FFRT_STATIC_ASSERT(sizeof(c_function) <= ffrt_auto_managed_function_storage_size,
        size_of_function_must_be_less_than_ffrt_auto_managed_function_storage_size);
    c_function* f = (c_function*)ffrt_alloc_auto_managed_function_storage_base(ffrt_function_kind_general);
    f->header.exec = ffrt_exec_function_wrapper;
    f->header.destroy = ffrt_destroy_function_wrapper;
    f->func = func;
    f->after_func = after_func;
    f->arg = arg;
    return (ffrt_function_header_t*)f;
}

static inline void ffrt_submit_c(ffrt_function_t func, const ffrt_function_t after_func,
    void* arg, const ffrt_deps_t* in_deps, const ffrt_deps_t* out_deps, const ffrt_task_attr_t* attr)
{
   
    ffrt_submit_base(ffrt_create_function_wrapper(func, after_func, arg), in_deps, out_deps, attr);
}

#define ffrt_deps_define(name, dep1, ...) const void* __v_##name[] = {dep1, ##__VA_ARGS__}; \
    ffrt_deps_t name = {
   sizeof(__v_##name) / sizeof(void*), __v_##name}

void fib_ffrt(void* arg)
{
   
    fib_ffrt_s* p = (fib_ffrt_s*)arg;
    int x = p->x;
    int* y = p->y;

    if (x <= 1) {
   
        *y = x;
    } else {
   
        int y1, y2;
        fib_ffrt_s s1 = {
   x - 1, &y1};
        fib_ffrt_s s2 = {
   x - 2, &y2};
        ffrt_deps_define(dx, &x);
        ffrt_deps_define(dy1, &y1);
        ffrt_deps_define(dy2, &y2);
        ffrt_deps_define(dy12, &y1, &y2);
        ffrt_submit_c(fib_ffrt, NULL, &s1, &dx, &dy1, NULL);
        ffrt_submit_c(fib_ffrt, NULL, &s2, &dx, &dy2, NULL);
        ffrt_wait_deps(&dy12);
        *y = y1 + y2;
    }
}

int main(int narg, char** argv)
{
   
    int r;
    fib_ffrt_s s = {
   10, &r};
    ffrt_deps_define(dr, &r);
    ffrt_submit_c(fib_ffrt, NULL, &s, NULL, &dr, NULL);
    ffrt_wait_deps(&dr);
    printf("fibonacci 10: %d\n", r);
    return 0;
}

解析：

1.将fibonacci (x-1)和fibonacci (x-2) 作为2个Task 提交给FFRT，在两个Task 完成之后将结果累加；

2.虽然单个Task 只能拆分成2个SubTask 但是子Task 可以继续拆分，因此，整个计算图的并行度是非常高的，Task 之间在FFRT 内部形成了一颗调用树；

以上实现，因为需要用户显式管理数据生命周期和函数入参打包两个因素，所以使得代码实现异常复杂。

ffrt_deps_t

C API中对依赖数组的抽象，逻辑上等同于C++ API中的std::vector<void*>

声明

typedef enum {
   
    ffrt_dependence_data,
    ffrt_dependence_task,
} ffrt_dependence_type_t;

typedef struct {
   
    ffrt_dependence_type_t type;
    const void* ptr;
} ffrt_dependence_t;

typedef struct {
   
    uint32_t len;
    const ffrt_dependence_t* items;
} ffrt_deps_t;

参数
len

所依赖的Signature的个数，取值大于等于0。

item

len个Signature的起始地址指针。

type

当前依赖为数据依赖还是任务依赖。

ptr

所依赖对应Signature内容的实际地址。

返回值

不涉及。

描述

item为len个Signature的起始指针，该指针可以指向堆空间，也可以指向栈空间，但是要求分配的空间大于等于len *
sizeof(ffrt_dependence_t)。

样例

创建数据依赖或者任务依赖：

// 创建数据依赖的ffrt_deps_t
int x = 0;
const std::vector<ffrt_dependence_t> in_deps = {
   {
   ffrt_dependence_data, &x}};
ffrt_deps_t in{
   static_cast<uint32_t>(in_deps.size()), in_deps.data()};

// 提交某个返回handle任务
ffrt_task_handle_t task = ffrt_submit_h_base(
        ffrt_create_function_wrapper(OnePlusForTest, NULL, &a), NULL, NULL, &attr);
// 创建任务依赖的ffrt_deps_t
const std::vector<ffrt_dependence_t> wait_deps = {
   {
   ffrt_dependence_task, task}};
ffrt_deps_t wait{
   static_cast

最低0.47元/天解锁文章