最近两篇文章呢,我们来学习一下字符串匹配算法:
字符串匹配算法是用于在一个主串中寻找一个模式串的出现位置的算法。具体来说,它解决的问题是在一个较长的字符串(主串)中查找一个较短的字符串(模式串)是否存在,并返回模式串在主串中的起始位置或所有匹配的位置。
字符串匹配算法呢其实有好几个呢,这里我们主要学习两个——BF算法和KMP算法。
其中KMP算法是需要大家重点掌握的一种算法,面试过程是有可能会被考到的!
那本篇文章我们先来学习一下BF算法
BF算法
1. 算法思想
BF算法,即暴力(Brute Force)算法,是普通的模式匹配算法
BF算法,即暴力(Brute Force)算法,是普通的模式匹配算法,BF算法的思想就是将目标串S的第一个字符与模式串T的第一个字符进行匹配,若相等,则继续比较S的第二个字符和 T的第二个字符;若不相等,则比较S的第二个字符和T的第一个字符,依次比较下去,直到得出最后的匹配结果。BF算法是一种蛮力算法。
(百度百科)
上面这段话可能不是特别好理解,我来给大家解释一下:
其实思想是很简单的:
首先从两个字符串的第一个字符开始比较(依次比较每对字符),如果相等,就继续比下一对字符,一直往后走;如果遇到某一对字符不再相等,这时让子串回到第一个字符,主串回到上一次匹配的起始位置的下一个字符,然后再开始两两进行比较,重复上述操作,最终得到匹配结果。
2. 图解
单凭上面的概念,大家可能还不是特别理解,下面我们通过一个具体的例子再来带大家理解一下这个算法:
假定我们给出字符串 ”ababcabcdabcde”作为主串, 然后给出子串: ”abcd”,现在我们需要查找子串是否在主串中出现,出现则返回主串中的第一个匹配的下标,失败返回-1
那么整个过程是这样的:
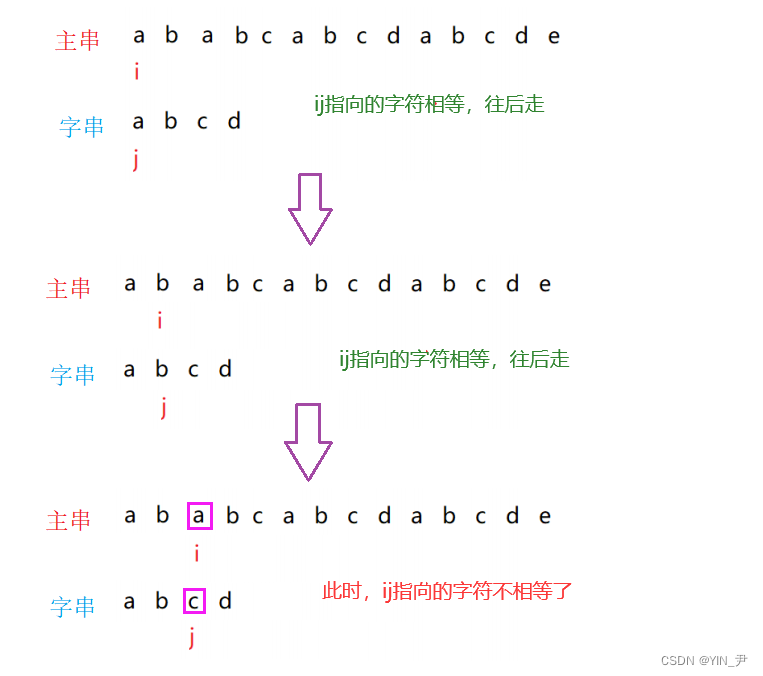
首先ij都从第一个字符开始,两两一对,进行比较,如果相等,i++,j++往后走
一直往后走到ij都指向第3个字符的时候,我们发现此时两个字符不相等了。
那就意味着从主串的第一个字符开始往后匹配是匹配失败的!
那怎么办?
🆗,那就从主串的下一个字符(第二个)往后重新匹配子串。
所以:
我们让j回退到子串的起始位置(因为我们要重新匹配),i回退到主串上一次匹配起始位置(下标0位置)的下一个位置(即下标1位置)
重新开始匹配
那这一次上来i和j指向的字符就不相等
怎么办?重复上面的操作
j回到子串起始位置,i回到上一次匹配的起始位置的下一个位置(下标2的位置)
再次重新开始匹配
那这一次我们发现前三个字符都匹配成功了,第四个没有匹配上,所以从下标2这个位置开始也匹配失败
那再让j回到子串起始位置(j=0),i回到主串上一次匹配的起始位置的下一个位置(下标3的位置)
那同时这里大家思考一下,我们待会写代码的时候怎么计算i回退的位置?
j很简单,j=0就回去了。
那i呢?
🆗,很简单,i=i-j+1就可以了
因为ij是同步走的,而每次匹配j都是从0开始的,所以它们一共走了j步,那i=i-j的话i就回到上一次匹配的起始位置了,再+1,就是回到主串上一次匹配的起始位置的下一个位置
那我们继续,再进行下一轮匹配
这次开始是这样的
那上来ij指向的字符就不相等
下一轮
上来直接不相等,下一轮
这一轮匹配的话
最终把子串遍历完了(j==sub.length())。
那就说明匹配成功了,那我们要返回子串在主串中出现的起始位置(第一个匹配的下标),那这个下标是几啊?
🆗,就是此时i-j的值
如果是其它情况:
那就说明匹配失败啊,主串里面不包含这个子串。
我们返回一个-1。
那相信现在大家应该比较清晰的理解这个算法了。
时间复杂度分析:
最坏为O(m*n); m是主串长度,n是子串长度
我们来写一下代码:
3. 代码实现
那思路理清之后,写代码还是很简单的:
🆗,就搞定了,代码比较简单,就不过多解释了
我们来测试一下:
没问题!
4. 源码
#include <iostream>
using namespace std;
#include <string>
int BF(const string& str, const string& sub)
{
if (str.empty() || sub.empty())
return -1;
int i = 0;
int j = 0;
while (i < str.size() && j < sub.size())
{
if (str[i] == sub[j])
{
i++;
j++;
}
else
{
i = i - j + 1;
j = 0;
}
}
if (j == sub.size())
{
return i - j;
}
return -1;
}
int main()
{
cout << BF("ababcabcdabcde", "abcd") << endl;
cout << BF("ababcabcdabcde", "abcdef") << endl;
cout << BF("ababcabcdabcde", "ab") << endl;
return 0;
}








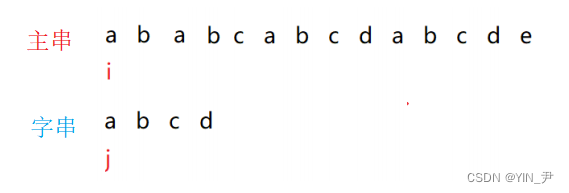





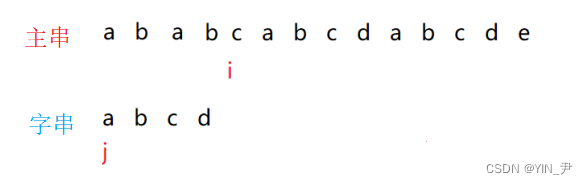
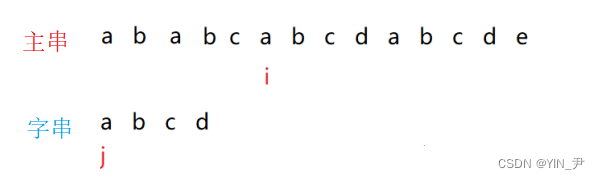




















 5185
5185

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










