【空间光-光纤耦合技术04】单模光纤特性分析（上）

本部分的学习参考柯熙政老师的《无限光通信中的空间光——光纤耦合技术》及欧攀老师的《高等光学仿真（MATLAB版）》，为自学笔记，博客末尾附上了在学习过程中参考的博客内容。

        在单模光纤中，常见的LP模式包括LP01、LP11等。其中，LP01模式是最基本的模式，也是单模光纤在单模工作波长范围内唯一能够传导的模式。随着波长的变化，其他高阶模式（如LP11）可能会逐渐截止，无法被光纤传导。

单模光纤的特征方程

        LP01模也称为光纤中的基模，根据其本征方程及V、U和W的相互关系可以在matlab中求解（求解方法已经在之前的内容中给出）：

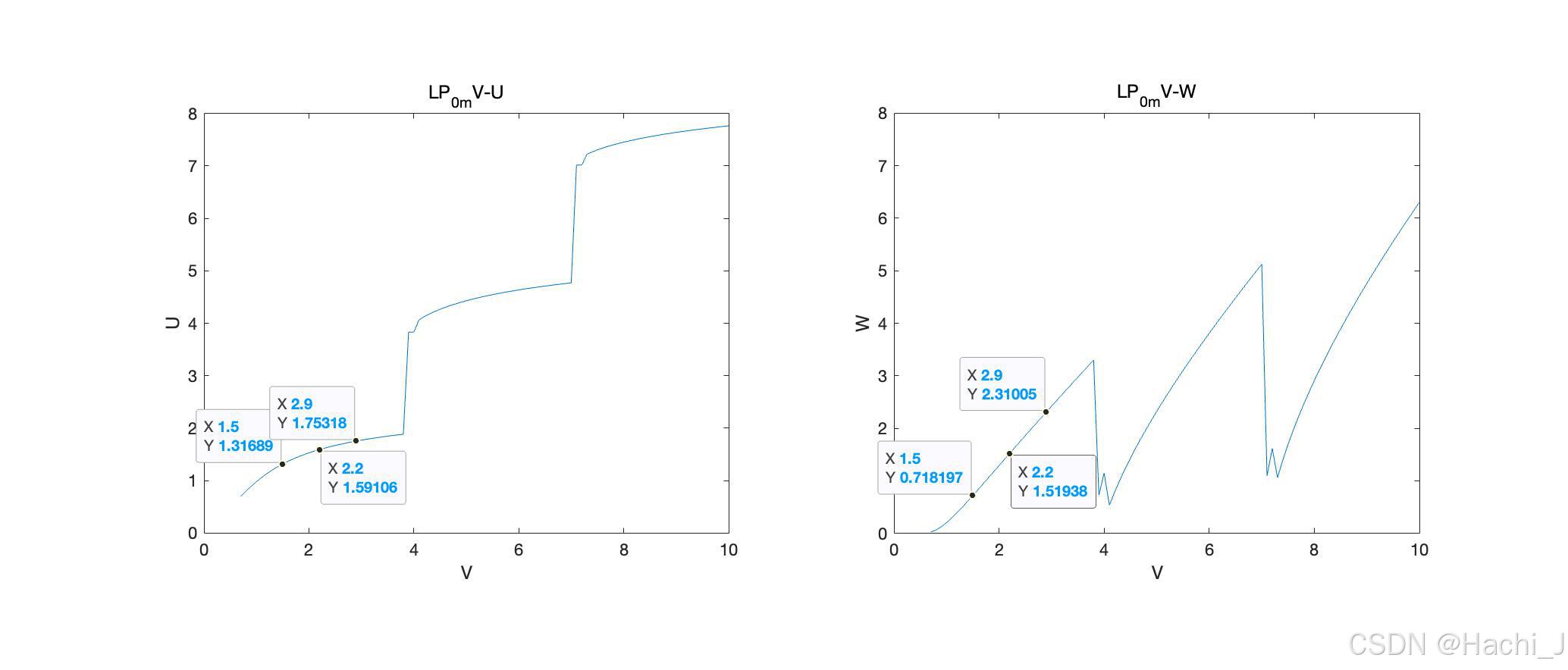
单模光纤的一维模场分布

        单模光纤中LP01模在纤芯区和包层区的归一化电场分布为：

        利用上述关系式，即可得出归一化的LP01模在纤芯区和包层区的电场分布曲线，如图画出了上图取的三种不同参数的LP01模的光纤一维分布电场图、光强图（蓝红黄对应V值不断增大）：

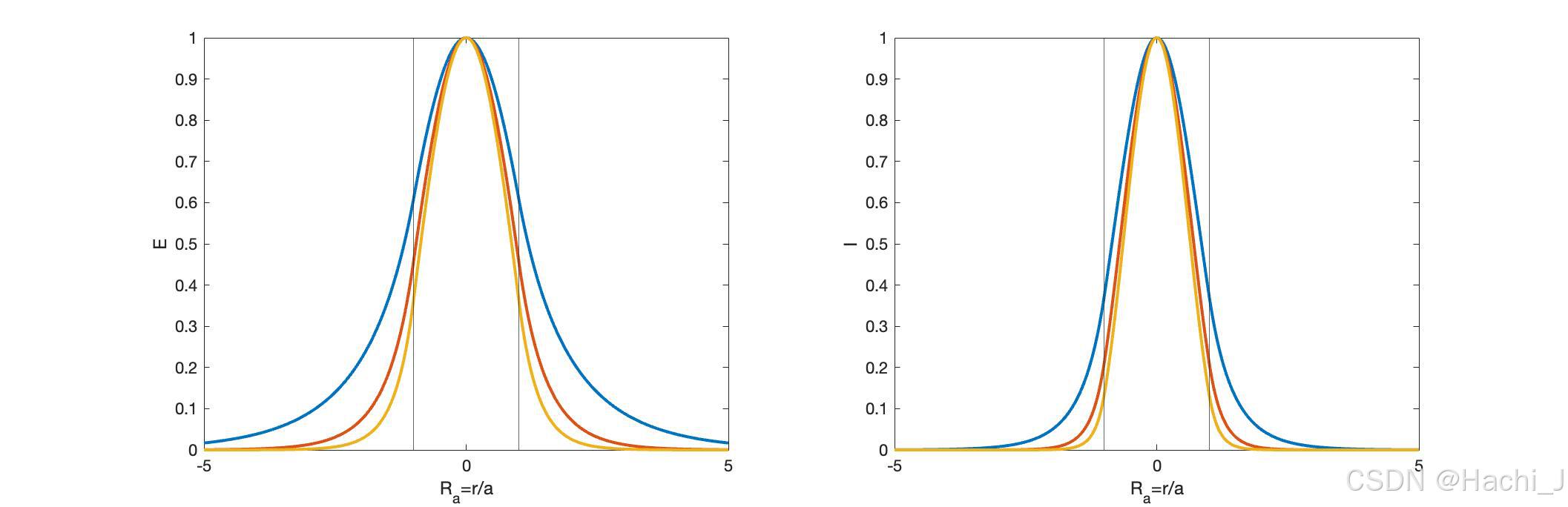
        从图中可以看出随着V的逐渐增大，单模光纤中LP01模的模场分布更加集中在纤芯（图中两线之间的区域）内。但是，导波模场在包层区的衰减快慢、防止高阶模出现、防止基模场将延伸进入包层介质等问题需要根据实际情况对V的取值进行权重。

        核心代码如下所示：

Ra1 = -1:0.01:1;   % 纤芯
Ra2 = [-5:0.01:-1];   % 左包层
Ra3 = [1:0.01:5];   % 右包层

E1 = zeros(length (V) , length (Ra1));
E2 = zeros(length (V) , length (Ra2));
E3 = zeros(length (V) , length (Ra3));

for i = 1: length (V)
    E1(i,:) = besselj(0,U(i) *Ra1);
    E2(i,:) = besselj(0,U(i)) .*besselk(0, W(i) .*abs(Ra2)) ./besselk(0,W(i));
    E3(i,:) = besselj(0,U(i)) .*besselk(0, W(i) .*abs(Ra3)) ./besselk(0,W(i));
    I1(i,:) = E1(i,:).^2;
    I2(i,:) = E2(i,:).^2;
    I3(i,:) = E3(i,:).^2;
end

单模光纤的二维模场分布

        二维图像则是将平面拆分为网格然后带入式子中计算：

% 网格设定及计算
x = linspace(-Rx, Rx, Npoint);
y = linspace(-Ry, Ry, Npoint);
X = meshgrid (x, y);
Y = meshgrid (y, x);
Y = Y';
R = sqrt (X.^2 + Y.^2);

% 单模光纤纤芯和包层中的电场分量计算
E1 = besselj(0,U*R) ;
E2 = besselj(0,0) .*besselk(0,W.*R) ./besselk(0,W);
E = E1;
pos = find(R>=1);
E(pos) = E2(pos);

% 单模光纤纤芯和包层中的电场分量的二维强度作图
imagesc(x, y, E);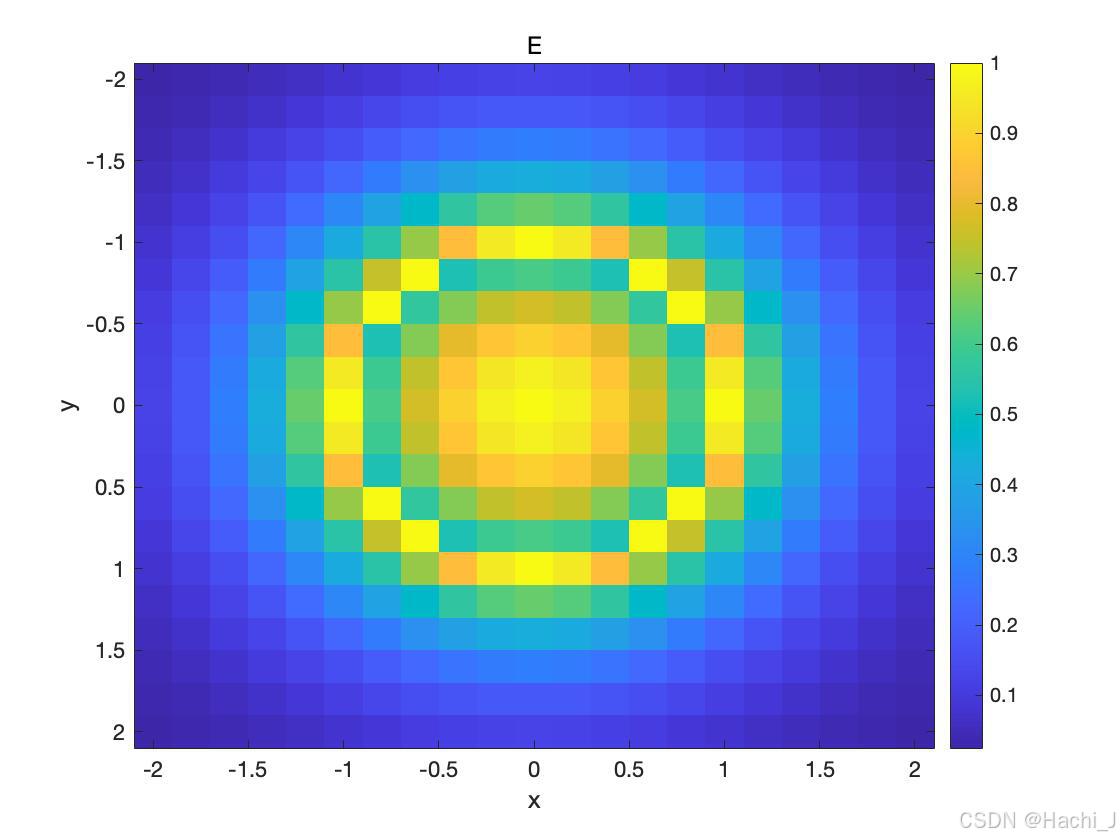

        使用contour()函数可以绘制等高线图，效果如下图所示：

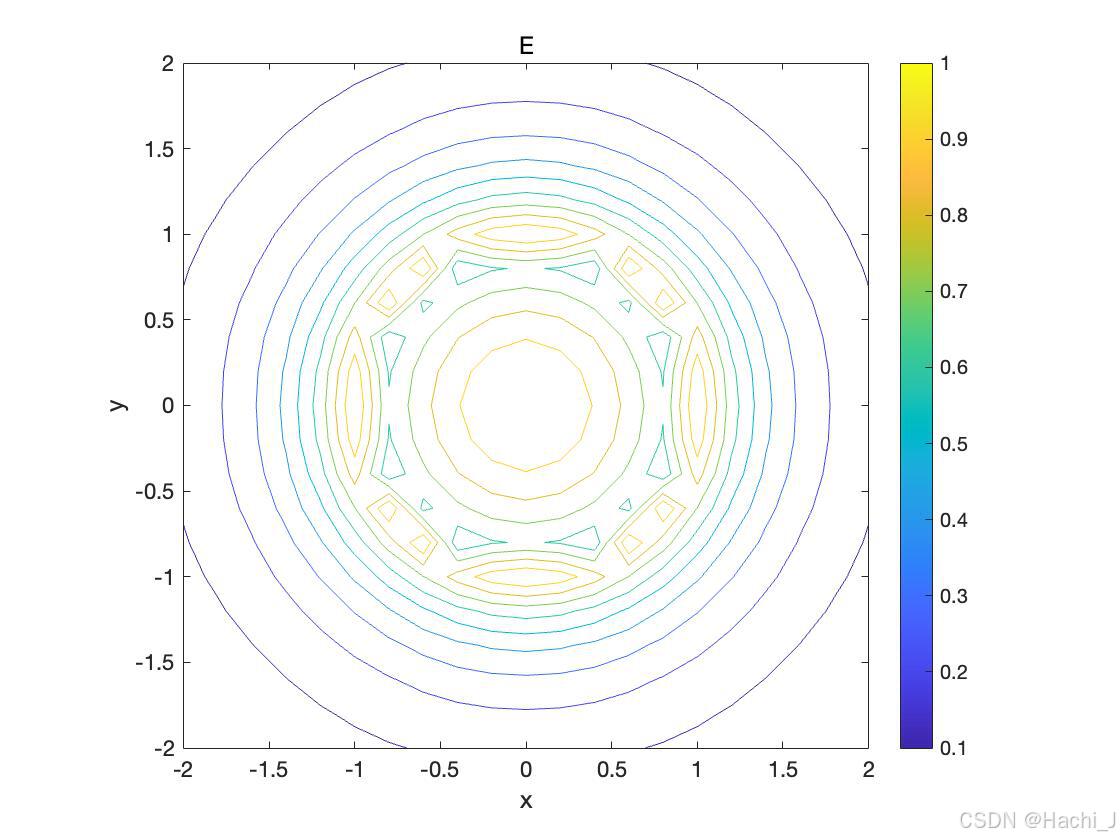
        在此基础上利用以下函数可以绘制等高线上的剃度矢量：

[px, py] = gradient(E);
contour (X, Y, E)
hold on
quiver (X, Y, px, py);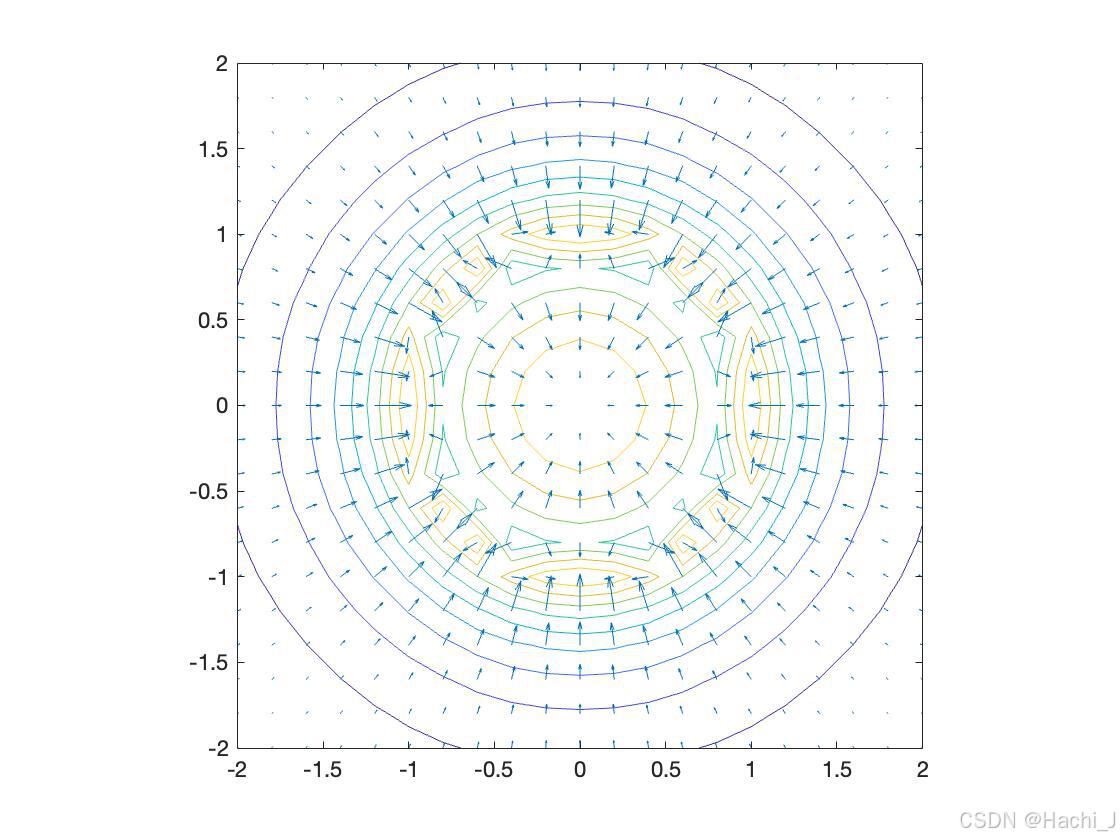

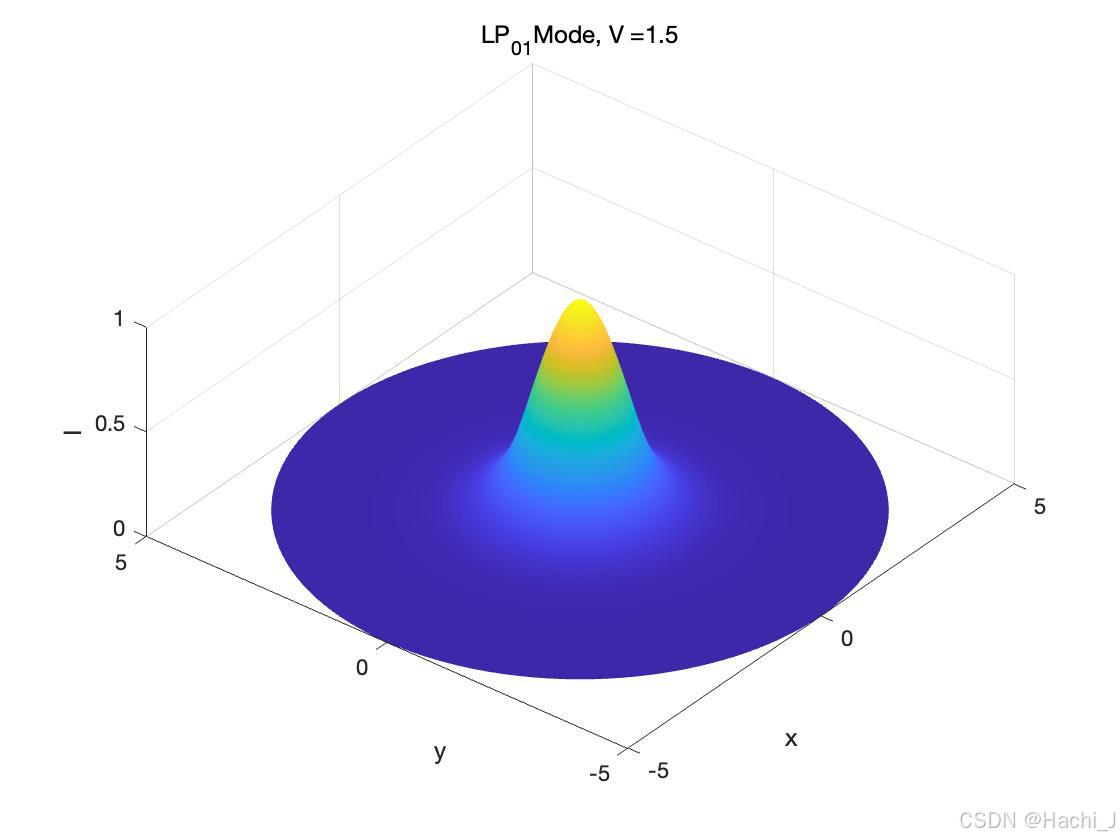
单模光纤的三维模场分布

        三维分布同理，在之前博客的参考中已经给出。

​​​​​​​