本部分的学习参考柯熙政老师的《无限光通信中的空间光——光纤耦合技术》及欧攀老师的《高等光学仿真(MATLAB版)》,为自学笔记,博客末尾附上了在学习过程中参考的博客内容。
光纤中光波的传播模式
矢量模式的解
一般采用圆柱坐标系来描述光纤中矢量模式的变化。在这里用到贝塞尔方程是因为贝塞尔方程通常在圆柱坐标系下求解,并且在光纤通信中,贝塞尔函数常用于描述光场在光纤中的分布和传播特性。
为
阶的贝塞尔函数,
为
阶的虚宗量贝塞尔函数,
为
阶的纽曼函数,
为
阶的汉克尔函数。
和
在之前的博客中提及过,
是波导的径向归一化相位常数,
是波导的径向归一化衰减常数,
是传播常数,
是波数。它们满足:
纤芯与包层的电介质常数分别为和
,考虑光纤无磁性时
,带入光纤的边界条件
时,得到特征方程:
该特征方程也称色散方程,描述光纤中波导模式的传播常数和光频率的关系。
从波动方程出发,为横向归一化常数,
为电场常数,
为磁场常数,
为光纤纤芯半径,
为圆周模式阶数(即上式的
),
是横向归一化常数为
的贝塞尔方程,
是横向归一化常数为U时的修正贝塞尔方程。
对于求解出的齐次方程,若和
有非零解,可导出光纤矢量模式的特征方程,即
利用色散方程可以确定阶模式的
值或U值。
光纤中四种矢量模式
光纤中存在四种矢量模式,分别是径向矢量光束(指偏振方向在光束横截面上沿着径向的偏振光)、角向矢量光束(指偏振方向在光束横截面上垂直于径向的偏振光)
、混合矢量偏振光束(指偏振方向在光束横截面上既包含径向分量又包含角向分量的光束)
和混合矢量偏振光束
,其中
表示圆周模式阶数,
代表径向模式阶数。
其中“TE”代表横电模(Transverse Electric Mode)指的是电场方向与传播方向垂直;“TM”代表横磁模(Transverse Magnetic Mode)指的是磁场方向与传播方向垂直;“EH”和“HE”在代表不同的混合模式;TEM 叫作横电磁模,指的是电场、磁场方向都和传播方向垂直。
在式(2-2)中,当,
时,为
模式;当
,
时,为
模式;当
取正值,为
模式;当
取负值,为
模式。相位因子
中,取“+”时,z增大、theta减小,顺时针旋转表示右旋偏振;取“-”时,z增大、theta增大,逆时针旋转表示左旋偏振。
光纤中的模式同一种光强分布对应的矢量模式有可能是不同的,如下图所示。

标量模式的解
光纤中标量模式的解为同一阶数矢量模式的简并,称线偏模,即 LPmn模式。 在弱导近似的情况下,线偏模(LP模)是由几个传播常数接近的矢量模式简并到一起形成的。

在之前的博客中我们曾经提到:
对于弱波导光纤,已经假定了其横向场的极化方向保持不变,因此可以认为它的横向场是线极化波,用LP(Linearly Polarized Mode)表示,就是人们常说的LP模(线性偏振模)。在特定条件下的传播模式,称为标量模,或模。下标m和n的值用以表明各模式的场型特性。一般来说,模式的下标m表示该模式的场分量沿光纤圆周方向的最大值有几对(沿角向的亮斑数为2m,若m为0则为中心亮斑),下标n表示该模式的场分量沿光纤半径方向的最大值有几对(沿径向的亮斑数为n)。
上一部分中提到的和
就是之前提到的m和n,LP模即是上部分提到的模的模式组合。
比如,在光纤通信中,LP11模式对应了四个简并的矢量模式,即TE01模式(角向偏振光)、TM01模式(径向偏振光)以及HE21模式的奇模和偶模。而混合矢量偏振光束可以看作是径向矢量光束和角向矢量光束的线性叠加。
光纤中的场分布采用标量近似,得到的线偏模LP模式沿z轴向的光场为
![]()
电场可以表达成以下形式:

考虑边界电场在光纤纤芯与包层分界处的连续性,左右取等号可得色散方程。我们可以对上式利用欧拉公式进行分解,可以看出电磁场沿圆周的分布由两个线偏振组成,可以得到解的形式

以上两组式子表述的波形都是光纤中的LPmn模式。随着时间的变化其偏振方向不变,这种近似的理论常称为线偏模理论。
matlab实现
贝塞尔函数
在MATLAB中提供了5中类型的贝塞尔函数,具体如下表所示:

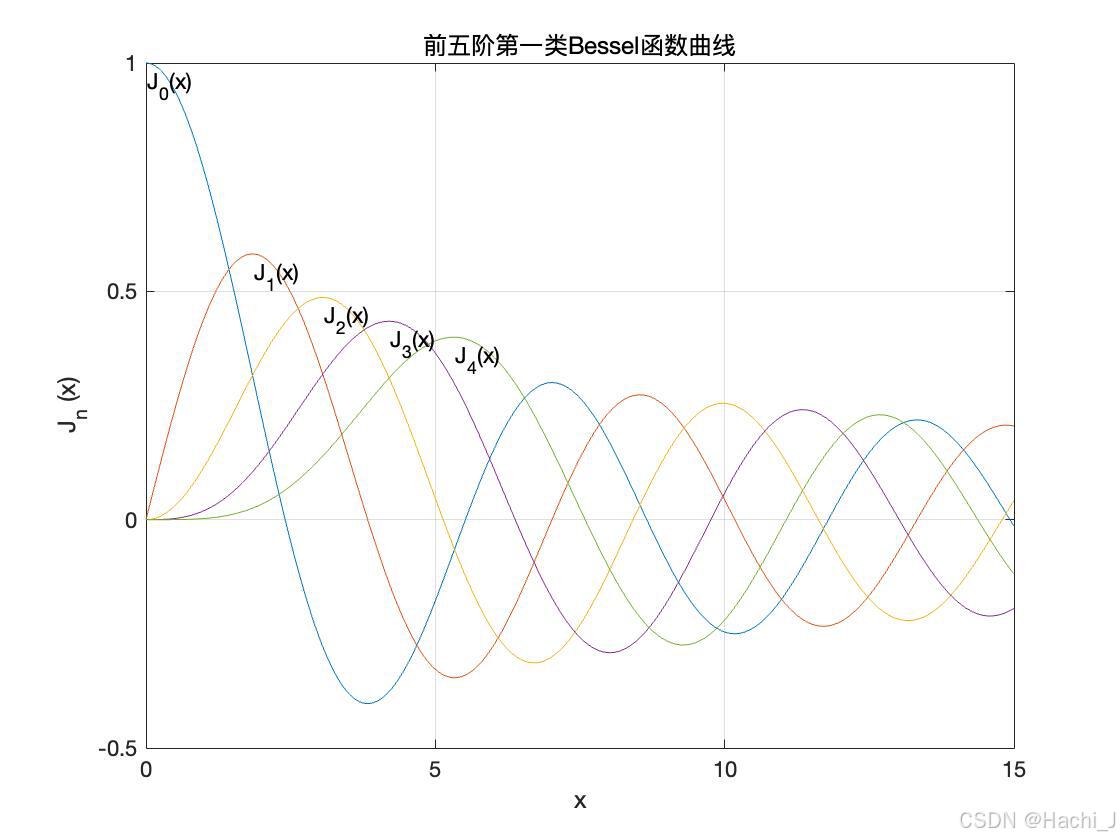
调用贝塞尔函数生成的函数曲线如下图所示:
clc;
clear;
close all;
M = 5; % 设置要作图前M阶Bessel函数
N = 1001; % 每个Bessel函数曲线的点数
Xmin = 0; % 曲线起始点
Xmax = 15; % 曲线终止点
x = linspace(Xmin,Xmax,N); % 生成起点和终点之间共N点的横坐标向量
y = zeros(N, M); % 对Bessel函数曲线数据数组y进行初始化
for m = 0:M-1
y(:,m+1) = besselj(m,x); % 将第m阶Besse1函数赋值给y的第(m+1)列
end
plot (x,y); % 画出前M阶Besse1函数曲线
[ymax pos] = max (y) ;
for i = 1:M % 标注各条曲线对应的相应阶数Besse1函数
text (x(pos(i)+1), ymax(i)-0.05, ['J_' num2str(i-1) '(x)' ]) ;
end
grid on % 加栅格
xlabel('x')
ylabel('J_n (x)')
title('前五阶第一类Bessel函数曲线') 在部分参考资料中,在包层区,当r趋向无穷时,电场应趋于零。所以选取第二类变型Bessel函数,其曲线如下图所示,可以看出该函数在r较大时呈指数规律衰减,符合物理要求。r趋于零时函数虽趋于无穷大;但包层区是限制在r>a范围内,故不会产生矛盾。
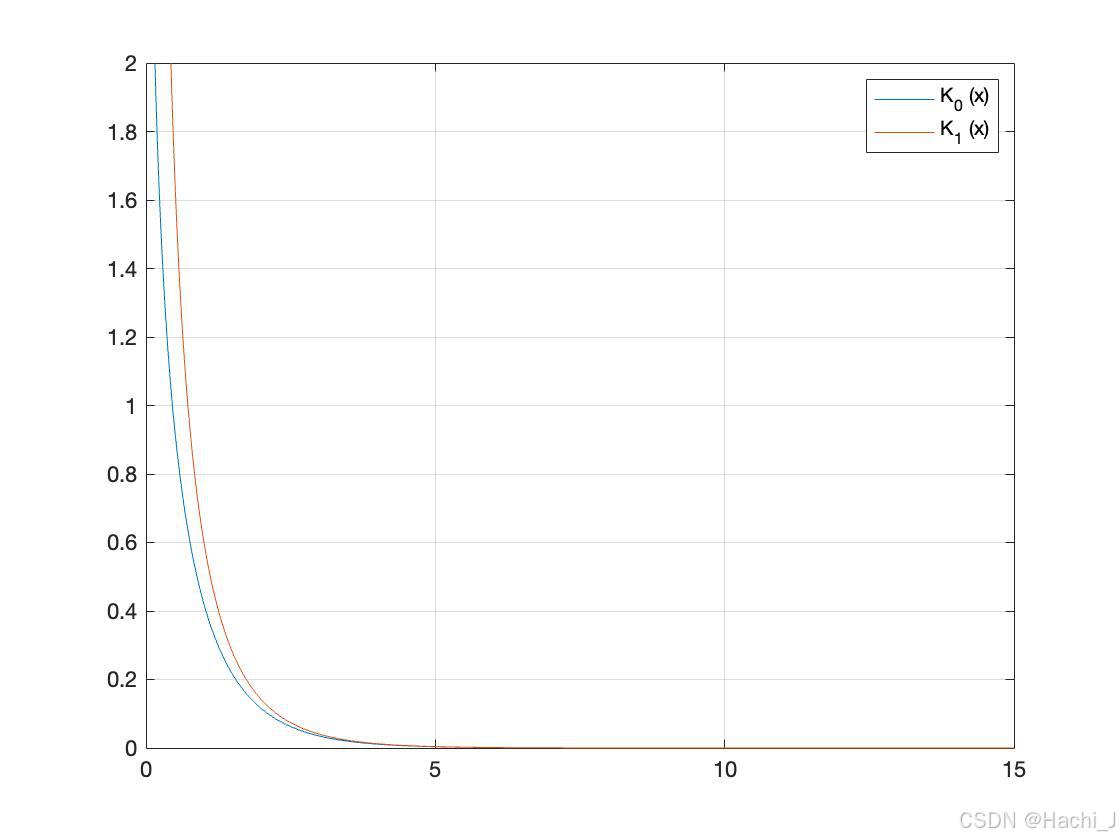
在MATLAB中对于的作图与
类似,需要调用第二类变型Bessel函数besselk(),并需要对程序进行一些修改,程序代码如下:
clc;
clear;
close all;
M=2; % 设置要作图前M阶第二类变型Besse1函数
N = 1001;
Xmin = 0;
Xmax = 15;
x = linspace (Xmin, Xmax, N) ;
y = zeros (N, M) ;
for m = 0 :M-1
y (:, m+1) = besselk (m, x) ;
end
plot (x,y) ;
legend ('K_0 (x)','K_1 (x)')
grid on
axis ([Xmin Xmax 0 2]);LP模仿真
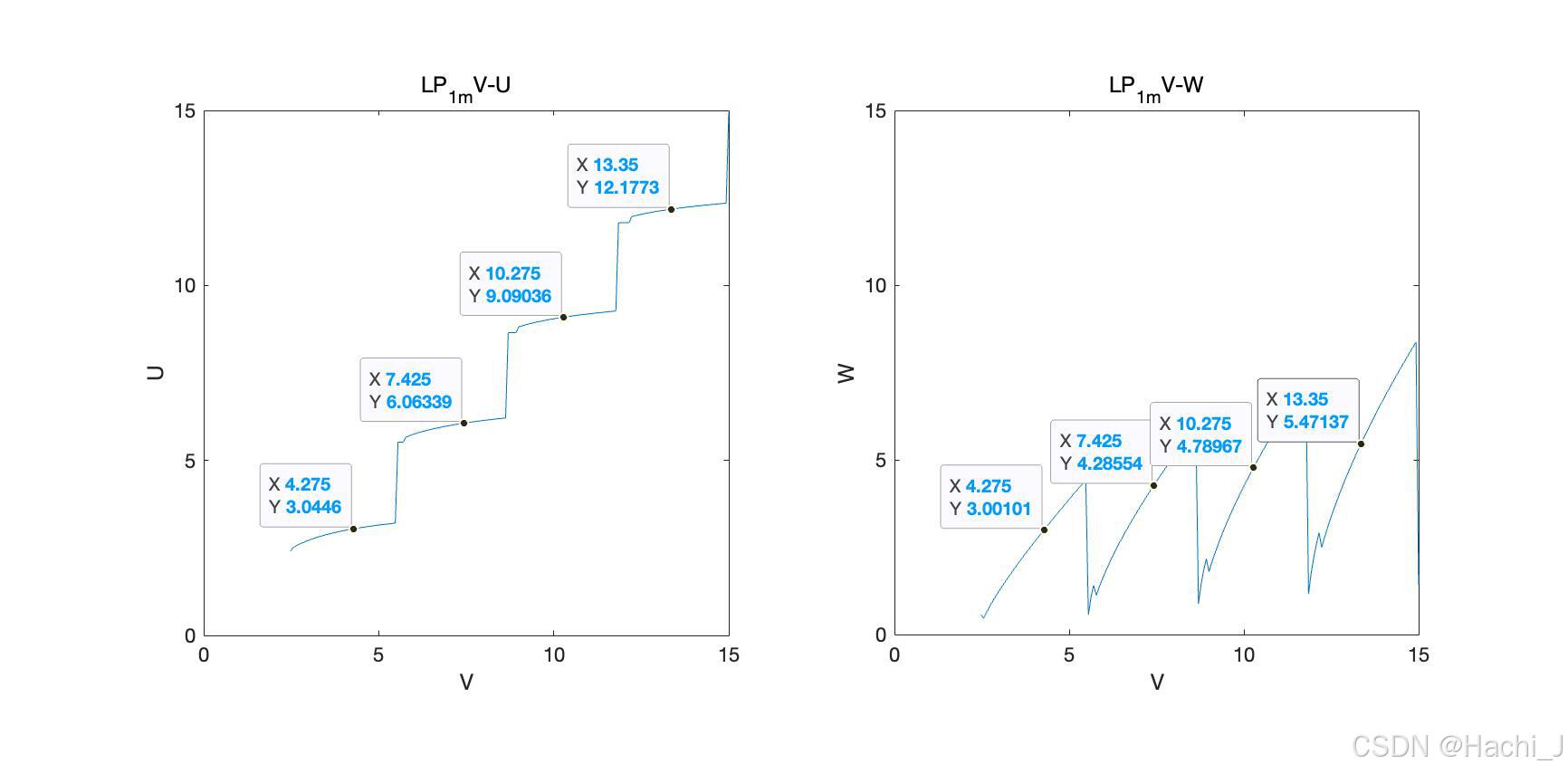
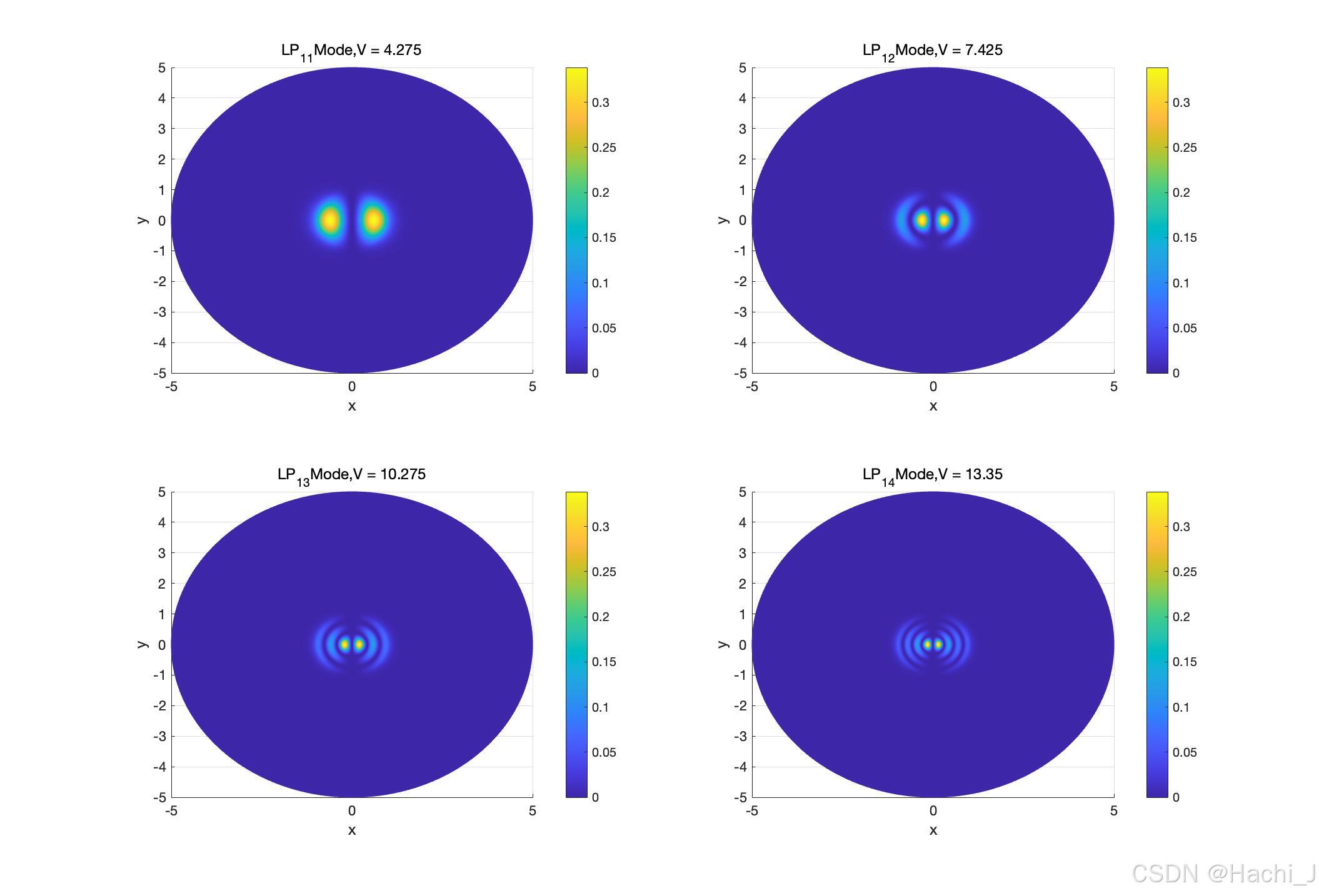
由于上文中的表格给出了不同LP模的特征方程,首先需根据对应的特征方程进行求解。U和W满足的关系在之前的博客中提过,U^2+W^2=V^2。求出特征方程的解之后,我们采用标量模式的解进行图像的绘制,带入光纤中的场分布,即可得到光纤中的仿真图样。
























 3566
3566

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








