线性规划定义和练习题集

目录

1.定义

2.matlab编程实现

3.线性规划练习题

练习题1

练习题2

 解题策略

练习题3

练习题4

练习题5 

4.总结

---

 

1.定义

在生产实际中,会遇到利润和收益最大化问题，往往会碰到统筹学的规划，线性规划可以解决一些比较简单的规划问题。

2.matlab编程实现

在matlab线性规划编程中，实现线性规划用相应的函数lingprog,不过这个函数解决的是求出最小值，在遇到最大值时，可以进行相应的转化。

3.线性规划练习题

练习题1

例1.1 某机床厂生产甲、乙两种机床，每台销售后的利润分别为4千元与3千元。生产甲机床需用A、B机器加工，加工时间分别为每台2小时和1小时;生产乙机床需用A、B、C三种机器加工，加工时间为每台各一小时。若每天可用于加工的机器时数分别为A机器10小时、B机器8小时和C机器7小时，问该厂应生产甲、乙机床各几台，才能使总利润最大?

可以分别设生产甲为x1台，生产乙为x2台，那么:

从上式可以看出决策方程为z=4x1+3x2.

matlab编程实现

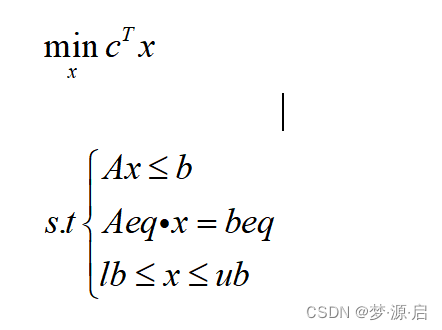
在matlab中约束分为等式约束和不等式约束。

f=[-4,-3];
a=[2,1;1,1;0,1;-1,-1];
b=[10;8;7;0];
[x,y]=linprog(f,a,b);
x,y=-y

练习题2

 求解下面线性规划问题

f=[-2;-3;5];
%如果让求最大值,填上-号
a=[-2,5,-1;1,3,1];
b=[-10;12];
aeq=[1,1,1];
beq=7;
%f为决策方程的系数,写成列向量
%a为所有不等式左边的系数,如果某一项不存在,系数写成0
%b为不等式约束右边的值
%在ligprog函数中只有<=,如果不等式约束为>=,两边同时乘上-1

%aeq为等式约束左边的系数
%beq为等式约束右边的系数
[x,y]=linprog(f,a,b,aeq,beq,zeros(3,1));
%zeros(3,1)表示是x1,x2,x3的下界,因为下界为0,所以是3个下界为0的列向量
%没有上界不用写
x,y=-y

 解题策略

在遇到不规则式子时,应当化成规则型的,然后用matlab进行求解。

例如,求min |x1|+|x2|+...+|xn|

s.t Ax<=b

其中x=[x1....xn]T.

先把上面的问题转化为线性问题，因为对于任意的xi,存在ui>0和vi>0满足

xi=ui-vi,|xi|=ui+vi.

取ui=(xi+|xi|)/2,vi=(|xi|-xi)/2就可以满足上面的条件。

这样记u=[u1,...,un]T,v=[v1,...vn]T

变成

练习题3

市场上有n种资产s;(i= 1,2,L ,n)可以选择，现用数额为M的相当大的资金作一个时期的投资。这n种资产在这一时期内购买s;的平均收益率为r，风险损失率为q4;，投资越分散，总的风险越少，总体风险可用投资的s,中最大的一个风险来度量。
购买s,时要付交易费，费率为p;，当购买额不超过给定值u;时，交易费按购买u,计算。另外，假定同期银行存款利率是r%，既无交易费又无风险（r= 5%)。
已知n=4时相关数据如表1.1。

si	ri(%)	qi(%)	pi(%)	u(元)
ui	28	2.5	1	103
s2	21	1.5	2	198
s3	23	5.5	4.5	52
s4	25	2.6	6.5	40

试给该公司设计一种投资组合方案，即用给定资金M，有选择地购买若干种资产或存银行生息，使净收益尽可能大,使总体风险尽可能小。

符号规定
s,表示第i种投资项目，如股票，债券等，i= 0,1,L ,n，其中s,指存入银行;
r,P;,4;分别表示s,的平均收益率，交易费率，风险损失率,i= 0,L ,n，其中po= 0，4%= 0;
u;表示s,的交易定额，i=1,L ,n;
x,表示投资项目s;的资金，i= 0,1,L ,n ;a表示投资风险度;
Q表示总体收益;

基本假设
(1)投资数额M相当大，为了便于计算，假设M=1;

(2)投资越分散，总的风险越小;

(3）总体风险用投资项目s,中最大的一个风险来度量;

(4) n+1种资产s;之间是相互独立的;

(5）在投资的这一时期内，rp;4;为定值，不受意外因素影响;

(6）净收益和总体风险只受r;,p;,q;影响，不受其它因素干扰。

练习题4

求解线性规划问题

                ​​​​​​​        ​​​​​​​        ​​​​​​​        ​​​​​​​        

f=[2;3;1];
a=[-1,-4,-2;-3,-2,0];
b=[-8;-6];
[x,y]=linprog(f,a,b,[],[],zeros(3,1),[]);%没有等式约束,需要空出来两个[]
%如果没有下界,需要空出一个[],如果没有上界,可以空出[],也可以省略
x,y

练习题5 

        ​​​​​​​        ​​​​​​​        ​​​​​​​        ​​​​​​​        ​​​​​​​        

f=[+5;-4;-6];
a=[1,-1,1;3,2,4;3,2,0];
b=[20;42;30];
[x,fval,exitflag,output,lambda]=linprog(f,a,b,[],[],zeros(3,1),[])
%x为x1,x2,x3的取值
%fval是最终结果
%exitflag是收敛值
%output中包含迭代次数和使用规则

4.总结

 在matlab求解线性规划方程时，默认的时求解最小值,如果让求最大值,应当先添加负号,然后最终再把求得的结果加上负号,如果某一项约束条件不存在时,应当写成[],如果末尾的上界不存在时，可以忽略不写，其余应当写成[].

牢记标准形式:

linprog=['目标函数的系数写成列向量','不等式约束系数','不等式约束值','等式约束系数','等式约束值','下界','上界']

接下来将会介绍非线性规划的求法。