机器学习之Logistic回归_logstics回归属于机器学习吗-CSDN博客

本文链接：https://blog.csdn.net/m0_72946768/article/details/139183277

一、Logistic回归概述

1.概念

Logistic回归也称作逻辑回归，是一种广泛应用于分类问题的统计学习方法，它通过将线性回归模型的输出转换为概率值来实现分类任务。在Logistic回归中，将输入特征与它们的权重相乘，然后将结果通过一个逻辑函数，即Sigmoid函数，将其转换为0到1之间的概率值。Logistic回归常用于二分类问题，例如预测一个学生是否能通过考试或者一封电子邮件是否为垃圾邮件。它也可以通过一些技巧进行扩展，用于多分类问题。Logistic回归是一种简单而有效的分类方法，广泛应用于机器学习和统计学中。

2.基本原理

Logistic回归的原理是利用线性方程和sigmoid函数来建立一个分类模型，用来预测二分类问题。Logistic回归基于线性回归，但在输出上使用了逻辑函数（如sigmoid函数）将连续的结果映射到0和1之间。具体来说，逻辑回归使用线性方程来表示输入变量和输出变量之间的关系，然后将线性方程的输出通过Sigmoid函数进行转换，将结果视为概率值。Sigmoid函数的公式为：

$eq?y%3D%5Cfrac%7B1%7D%7B1+e%5E%7B-z%7D%7D$ 。

其中，z是线性方程的输出。如果y大于0.5，则将结果预测为1，否则预测为0。

在训练逻辑回归模型时，通常使用极大似然估计来最大化模型的似然函数，以优化模型的参数（权重和偏置）。通过这种方式，模型可以学习到输入变量和输出变量之间的关系，从而进行预测。

3.优缺点

优点：

（1）简单快速：Logistic回归是一个简单且高效的分类算法，易于理解和实现。

（2）可解释性强：Logistic回归给出了不同特征对预测结果的影响程度，便于解释数据中的模式。

（3）可以处理非线性关系：通过引入特征的高次项或交互项，Logistic回归可以处理一定程度上的非线性分类问题。

缺点：

（1）容易欠拟合：Logistic回归是一种线性分类算法，对于复杂的非线性分类问题表现不佳。

（2）对异常值敏感：因为Logistic回归使用最大似然估计方法进行参数估计，对异常值敏感，容易受到噪声干扰。

（3）需要大量特征工程：Logistic回归在处理高维数据时需要进行特征选择和特征工程，否则容易出现维度灾难。

二、Logistic回归

1.线性回归

线性回归是一种用于预测数值型目标变量的统计学方法。它试图找到一条最佳直线（或者说是一个线性模型），能够最准确地描述自变量（特征）与因变量（目标变量）之间的关系。

给定由d个属性描述的示例x=(x1;x2;...xd)，其中xi是x在第i个属性上的取值，线性模型试图学习一个通过属性的线性组合来预测的函数，即 $f(x)=w_{1}x_{1}+w_{2}x_{2}+...+w_{d}x_{d}+b$ ,一般用向量形式写成 $f(x)=w^{T}x+b$ ,其中w=(w1;w2;...;wd),w和b学得之后，模型就得以确定。线性模型形式简单、易于建模，但却蕴涵着机器学习中一些重要的基本思想。许多功能更为强大的非线性模型可在线性模型的基础上通过引入层级结构或高维映射而得。此外，由于w直观表达了各属性在预测中的重要性，因此线性模型有很好的可解释性。

确定w和b的关键，在于如何衡量f(x)与之间的差别。我们可以试图让均方误差最小化，即 $(w,b)=argmin_{(w,b)}\sum_{i=1}^{m}(f(x_{i})-y_{i})^{2}=argmin_{(w,b)}\sum_{i=1}^{m}(y_{i}-wx_{i}-b)^{2}$

均方误差有非常好的几何意义，它对应于常用的欧几里得距离或简称“欧氏距离”。基于均方误差最小化来进行模型求解的方法称为“最小二乘法”。在线性回归中，最小二乘法就是试图找到一条直线，使所有样本到直线上的欧氏距离之和最小。

2.Sigmoid函数

在logistic回归中，Sigmoid函数是一种常用的激活函数，用于将线性模型的输出转换为0到1之间的概率值。Sigmoid函数的公式为：

$eq?f%28z%29%3D%5Cfrac%7B1%7D%7B1+e%5E%7B-z%7D%7D$

其中，z为输入的线性组合，即 $eq?z%3Dw_%7B0%7Dx_%7B0%7D+w_%7B1%7Dx_%7B1%7D+...+w_%7Bn%7Dx_%7Bn%7D$ ,其中w0,...,wn为模型参数，x0,...xn为输入特征。

Sigmoid函数的图像呈S形曲线，图像如下。Sigmoid函数具有以下特点：在z接近负无穷时，f(z)接近0；在z接近0时，f(z)等于0.5；在z接近正无穷时，f(z)接近1。

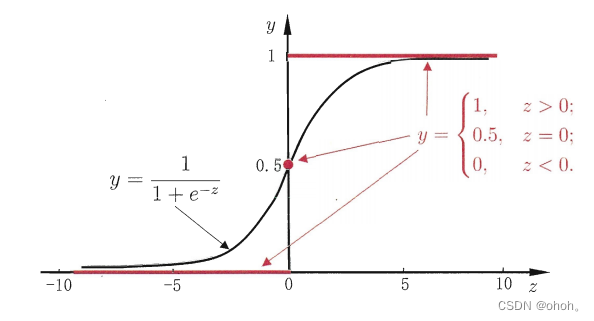
Sigmoid函数将线性模型的输出映射到一个概率范围内，可以用来表示二分类问题中某个类别的概率。在logistic回归中，我们通常将Sigmoid函数应用于线性模型的输出以预测目标变量的概率。通过设置合适的阈值，可以将概率转换为分类结果。

3.极大似然估计

在Logistic回归中，我们通常使用极大似然估计来估计模型参数。在极大似然估计中，假设观测数据是独立同分布的，并且服从伯努利分布（即二分类问题）。我们的目标是通过观测数据来估计模型参数，使得观测数据出现的概率最大化。

对于Logistic回归模型来说，我们通常假设观测数据服从二项分布，其中因变量的概率分布由Logistic函数所控制。Logistic函数的形式为： $eq?P%28y%3D1%7Cx%29%3D%5Cfrac%7B1%7D%7B1+e%5E%7B-%5Cbeta%20T_%7Bx%7D%7D%7D$ .

其中，y为因变量的取值（0或1），x为自变量的取值，β为模型参数。

我们的似然函数可以表示为： $eq?L%28%5Cbeta%20%29%3D%5Cprod_%7Bn%7D%5E%7Bi%3D1%7DP%28y_%7Bi%7D%7Cx_%7Bi%7D%3B%5Cbeta%20%29$ .

最终的极大似然估计是通过最大化似然函数得到的： $eq?%5Chat%7B%5Cbeta%20%7D%3Dargmax_%7B%5Cbeta%20%7DL%28%5Cbeta%20%29$ .

一般来说，我们使用梯度下降等优化算法来求解上述最优化问题。最终得到的参数 $eq?%5Chat%7B%5Cbeta%20%7D$ 即为Logistic回归模型的参数估计值。通过极大似然估计，我们可以得到最优的Logistic回归模型参数，进而用于对未知数据进行分类预测。需要注意的是，在实际问题中，由于可能存在过拟合等问题，还需要对模型进行正则化等处理来提高模型的泛化能力。

4.梯度上升法

梯度上升法是一种优化算法，用于找到函数的最大值。在Logistic回归中，我们需要最大化似然函数来找到最佳的模型参数，这就需要使用梯度上升法来迭代地更新参数值。

具体来说，梯度上升法的步骤如下：
（1）初始化模型参数，一般可以随机初始化。
（2）计算误差，根据当前模型参数计算出预测值与实际值之间的误差。
（3）计算梯度，根据误差计算出当前模型参数的梯度。
（4）更新参数，按照梯度的方向更新参数值。
（5）重复步骤（2）-（4），直到达到收敛条件。

在每次更新参数的时候，需要乘以一个学习率来调节步长，避免在更新过程中发散或者收敛太慢。梯度上升法可以帮助我们找到Logistic回归的最优参数，从而得到一个最佳的分类模型。需要注意的是，梯度上升法是一种局部搜索算法，可能会陷入局部最优解。因此可以多次随机初始化参数，然后取最优的参数作为最终结果，或者使用其他优化算法，如随机梯度下降等。

三、Logistic回归具体实现

以身高、体重作为特征，分析这两种因素对于是否肥胖的分类结果的影响，记肥胖为“0”，非肥胖为“1”，具体实现过程如下：

1.过程分析

（1）加载数据

def load_data():
    data = np.array([[155, 70, 0],[156,73,0],[153,40,1],[176,78,1],[188,70,1],[167,58,1],[180,130,0],[160,76,0],[175,85,0],[172,85,0],[177,80,1],[166,75,0],[161,69,0],[180,80,1],[167,54,1],
                     [170, 75, 1],[195,100,1],[163,54,1],[167,55,1],[179,68,1],[159,67,0],[172,77,0],[184,78,1],[176,120,0],[178,80,1],[148,34,1],[170,57,1],[165,78,0],[159,45,1],[174,65,1],
                     [165, 68, 0],[190,94,1],[175,59,1],[156,70,0],[150,45,1],[187,88,1],[167,57,1],[147,59,0],[178,90,0],[159,52,1],[163,58,1],[174,64,1],[176,83,0],[187,85,1],[172,80,0]])
    X = data[:, :2]
    y = data[:, 2]
    return X, y

（2）定义sigmoid函数

def sigmoid(z):
    return 1 / (1 + np.exp(-z))

（3）使用梯度上升法训练模型

def train(X, y, alpha=0.01, max_iters=1000):
    m, n = X.shape
    X = np.hstack((np.ones((m, 1)), X))
    weights = np.zeros(n + 1)

    for _ in range(max_iters):
        y_pred = sigmoid(np.dot(X, weights))
        error = y - y_pred
        gradient = np.dot(X.T, error)
        weights += alpha * gradient

    return weights

（4）迭代算法，输出不同迭代次数的预测准确率

iterations = [10,30,50,100,300,500,700,1000,2000,5000]
for n_iter in iterations:
    weights = train(X, y, max_iters=n_iter)
    y_pred = predict(X, weights)
    acc = accuracy(y, y_pred)
    print("迭代次数为{}时的预测准确率：{}".format(n_iter, acc))

2.具体代码实现

import numpy as np
import matplotlib.pyplot as plt
# 加载数据
def load_data():
    data = np.array([[155, 70, 0],[156,73,0],[153,40,1],[176,78,1],[188,70,1],[167,58,1],[180,130,0],[160,76,0],[175,85,0],[172,85,0],[177,80,1],[166,75,0],[161,69,0],[180,80,1],[167,54,1],
                     [170, 75, 1],[195,100,1],[163,54,1],[167,55,1],[179,68,1],[159,67,0],[172,77,0],[184,78,1],[176,120,0],[178,80,1],[148,34,1],[170,57,1],[165,78,0],[159,45,1],[174,65,1],
                     [165, 68, 0],[190,94,1],[175,59,1],[156,70,0],[150,45,1],[187,88,1],[167,57,1],[147,59,0],[178,90,0],[159,52,1],[163,58,1],[174,64,1],[176,83,0],[187,85,1],[172,80,0]])
    X = data[:, :2]
    y = data[:, 2]
    return X, y
# 定义 sigmoid 函数
def sigmoid(z):
    return 1 / (1 + np.exp(-z))
# 使用梯度上升法训练模型
def train(X, y, alpha=0.01, max_iters=1000):
    m, n = X.shape
    X = np.hstack((np.ones((m, 1)), X))
    weights = np.zeros(n + 1)

    for _ in range(max_iters):
        y_pred = sigmoid(np.dot(X, weights))
        error = y - y_pred
        gradient = np.dot(X.T, error)
        weights += alpha * gradient

    return weights

# 预测函数
def predict(X, weights):
    m = X.shape[0]
    X = np.hstack((np.ones((m, 1)), X))
    y_pred = sigmoid(np.dot(X, weights))
    return y_pred

# 计算准确率
def accuracy(y_true, y_pred):
    y_pred_class = (y_pred >= 0.5).astype(int)
    acc = np.mean(y_pred_class == y_true)
    return acc

# 加载数据
X, y = load_data()

# 使用梯度上升法训练模型
weights = train(X, y)

# 画出分类的散点图
plt.scatter(X[y == 0][:, 0], X[y == 0][:, 1], color='blue', label='非肥胖')
plt.scatter(X[y == 1][:, 0], X[y == 1][:, 1], color='red', label='肥胖')

# 预测输出分类结果
X_test = np.array([[168, 65]])
pred = predict(X_test, weights)
print("预测分类结果：", '肥胖' if pred >= 0.5 else '非肥胖')

# 输出预测结果的准确率
y_pred = predict(X, weights)
acc = accuracy(y, y_pred)
print("预测准确率：", acc)

# 迭代算法，输出不同迭代次数的预测准确率
iterations = [10,30,50,100,300,500,700,1000,2000,5000]
for n_iter in iterations:
    weights = train(X, y, max_iters=n_iter)
    y_pred = predict(X, weights)
    acc = accuracy(y, y_pred)
    print("迭代次数为{}时的预测准确率：{}".format(n_iter, acc))

plt.legend()
plt.xlabel('身高(cm)')
plt.ylabel('体重(kg)')
plt.show()

3.运行结果情况及结果分析

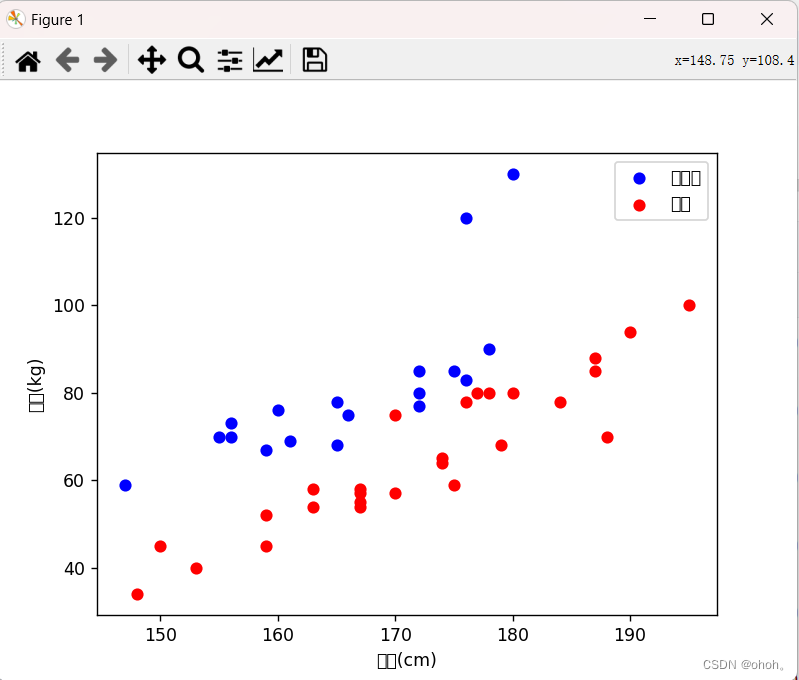
（1）训练集的散点图分布如下：

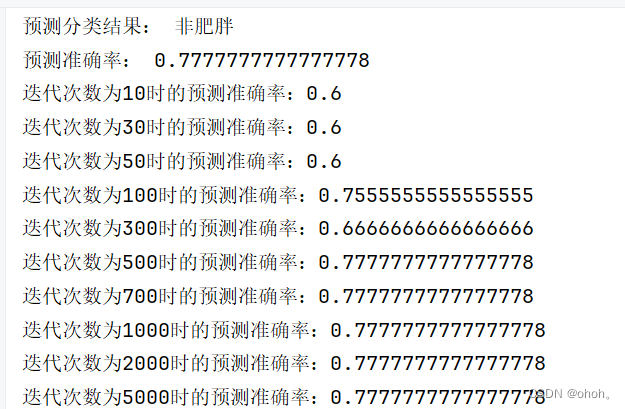
（2）根据给定的测试集进行分类，得到分类结果及预测准确率，多次迭代后得到预测准确率如下：

（3）结果分析

根据代码的运行结果，预测结果为"非肥胖"，预测准确率为0.7777777777777778。根据迭代次数的不同，可以看到随着迭代次数的增加，预测准确率也在逐步提高。这表明模型在训练集上表现良好，能够准确地区分出肥胖和非肥胖人群。通过散点图可以观察到，数据点大致呈现出两个类别的聚集情况，分类边界可能是一条直线，模型通过训练找到了这个边界，达到了很高的准确率。整体来看，模型在这个数据集上表现良好，能够有效地分类肥胖和非肥胖人群。

四、实验总结

Logistic回归是一种常用的分类模型，主要用于处理二分类问题，它通过将线性回归的结果通过sigmoid函数进行转换，将特征的线性组合映射到[0,1]的区间，从而得到样本属于某个类别的概率预测值。在Logistic回归中，我们可以采用极大似然估计的方法来估计模型参数，即最大化给定数据集下的似然函数，求得最优参数使得观测到的数据出现的概率最大。我们可以通过梯度上升法来求解最大似然估计的参数，通过不断迭代更新参数，使得损失函数逐渐收敛到最小值。通过观察训练集和测试集的损失函数值和分类准确率，可以评估模型的性能和泛化能力。

总的来说，Logistic回归是一种简单而有效的分类算法，通过线性回归与sigmoid函数的结合，极大似然估计和梯度上升法的优化，可以实现对样本的二分类问题的预测。通过实验验证和参数调优，我们可以得到一个效果较好的模型。