0-1背包

算法原理

基本思路是构建一个二维数组 dp[i][j] ，其中 dp[i][j] 表示在前 i 个物品中，背包容量为 j 时的最大价值。动态规划的状态转移方程如下：

1. 当第 i 个物品的重量大于背包容量 j 时，dp[i][j] = dp[i-1][j]，即当前物品无法放入背包。
2. 当第 i 个物品的重量小于等于背包容量 j 时，dp[i][j] = max(dp[i-1][j]，dp[i-1][j-w[i]] + v[i])，即选择放入第 i 个物品和不放入情况中的最大值。

最后， dp[n][W] 即为问题的最优解，其中 n 为物品数量， W 为背包容量。

测试数据

数据一

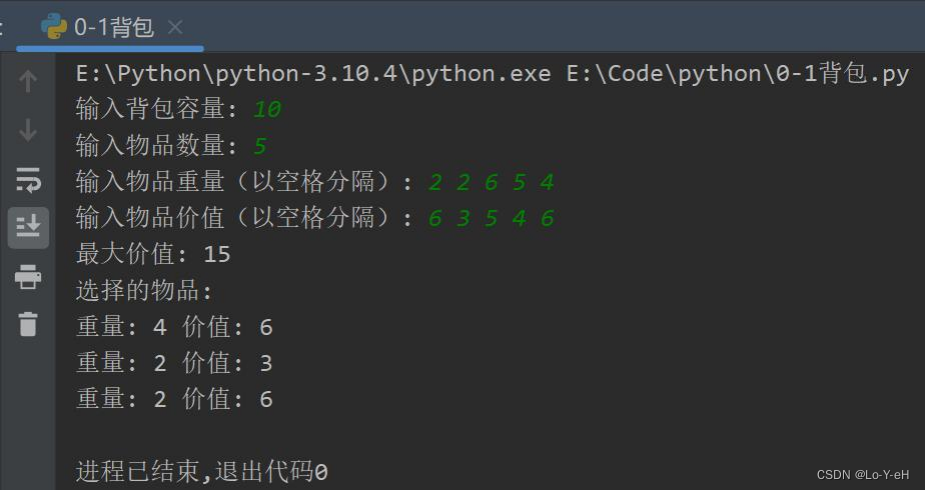
背包容量： 10

物品数量： 5

物品重量： [2, 2, 6, 5, 4]

物品价值： [6, 3, 5, 4, 6]

数据二

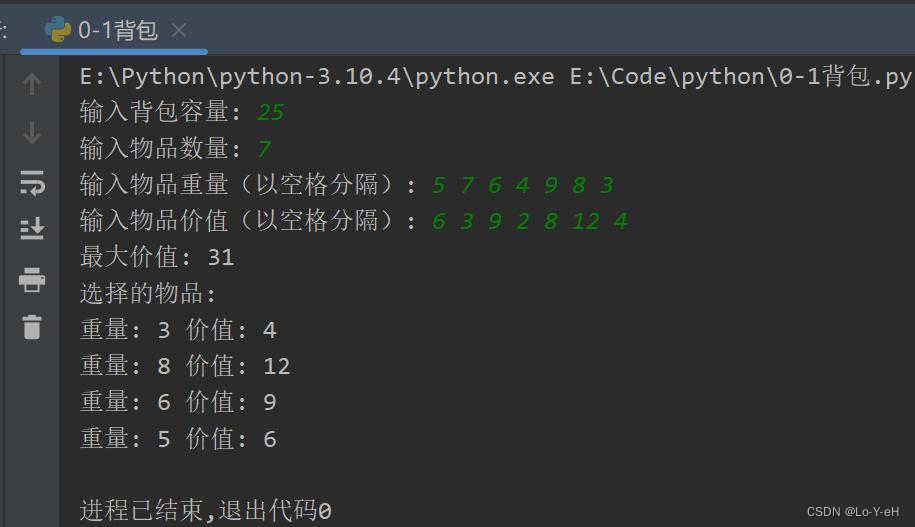
背包容量： 25

物品数量： 7

物品重量： [5, 7, 6, 4, 9, 8, 3]

物品价值： [6, 3, 9, 2, 8, 12, 4]

主要流程

1. 定义背包容量 capacity、物品数量 n、物品重量 weight 和物品价值 value
2. 初始化动态规划数组 dp，并将所有元素初始化为 0。
3. 使用双重循环遍历物品和背包容量，根据状态转移方程计算 dp 数组。
4. 根据 dp 数组的最后一个元素 dp[n][W]，得到问题的最优解。
5. 返回最优解。

主要模块功能

• 初始化：初始化动态规划数组 dp 和其他变量
• 动态规划：双重循环遍历物品和背包容量，根据状态转移方程计算 dp 数组
• 获取最优解：根据 dp 数组的最后一个元素 dp[n][W]，得到问题的最优解

数据结构设计

• 数组 dp：二维数组，存储在前 i 个物品中，背包容量为 j 时的最大价值。
• 其他变量：背包容量、物品数量、物品重量和物品价值

源代码

def knapsack(capacity, weights, values):
    n = len(weights)
    dp = [[0] * (capacity + 1) for _ in range(n + 1)]
    selected_items = [[False] * (capacity + 1) for _ in range(n + 1)]

    for i in range(1, n + 1):
        for j in range(1, capacity + 1):
            if weights[i - 1] <= j:
                if values[i - 1] + dp[i - 1][j - weights[i - 1]] > dp[i - 1][j]:
                    dp[i][j] = values[i - 1] + dp[i - 1][j - weights[i - 1]]
                    selected_items[i][j] = True
                else:
                    dp[i][j] = dp[i - 1][j]
            else:
                dp[i][j] = dp[i - 1][j]

    selected = []
    i = n
    j = capacity
    while i > 0 and j > 0:
        if selected_items[i][j]:
            selected.append((weights[i - 1], values[i - 1]))
            j -= weights[i - 1]
        i -= 1

    return dp[n][capacity], selected


capacity = int(input("输入背包容量: "))
n = int(input("输入物品数量: "))

weights_input = input("输入物品重量（以空格分隔）: ")
weights = list(map(int, weights_input.split()))
values_input = input("输入物品价值（以空格分隔）: ")
values = list(map(int, values_input.split()))

max_value, selected_items = knapsack(capacity, weights, values)
print("最大价值:", max_value)
print("选择的物品:")
for item in selected_items:
    print("重量:", item[0], "价值:", item[1])

运行结果

测试用例1

测试用例2

时间复杂度

1. 初始化部分：创建了两个二维数组 dp 和 selected_items，其大小为 (n+1)× (capacity+1)。初始化这两个数组的时间复杂度为 O(n × capacity)。
2. 动态规划部分：使用双重循环遍历物品和容量，计算每个状态的最优解。外层循环遍历物品数量 n，内层循环遍历背包容量 capacity。在每个状态下，根 据当前物品的重量和价值，更新 dp 数组和 selected_items 数组。循环体中的操作都是常数时间复杂度的。因此，该部分的时间复杂度为 O(n × capacity)。
3. 回溯部分：根据 selected_items 数组回溯选中的物品。回溯的次数最多为n，每次回溯的操作是常数时间复杂度的。因此，该部分的时间复杂度为O(n)。

综上所述，算法的总时间复杂度为 O(n × capacity) 。其中 n 为物品数量，capacity 为背包容量。

小结

动态规划是一种有效解决复杂问题的算法方法。通过将问题划分为子问题，并利用子问题的最优解来求解原问题，动态规划能够高效地找到最优解。在 0-1 背包问题中，需要选择物品放入背包，使得总价值最大化且不超过背包容量限制。动态规划算法的关键是定义状态和状态转移方程，利用二维数组存储子问题的最优解，并通过迭代计算出整个问题的最优解。