FTA故障树分析

1. 故障树的术语与符号

1.1 故障树分析的定义

故障树分析是产品安全性，可靠性的分析工具之一

1.2 事件的定义

• 事件：描述系统或零件故障的状态
• 顶事件：是故障树分析中所关心的最后结果事件。它位于故障树顶端，总是逻辑门的输出事件而不是输入事件。
• 底事件：是故障树中导致其他事件的原因事件。它位于故障树的底端。它总是逻辑门的输入事件而不是输出事件。底事件分为基本事件与未探明事件。

1.3 事件的符号

1.4 逻辑门的术语与符号

• 顺序与门：在故障树分析（FTA）中用来描述事件之间的逻辑关系。顺序与门表示输入事件既要都发生，又要按一定的顺序发生，输出事件才会发生。这种门在分析系统故障或事故原因时非常重要，因为它能帮助识别出那些不仅必须发生，而且必须按照特定顺序发生的事件。

逻辑门下面的事件是输入事件，上面是输出事件

2. 故障树的建立

下面以一个电机合电后不工作为例，讲解一下故障树的建立

• 电路的构成为电机，电源，导线，开关组成
• 顶事件为“开关合上后电机不转”

2.1 故障树分析的一般步骤

1. 准备工作：熟悉设计的说明，原理图，结果图，运行与维修的规程
2. 确认顶事件：选择最不希望发生的事件为顶事件
3. 建立故障树：使用逻辑门进行分析

2.2 确认顶事件的原则

• 选择影响陈品计数性能、经济型、可靠性和安全性的故障
• 选择FMECA中严酷度为Ⅰ，Ⅱ类的故障
• 重大故障或事故作为顶事件、故障归零的依据
• 顶事件必须严格定义

2.3 建立故障树的基本原则

• 明确边界条件，进行适当简化
  建立故障树之前，根据分析的目的，明确分析的系统与其他系统的接口边界。同时做一些必要的假设（比如不考虑人的因素，某些设备或线路的故障）。

  • 边界条件应包括：
    初始状态。当系统中的部件有数种工作状态时，应指明与顶事件发生有关部件的工作状态；
    不容许事件。建立故障树的过程中认为不容许发生的事件；
    必然事件。在一定条件下必然发生的事件和必然 不发生的事件。

• 故障事件要严格定义
  明确故障是什么，和什么情况下发生故障。

• 从上向下逐级建树

• 用直接事件逐步取代间接事件

  1. 假设在构建一个关于汽车无法启动的故障树时，最初可能将“点火系统故障”作为一个中间事件。
  2. 随着分析的进行，这个中间事件可能会被更具体的直接事件所取代，如“火花塞不点火”、“点火线圈故障”等。
  3. 最终，这些直接事件将帮助维修人员准确地定位并解决问题。
     

• 处理共因事件和互斥事件

  • 共因事件：
  • 互斥事件：不可能同时发生的事件

3. 故障树的定性分析

• 寻找导致顶事件发生原因和原因组合，识别导致顶事件发生的所有故障模式。

3.1 最小割集

• 割集
  一些事件的集合，当这些底事件同时发生时，顶事件必然发生。
  如下示例，三个集合都是割集
  

• 最小割集
  最小割集的含义：
  将割集中所含的底事件任意去掉一个就不再称为割集。最小割集代表了引起顶事件发生的故障原因。
  

• 最小割集的阶数：
  最小割集的阶数指的是构成该最小割集的基本事件（或称为底事件）的数量。

• 最小割集求法

  • 下行法：

  • 上行法：

    

3.2 最小割集的定性比较

• 阶数越小的最小割集越重要：{X1} {X2,X3} {X4,X5,X6}
• 在低阶最小割集中出现的底事件比高阶最小割集中的底事件重要 {X2,X3} {X4,X5,X6}
• 在最小割集阶数相同的条件下，在不同最小割集中重复出现的次数越多的底事件越重要{X1,X2,X3},{X1,X2,X4},{X1,X3,X5}三个同阶最小割集中，X1重复出现的次数最多，那么它就是最重要的。

4. 故障树的定量分析

• 顶事件发生的概率计算
  通过集合与概率计算，计算出顶事件发生的概率
  

  • 目的：
    确定顶事件的发生概率
    确定底事件的重要度

  • 使用容斥定理进行顶事件的概率的计算：
    $\begin{array}{rl}P(T)& =P\left(K_1\cup K_2\cup \cdots \cup K_{N_k}\right)\\ & =\sum _{i=1}^{N_k}P\left(K_i\right)-\sum _{i<j=2}^{N_k}P\left(K_i{K}_j\right)+\sum _{i<j<k=3}^{N_k}P\left(K_i{K}_j{K}_k\right)+\cdots +(-1{)}^{N_k-1}P\left(K_1,K_2,\cdots K_{N_k}\right)\end{array}$

• 底事件重要度分析的示例
  简单来说就是一个若干个底事件中，某个底事件的微小变化导致顶事件的变化最大。这个底事件就是最重要的。由此可见，需要进行偏分计算。
  如下：
  

5. 故障树的规范化与简化

5.1 故障树的规范化

• 未探明事件的2种处理方法：

  • 当作基本事件
  • 删去

• 顺序与门变换为与门
  

• 表决门变换为或门和与门的组合
  

• 异或门变换为或门，与门和非门的组合
  

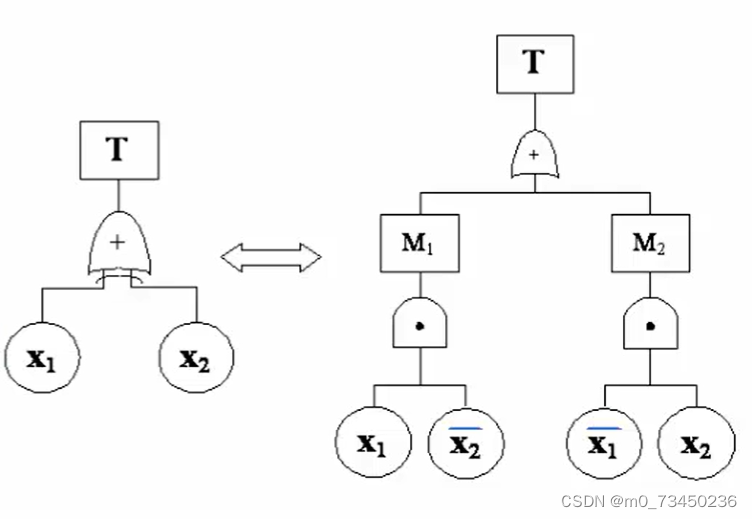
• 禁门变换为与门
  

5.2 故障树的简化

去掉明显的逻辑多余事件和明显的逻辑多余门

6. 故障树工程应用要点