故障树最小割集计算指南：从逻辑解析到Java代码实战，手把手教你定位系统失效关键路径

最近在工作中遇到了FTA（故障树分析）相关的问题，主要是因为最近的工作和可靠性分析相关。由于之前没有接触过最小割集的概念和计算方法，想要梳理一下思路帮助自己理解，也希望能帮到遇到同样问题的朋友。

想要计算故障树的最小割集，首先要明确故障树和最小割集的概念。考虑到这两个概念并不是本文的重点，能来搜索计算最小割集的朋友，至少都对故障树有一定认识，这里就不展开论述了，只列出相关概念帮大家回忆和理解。

故障树‌是以顶事件（系统故障）为根、底事件（部件故障）为叶的逻辑模型，通过“与门”“或门”描述事件因果关系。‌

最小割集‌是导致顶事件发生的最简底事件组合（任一子集失效时顶事件不成立）。计算时需解析故障树结构，剔除冗余事件，识别关键失效路径，为系统可靠性优化提供依据。

明确了概念之后，想要计算最小割集，还需要明确一些计算的规则：

关键规则
与门（AND）‌：横向扩展当前行，保留所有事件。
或门（OR）‌：纵向展开为多行，每行对应一个分支。
剔除冗余‌：若某割集是另一割集的超集（如 {A,B,C} 包含 {A,B}），则删除前者。

准备工作完成后，我们开始进入故障树的最小割集计算。

以下使用‌下行法（行列法）‌逐步计算故障树的最小割集，通过一个具体案例演示过程：

假设顶事件 ‌T‌ 由两个中间事件 ‌M1‌ 和 ‌M2‌ 通过‌与门‌连接：

M1‌ = ‌X₁‌ ∨ ‌X₂‌（或门）
M2‌ = ‌X₃‌ ∧ ‌X₄‌（与门）

故障树逻辑表达式为：

𝑇=𝑀1∧𝑀2=(𝑋1∨𝑋2)∧(𝑋3∧𝑋4)

步骤详解‌
1. 初始化：从顶事件开始‌

初始行为顶事件组合：

[𝑀1,𝑀2]

2. 分解第一层逻辑门‌
M₁ 是或门‌（∨）：纵向展开为两行，每行包含一个分支：

[𝑋1,𝑀2]和[𝑋2,𝑀2]
M₂ 是与门‌（∧）：横向扩展为单个行，保留当前组合：

[𝑋1,𝑋3,𝑋4]和[𝑋2,𝑋3,𝑋4]
3. 检查底事件组合‌

最终得到两行底事件组合：

{X₁, X₃, X₄}‌
{X₂, X₃, X₄}‌
4. 筛选最小割集‌
{X₁, X₃, X₄}‌ 和 ‌{X₂, X₃, X₄}‌ 均包含3个底事件，且无法通过删除任意一个事件仍保证顶事件发生。
因此，最小割集为上述两组‌。

复杂案例扩展‌

若故障树更复杂（例如含多层级与门、或门混合），需逐层展开并剔除冗余：

案例扩展结构‌

假设顶事件 ‌T‌ = ‌M1‌ ∧ ‌M2‌，其中：

M1‌ = (‌X₁‌ ∧ ‌X₂‌) ∨ ‌X₃‌（或门）
M2‌ = ‌X₄‌ ∨ (‌X₅‌ ∧ ‌X₆‌)（或门）

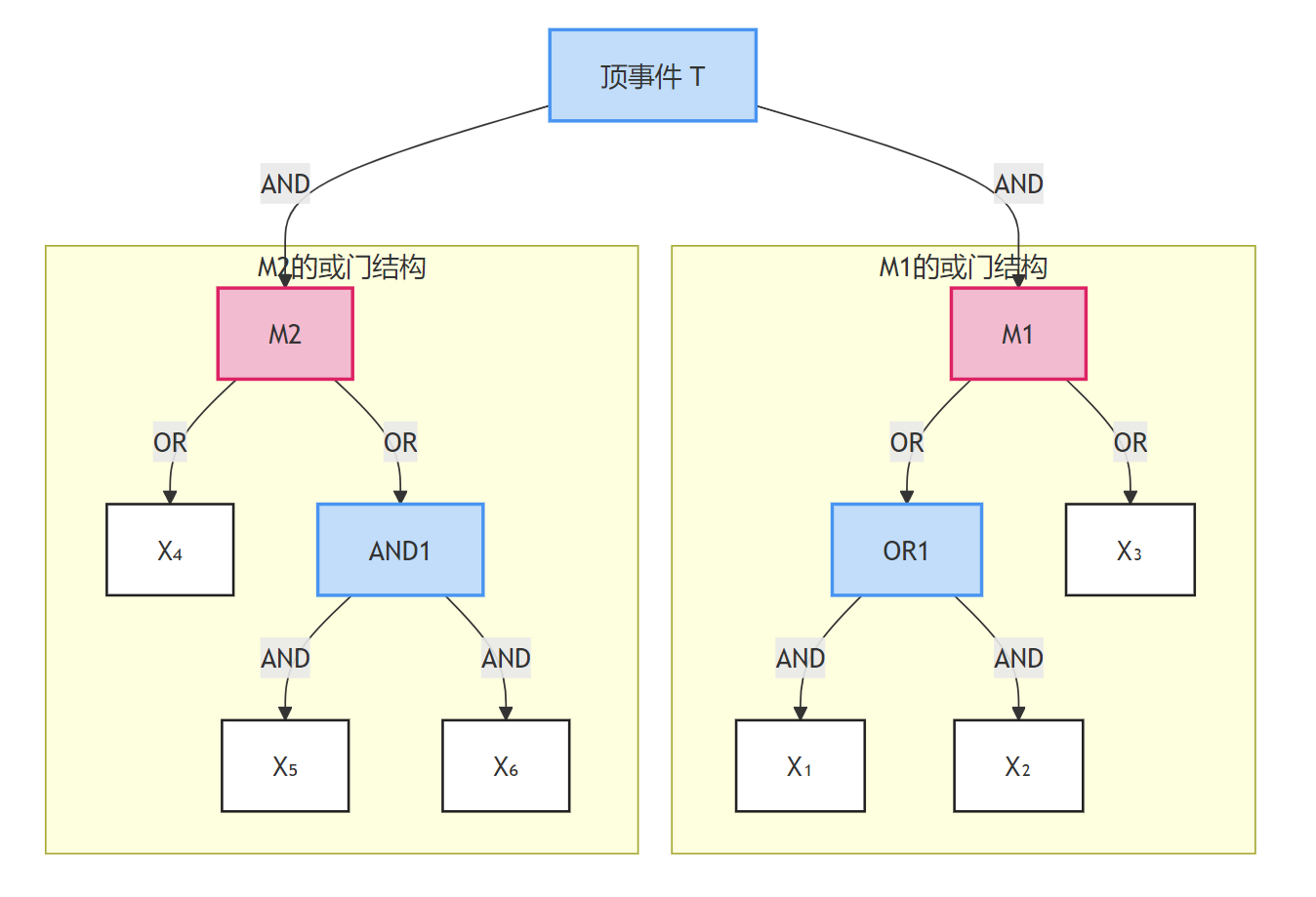
计算过程‌

初始行‌：

[𝑀1,𝑀2]

分解 M₁（或门）‌：

分支1：‌[X₁, X₂, M₂]‌（对应 ‌X₁ ∧ X₂‌）
分支2：‌[X₃, M₂]‌（对应 ‌X₃‌）

分解 M₂（或门）‌：

分支1‌：
[X₁, X₂, X₄]‌（对应 ‌X₄‌）
[X₁, X₂, X₅, X₆]‌（对应 ‌X₅ ∧ X₆‌）
分支2‌：
[X₃, X₄]‌
[X₃, X₅, X₆]‌

筛选最小割集‌：

{X₃, X₄}‌（2个事件）
{X₁, X₂, X₄}‌（3个事件）
{X₃, X₅, X₆}‌（3个事件）
{X₁, X₂, X₅, X₆}‌（4个事件）

最终最小割集‌：

{𝑋3,𝑋4},{𝑋1,𝑋2,𝑋4},{𝑋3,𝑋5,𝑋6},{𝑋1,𝑋2,𝑋5,𝑋6}‌

注意：根据剔除冗余的规则，如果结果中有子集的情况，要保留子集而去除父集。

通过逐层替换逻辑门并筛选，可系统化求得最小割集。此方法适合手动计算或编程实现，尤其适用于多层级复杂故障树。

大家如果有兴趣，可以运行以下代码，体会一下在代码中是如何计算最小割集的，希望能帮大家加深理解。

import java.util.*;

class TreeNode {
    enum Type { BASIC, AND_GATE, OR_GATE }
    Type type;
    String name;
    List<TreeNode> children = new ArrayList<>();

    public TreeNode(Type type, String name) {
        this.type = type;
        this.name = name;
    }
}

public class FaultTreeAnalysis {

    // 计算最小割集入口方法
    public static Set<Set<String>> calculateMinimalCutSets(TreeNode root) {
        Queue<List<TreeNode>> queue = new LinkedList<>();
        queue.add(Collections.singletonList(root));
        Set<Set<String>> cutSets = new HashSet<>();

        while (!queue.isEmpty()) {
            List<TreeNode> currentPath = queue.poll();
            List<List<TreeNode>> expandedPaths = expand(currentPath);

            for (List<TreeNode> path : expandedPaths) {
                if (isAllBasicEvents(path)) {
                    cutSets.add(getBasicEventSet(path));
                } else {
                    queue.add(path);
                }
            }
        }

        return removeSupersets(cutSets);
    }

    // 展开逻辑门
    private static List<List<TreeNode>> expand(List<TreeNode> path) {
        List<List<TreeNode>> result = new ArrayList<>();
        for (int i = 0; i < path.size(); i++) {
            TreeNode node = path.get(i);

            if (node.type == TreeNode.Type.AND_GATE) {
                // 与门：横向扩展子节点
                List<TreeNode> newPath = new ArrayList<>(path);
                newPath.remove(i);
                newPath.addAll(i, node.children);
                result.add(newPath);
                // 与门只需处理一次
                return result;

            } else if (node.type == TreeNode.Type.OR_GATE) {
                // 或门：纵向展开为多行
                for (TreeNode child : node.children) {
                    List<TreeNode> newPath = new ArrayList<>(path);
                    newPath.set(i, child);
                    result.add(newPath);
                }
                return result;
            }
        }
        return Collections.singletonList(path);
    }

    // 判断是否全为基本事件
    private static boolean isAllBasicEvents(List<TreeNode> path) {
        return path.stream().noneMatch(n -> n.type != TreeNode.Type.BASIC);
    }

    // 转换为基本事件集合
    private static Set<String> getBasicEventSet(List<TreeNode> path) {
        Set<String> set = new HashSet<>();
        path.forEach(n -> set.add(n.name));
        return set;
    }

    // 去除超集
    private static Set<Set<String>> removeSupersets(Set<Set<String>> sets) {
        Set<Set<String>> minimal = new HashSet<>();
        for (Set<String> candidate : sets) {
            boolean isMinimal = true;
            for (Set<String> existing : minimal) {
                if (candidate.containsAll(existing)) {
                    isMinimal = false;
                    break;
                }
            }
            if (isMinimal) {
                minimal.removeIf(s -> s.containsAll(candidate));
                minimal.add(new HashSet<>(candidate));
            }
        }
        return minimal;
    }

    // 示例用法
    public static void main(String[] args) {
        // 构建示例故障树：T = (X1 ∨ X2) ∧ (X3 ∧ X4)
        TreeNode x1 = new TreeNode(TreeNode.Type.BASIC, "X1");
        TreeNode x2 = new TreeNode(TreeNode.Type.BASIC, "X2");
        TreeNode x3 = new TreeNode(TreeNode.Type.BASIC, "X3");
        TreeNode x4 = new TreeNode(TreeNode.Type.BASIC, "X4");
        TreeNode x5 = new TreeNode(TreeNode.Type.BASIC, "X5");
        TreeNode x6 = new TreeNode(TreeNode.Type.BASIC, "X6");

        TreeNode orGate = new TreeNode(TreeNode.Type.OR_GATE, "OR");
        orGate.children.add(x1);
        orGate.children.add(x2);

        TreeNode andGate = new TreeNode(TreeNode.Type.AND_GATE, "AND");
        andGate.children.add(x3);
        andGate.children.add(x4);

        TreeNode root = new TreeNode(TreeNode.Type.AND_GATE, "T");
        root.children.add(orGate);
        root.children.add(andGate);

        // 计算并打印结果
        Set<Set<String>> minimalCutSets = calculateMinimalCutSets(root);
        System.out.println("min cut set:");
        minimalCutSets.forEach(System.out::println);


        // 多层嵌套示例：T = ((X1 ∧ X2) ∨ X3) ∧ (X4 ∨ (X5 ∧ X6))

        TreeNode innerAnd = new TreeNode(TreeNode.Type.AND_GATE, "AND1");
        innerAnd.children.add(x5);
        innerAnd.children.add(x6);

        TreeNode orGate2 = new TreeNode(TreeNode.Type.OR_GATE, "OR2");
        orGate2.children.add(x4);
        orGate2.children.add(innerAnd);

        TreeNode innerAnd2 = new TreeNode(TreeNode.Type.AND_GATE, "AND2");
        innerAnd2.children.add(x1);
        innerAnd2.children.add(x2);

        TreeNode orGate3 = new TreeNode(TreeNode.Type.OR_GATE, "OR3");
        orGate3.children.add(innerAnd2);
        orGate3.children.add(x3);

        TreeNode rootComplex = new TreeNode(TreeNode.Type.AND_GATE, "T");
        rootComplex.children.add(orGate3);
        rootComplex.children.add(orGate2);

        Set<Set<String>> minimalCutSets2 = calculateMinimalCutSets(rootComplex);

        // 计算并打印结果
        System.out.println("min cut set complex:");
        minimalCutSets2.forEach(System.out::println);

    }
}