高数下册笔记

关于高等数学下册的一些笔记

---

向量的方向角和方向余弦

向量叉乘

在三维几何中，向量a和向量b的叉乘结果是一个向量，该向量垂直于a和b向量构成的平面，该向量也被称作法向量

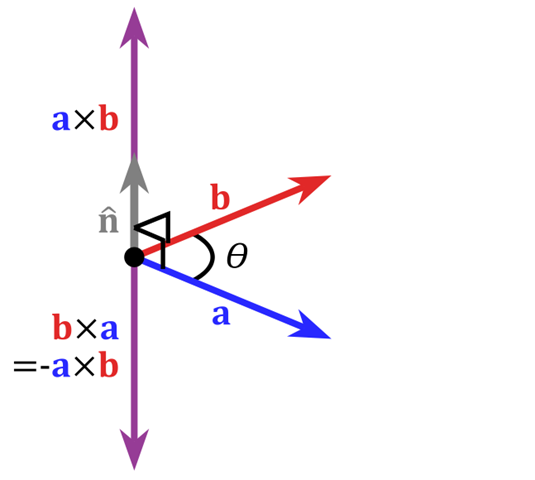
右手螺旋定则，手指指向左元。

叉乘公式

—行列式的展开

空间平面

空间平面方程

表达式

• 截距式

  $x/a+y/b+z/c=1$它与三坐标轴的交点分别为 $P(a,0,0),Q(0,b,0),R(0,0,c)$

• 点法式

  $A(x-x_0)+B(y-y_0)+C(z-z_0)=0$法向量为 $\vec{n}=(A,B,C)$

• 一般式

  $Ax+By+Cz+D=0$基本与点法式相同

可用平面上两条相交的直线的方向向量做点乘从而求出平面法向量

空间直线

空间直线方程

• 两平面联立
• 对称式，由方向向量和直线上一点确定
• 参数式 // 可由对称式导出

详情戳链接

空间曲面与空间曲线

空间曲面及其方程

曲线弧长

设空间曲线C由参数方程
$$x=x(t),y=y(t),z=z(t)$$

给出，且函数 $x=x(t),y=y(t),z=z(t)$ 在闭区间 $[\alpha ,\beta ]$ 上连续则弧长s为

$$s={\int }_{\alpha }^{\beta }\sqrt{x^{\prime 2}(t)+y^{\prime 2}(t)+z^{\prime 2}(t)}dt$$

曲线切面

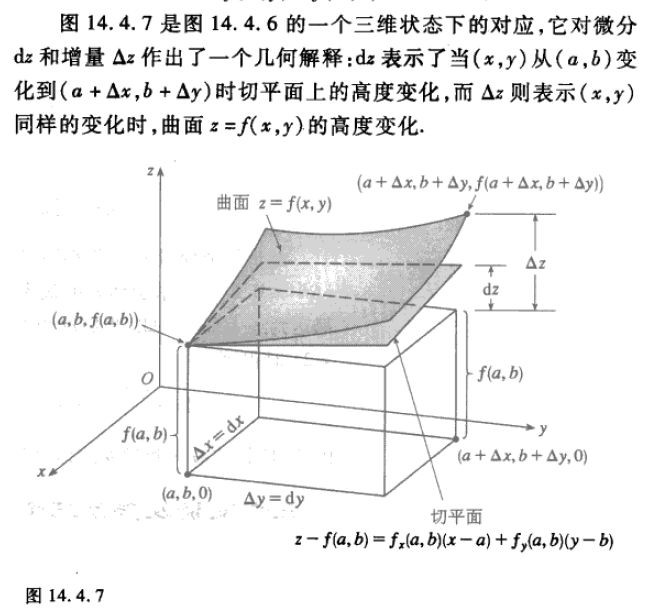
设空间曲面的方程为
$$F(x,y,z)=0,$$
而 $M(x_0,y_0,z_0)$ 是曲面 $\Sigma$ 上的一点.

• 法向量:
  $$(F_x^{\prime }(x_0,y_0,z_0),F_y^{\prime }(x_0,y_0,z_0),F_z^{\prime }(x_0,y_0,z_0)).$$

• 法线方程:
  $$\frac{x-x_0}{F_x^{\prime }(x_0,y_0,z_0)}=\frac{y-y_0}{F_y^{\prime }(x_0,y_0,z_0)}=\frac{z-z_0}{F_z^{\prime }(x_0,y_0,z_0)}$$

• 切平面方程:
  $$F_x^{\prime }(x_0,y_0,z_0)(x-x_0)+F_y^{\prime }(x_0,y_0,z_0)(y-y_0)+F_z^{\prime }(x_0,y_0,z_0)(z-z_0)=0.$$

空间曲面与曲线 - 知乎,

空间曲面的切平面和法线-知乎,

空间曲线的切线

空间曲线可视作两个曲面相交而成。

设曲线 $l$ 由面 $\alpha ,\beta$ 相交而成，

曲线 $l$ 在 $M(x_0,y_0,z_0)$ 处的切线可视作面 $\alpha ,\beta$ 在点 $M(x_0,y_0,z_0)$ 处的切平面的交线 (切平面就是过曲面该点切线集)

那么设面 $\alpha ,\beta$ 在 $M(x_0,y_0,z_0)$ 的法向量分别为 $n_1,n_2$ ，显然 $l=n_1\times n_2$.

• 面 $\alpha$ 的法向量：$$n_1=[\frac{\partial F}{\partial x},\frac{\partial F}{\partial y},\frac{\partial F}{\partial z}{]}^T$$ ，
• 面 $\beta$ 的法向量：$$n_2=[\frac{\partial G}{\partial x},\frac{\partial G}{\partial y},\frac{\partial G}{\partial z}{]}^T$$ 。
• 显然 $$n_1\times n_2=[\frac{\partial (F,G)}{\partial (y,z)},\frac{\partial (F,G)}{\partial (z,x)},\frac{\partial (F,G)}{\partial (x,y)}{]}^T$$.

其中 $\frac{\partial (F,G)}{\partial (x,y)}=\left|\begin{array}{cc}\frac{\partial F}{\partial x}& \frac{\partial F}{\partial y}\\ \frac{\partial G}{\partial x}& \frac{\partial G}{\partial y}\end{array}\right|$.

参考

空间曲面

切平面与法线

注记： 心中始终想着一个特例，球面：
$$x^2+y^2+z^2=R^2.$$

皮球放在地上，地面就是切平面，过切点于地面垂直的线就是法线.

多元函数微分

可微的必要条件

若函数 $z=f(x,y)$ 在点 $(x_0,y_0)$ 处可微，则 $z=f(x,y)$ 在点 $(x_0,y_0)$ 处存在对变量 $x$ 和 $y$ 的偏导数，且

$$dz{|}_{(x_0,y_0)}=f_x^{\prime }(x,y)\Delta x+f_y^{\prime }(x,y)\Delta y.$$

函数 $z=f(x,y)$ 在点 $(x_0,y_0)$ 处的全微分可表示为

$$dz{|}_{x_0,y_0}=f_x^{\prime }(x_0,y_0)dx+f_y^{\prime }(x_0,y_0)dy.$$

可微的充分条件

若函数 $z=f(x,y)$ 的两个偏导数在点 $(x_0,y_0)$ 的某邻域存在，且 $f_x^{\prime }(x,y)$ 与 $f_y^{\prime }(x,y)$ 在点 $(x_0,y_0)$ 处连续，则函数 $z=f(x,y)$ 在点 $(x_0,y_0)$ 处可微。

从公式出发
$$\Delta z=f_x^{\prime }(x_0,y_0)\Delta x+f_y^{\prime }(x_0,y_0)\Delta y+\alpha \Delta x+\beta \Delta y.$$

$$\rho =\sqrt{(\Delta x{)}^2+(\Delta y{)}^2}$$

若满足下式则称可微（即余项是 $\rho$ 的高阶无穷小

$$\underset{\rho \to 0}{\lim }\frac{\alpha \Delta x+\beta \Delta y}{\rho }=0.$$

偏微分（偏导）

若函数 $z=f(u,v)$ 可微，则称其全微分为
$$dz=\frac{\partial z}{\partial u}du+\frac{\partial z}{\partial v}dv$$

隐函数微分

• 二元
  $$y^{\prime }=-\frac{F_x^{\prime }(x,y)}{F_y^{\prime }(x,y)}.$$

• 三元

  设函数 $F(x,y,z)=0$

  有偏导

  • $F_x^{\prime }(x,y,z)$

  • $F_y^{\prime }(x,y,z)$

  • $F_z^{\prime }(x,y,z)$

    则有（注意负号）

  $$z_x^{\prime }=f_x^{\prime }(x,y)=-\frac{F_x^{\prime }(x,y,z)}{F_z^{\prime }(x,y,z)}$$

  $$z_y^{\prime }=f_y^{\prime }(x,y)=-\frac{F_y^{\prime }(x,y,z)}{F_z^{\prime }(x,y,z)}$$

雅可比行列式

多用于坐标系变换，在积分微元改变后要乘上雅可比行列式

参考:积分“秘宝”——雅克比行列式 - 古诚的文章 - 知乎,

多元函数极值

多元函数极值

必要条件： 设函数 $f(x,y)$ 在点 $M_0(x_0,y_0)$ 处存在偏导数，且取极值，则
$$f_x^{\prime }(x_0,y_0)=0,f_y^{\prime }(x_0,y_0)=0.$$
充分条件：设函数 $z=f(x,y)$ 在点 $M_0(x_0,y_0)$ 的某邻域 $U(M_0)$ 内具有二阶连续偏导数，$M_0$ 是 $f(x,y)$ 的驻点，记
$$A=f_{xx}^{\prime \prime }(x_0,y_0),B=f_{xy}^{\prime \prime }(x_0,y_0),C=f_{yy}^{\prime \prime }(x_0,y_0).$$

1. 若 $B^2-AC<0$ ，则 $M_0$ 是 $f(x,y)$ 的极值点. 且当 $A<0$ 时，$M_0$ 为极大值点；当 $A>0$ 时，$M_0$ 为极小值点.
2. 若 $B^2-AC>0$ , 则 $M_0$ 不是 $f(x,y)$ 的极值点.
   

条件极值

拉格朗日乘数法

方向导数和梯度

方向导数

设函数 $z=f(x,y)$ 在 $P_0(x_0,y_0)$ 点的某邻域内有定义，$\mathbf{l}$ 为 $xoy$ 坐标平面上的一个向量，$P(x,y)$ 是由 $P_0$ 点出发、方向为 $\mathbf{l}$ 的射线上的点，记 $\rho =\sqrt{(x-x_0{)}^2+(y-y_0{)}^2}$。 如果极限
$$\underset{\rho \to 0^{+}}{\lim }\frac{f(x,y)-f(x_0,y_0)}{\rho }$$
存在，则称函数 $f(x,y)$ 在 $P_0$ 点沿方向 $\mathbf{l}$ 的方向导数存在，并称此极限为函数 $f(x,y)$ 在 $P_0$ 点沿方向 $\mathbf{l}$ 的方向导数，记为
$$\frac{\partial z}{\partial \mathbf{l}}{|}_{P_0}或\frac{\partial f}{\partial \mathbf{l}}{|}_{P_0}，$$
即
$$\frac{\partial z}{\partial \mathbf{l}}{|}_{P_0}=\underset{\rho \to 0^{+}}{\lim }\frac{f(x,y)-f(x_0,y_0)}{\rho }.$$

计算
$$\frac{\partial z}{\partial \mathbf{l}}{|}_{P_0}=\frac{\partial z}{\partial x}{|}_{P_0}\cos \alpha +\frac{\partial z}{\partial y}{|}_{P_0}\cos \beta ,$$
其中$\cos \alpha ,\cos \beta$是 $\mathbf{l}$ 的方向余弦

若 $\mathbf{l}=(a,b,c)$则 $\mathbf{l}$ 的方向余弦为
$$\cos \alpha =\frac{a}{|\mathbf{l}|},\cos \beta =\frac{b}{|\mathbf{l}|},\cos \gamma =\frac{c}{|\mathbf{l}|}.$$

梯度

$${\mathbf{grad}u{|}_{P_0}=(\frac{\partial u}{\partial x},\frac{\partial u}{\partial y},\frac{\partial u}{\partial z})|}_{P_0}.$$